Leetcode-543. Diameter of Binary Tree

subject

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1: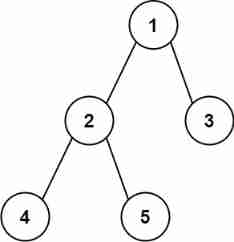

Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 104].
-100 <= Node.val <= 100

solution

Method 1 ： Depth-first search

First, we know that the length of a path is the number of nodes that the path passes through minus one , So find the diameter （ That is, find the maximum value of the path length ） Equivalent to finding the maximum number of nodes the path passes through minus one .

Any path can be regarded as starting from a node , From the stitching of the paths traversed downward by his left son and right son .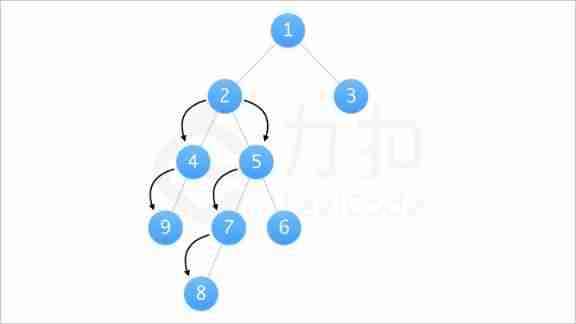

As shown in the figure, we can know the path [9, 4, 2, 5, 7, 8] Can be seen as 2 As a starting point , The path traversed down from his left son [2, 4, 9] And the path traversed down from his right son [2, 5, 7, 8] Spliced to get .

Suppose we know that the left son of the node traverses down the maximum number of nodes LL （ That is, the depth of the subtree with the left son as the root ） And its right son traverse down the maximum number of nodes R （ That is, the depth of the subtree with the right son as the root ）, Then the maximum number of nodes that the path starting from this node passes through is L+R+1 .

We remember the nodes node The maximum number of nodes passed by the path as the starting point is node, Then the diameter of the binary tree is all the nodes node Minus one... From the maximum .

The final algorithm flow is ： We define a recursive function depth(node) Calculation node, Function returns the depth of the subtree whose node is the root .

First, recursively call the left son and the right son to find the depth of the subtree with their roots LL and RR , Then the depth of the subtree whose node is the root is max(L,R)+1
Of this node d node The value is
L+R+1

Recursively search each node and set a global variable ans Record d node The maximum of , Finally back to ans-1 Is the diameter of the tree .

Code

/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
    
    int maxd = 0;
    public int diameterOfBinaryTree(TreeNode root) {
    
        getDepth(root);
        return maxd;
    }

    public int getDepth(TreeNode node){
    
        if(node == null){
    
            return 0;
        }

        int L,R;
        L = getDepth(node.left);
        R = getDepth(node.right);
        maxd = Math.max(L+R,maxd);
        return Math.max(L,R) + 1;
    }
}

Complexity analysis

Time complexity ：O(N), among NN Is the number of nodes in the binary tree , That is, the time complexity of traversing a binary tree , Each node is accessed only once .

Spatial complexity ：O(Height), among Height Is the height of the binary tree . Because the recursive function needs to allocate stack space for each layer of recursive function in the recursive process , So extra space is needed here, and that space depends on the depth of the recursion , The depth of recursion is obviously the height of binary tree , And each recursive call uses only constant variables , So the required space complexity is O(Height).

source

author ：LeetCode-Solution
link ：https://leetcode-cn.com/problems/diameter-of-binary-tree/solution/er-cha-shu-de-zhi-jing-by-leetcode-solution/
source ： Power button （LeetCode）
The copyright belongs to the author . Commercial reprint please contact the author for authorization , Non-commercial reprint please indicate the source .