当前位置:网站首页>(POJ - 3258) River hopper (two points)
(POJ - 3258) River hopper (two points)
2022-07-06 16:09:00 【AC__ dream】
Topic link :River Hopscotch - POJ 3258 - Virtual Judge
The question :
Every year cows hold various special versions of house jumping competitions , Including jumping from one rock to another in the river . This exciting activity is carried out in a long straight river , At start point and distance start point L There is a rock at the far end (1 ≤ L ≤ 10^9). Between the beginning and the end , Yes N A rock (0 ≤ N ≤ 50000), The distance between each rock and the starting point is Di (0 < Di < L).
In the course of the game , Cows take turns starting from the starting point , Try to reach the end , Each step can only jump from one rock to another . Of course , Weak cows cannot reach the finish line , He quit the race in the middle of the river .
Farmer John is proud of his cows and watches the race every year . But over time , Watching the timid cows of other farmers move slowly between the rocks close to each other , He felt very bored . He plans to remove some rocks , Make the process from the beginning to the end , The shortest jump distance is the longest , The distance from jumping to the end is not counted . He can remove at most... Except the beginning and the end M A rock (0 ≤ M ≤ N).
Please help farmer John make sure : After removing these rocks , What is the maximum value of the shortest jump distance ?
Input
The first 1 The line contains three integers separated by a single space L, N, M.
The first 2 To N + 1 That's ok , One integer per row , Represents the distance between each rock and the starting point . There won't be two rocks in the same place .
Output
Output an integer , That is, the maximum value of the shortest jump distance .
Sample input
25 5 2 2 14 11 21 17
Sample output
4
analysis : A simple analysis shows that the answer is monotonic , Now suppose that the number of stones we can remove is uncertain , That is to say, if the shortest jumping distance is x The number of stones to be removed is y, Then for any shortest jumping distance is u(u>x) The minimum number of stones to be removed in the scheme v Must be greater than or equal to y, So we can calculate the shortest distance according to this dichotomy , Each time, judge whether the shortest distance is larger or smaller by comparing the number of stones that need to be removed with the given number of stones that can be removed , The specific comparison method is as follows :
The shortest jumping distance is x The number of stones to be removed is y, if y<=m, In other words, we can increase the shortest distance by removing a few more stones , So is x Less than or equal to the correct answer , The opposite is greater than the correct answer
Attention to detail : When the shortest jumping distance is x The number of stones to be removed is y, if y=m, be x Not necessarily the answer , In fact, at this time x Is less than or equal to the correct answer
Here is the code :
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
const int N=5e4+10;
int a[N],n,m,L;
bool check(int x)
{
int cnt=0,r=0;// Record the minimum number of stones that need to be removed ,r For the position of the last stone
for(int i=1;i<=n+1;i++)
{
if(a[i]-r<x) cnt++;// Once the distance is less than x Then the stone will be removed
else r=a[i];
}
if(cnt<=m) return true;// The answer is too small
return false;
}
int main()
{
cin>>L>>n>>m;
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
a[n+1]=L;
sort(a+1,a+n+1);
int l=1e9+10,r=1e9+10,mid;
for(int i=1;i<=n+1;i++)
l=min(l,a[i]-a[i-1]);
while(l<r)
{
mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
printf("%d",l);
return 0;
}边栏推荐
- Information security - security professional name | CVE | rce | POC | Vul | 0day
- 渗透测试 ( 7 ) --- 漏洞扫描工具 Nessus
- Truck History
- D - function (HDU - 6546) girls' competition
- 渗透测试 ( 2 ) --- 渗透测试系统、靶机、GoogleHacking、kali工具
- [exercise -11] 4 values why sum is 0 (and 4 values of 0)
- Information security - threat detection - Flink broadcast stream broadcaststate dual stream merging application in filtering security logs
- [teacher Gao UML software modeling foundation] collection of exercises and answers for level 20 cloud class
- 2027. Minimum number of operations to convert strings
- Information security - threat detection - detailed design of NAT log access threat detection platform
猜你喜欢
![mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’](/img/e6/f4a696179282fe1f4193410c5a493a.png)
mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’
b站 實時彈幕和曆史彈幕 Protobuf 格式解析
Gartner:关于零信任网络访问最佳实践的五个建议

C language must memorize code Encyclopedia
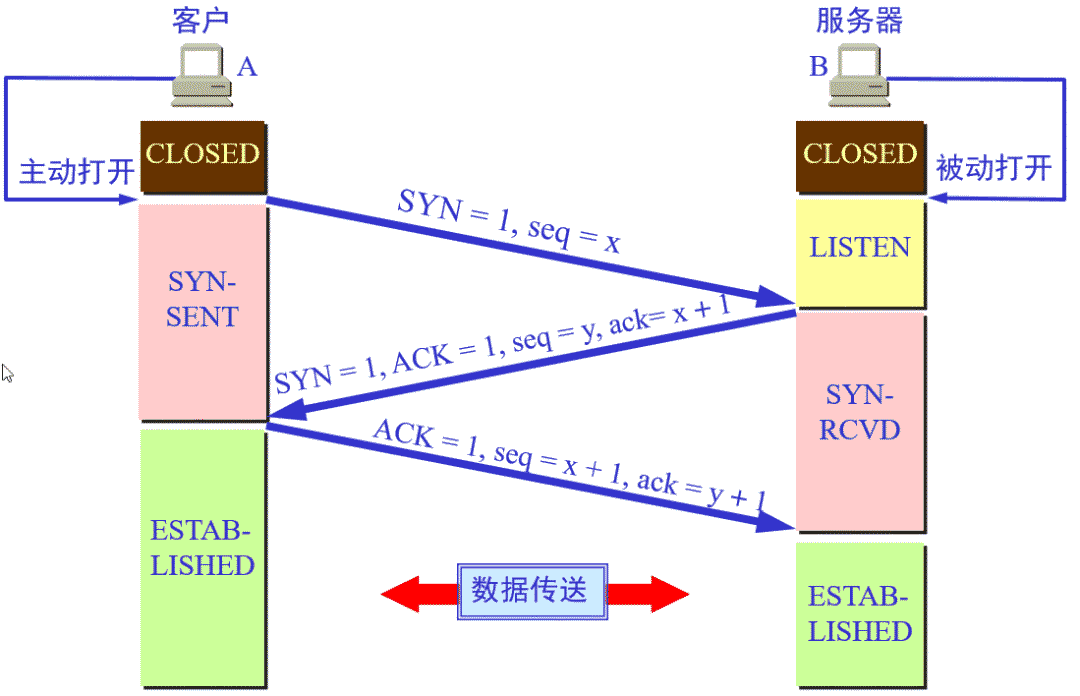
TCP's three handshakes and four waves
树莓派4B安装opencv3.4.0

C language is the watershed between low-level and high-level
Write web games in C language
渗透测试 ( 3 ) --- Metasploit Framework ( MSF )
Luogu P1102 A-B number pair (dichotomy, map, double pointer)
随机推荐
[exercise-7] (UVA 10976) fractions again?! (fraction split)
Data storage in memory & loading into memory to make the program run
Basic Q & A of introductory C language
基于web的照片数码冲印网站
D - function (HDU - 6546) girls' competition
Interesting drink
The most complete programming language online API document
Opencv learning log 12 binarization of Otsu method
1605. Sum the feasible matrix for a given row and column
【练习-11】4 Values whose Sum is 0(和为0的4个值)
【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
渗透测试 2 --- XSS、CSRF、文件上传、文件包含、反序列化漏洞
Opencv learning log 32 edge extraction
滲透測試 ( 1 ) --- 必備 工具、導航
TCP's three handshakes and four waves
Penetration test (4) -- detailed explanation of meterpreter command
1323. Maximum number of 6 and 9
2027. Minimum number of operations to convert strings
Research Report of cylindrical grinder industry - market status analysis and development prospect forecast
信息安全-史诗级漏洞Log4j的漏洞机理和防范措施