当前位置:网站首页>一文读懂简单查询代价估算
一文读懂简单查询代价估算
2022-07-06 06:32:00 【华为云开发者联盟】
摘要:查询引擎会在所有可行的查询访问路径中选择执行代价最低的一条。
本文分享自华为云社区《一文读懂简单查询代价估算【这次高斯不是数学家】》,作者: leapdb。
查询代价估算——如何选择一条最优的执行路径
SQL生命周期:词法分析(Lex) -> 语法分析(YACC) -> 分析重写 -> 查询优化(逻辑优化和物理优化) -> 查询计划生成 -> 查询执行。
- 词法分析:描述词法分析器的*.l文件经Lex工具编译生成lex.yy.c, 再由C编译器生成可执行的词法分析器。基本功能就是将一堆字符串根据设定的保留关键字和非保留关键字,转化成相应的标识符(Tokens)。
- 语法分析:语法规则描述文件*.y经YACC工具编译生成gram.c,再由C编译器生成可执行的语法分析器。基本功能就是将一堆标识符(Tokens)根据设定的语法规则,转化成原始语法树。
- 分析重写:查询分析将原始语法树转换为查询语法树(各种transform);查询重写根据pg_rewrite中的规则改写表和视图,最终得到查询语法树。
- 查询优化:经过逻辑优化和物理优化(生成最优路径)。
- 查询计划生成:将最优的查询路径转化为查询计划。
- 查询执行:通过执行器去执行查询计划生成查询的结果集。
在物理优化阶段,同样的一条SQL语句可以产生很多种查询路径,例如:多表JOIN操作,不同的JOIN顺序产生不同的执行路径,也导致中间结果元组规模的不同。查询引擎会在所有可行的查询访问路径中选择执行代价最低的一条。
通常我们依据 COST = COST(CPU) + COST(IO) 这一公式来选择最优执行计划。这里最主要的问题是如何确定满足某个条件的元组数量,基本方法就是依据统计信息和一定的统计模型。某条件的查询代价 = tuple_num * per_tuple_cost。
统计信息主要是pg_class中的relpages和reltuples,以及pg_statistics中的distinct, nullfrac, mcv, histgram等。
为何需要这些统计信息,有了这些够不够?
统计信息的收集来自analyze命令通过random方式随机采集的部分样本数据。我们将其转化为一个数学问题就是:给定一个常量数组可以分析出来哪些数据特征?找规律哈。
用最朴素的数学知识能想到的是:
- 是不是空数组
- 是不是常量数组
- 是不是unique无重复
- 是不是有序
- 是不是单调的,等差,等比
- 出现次数最多的数字有哪些
- 数据的分布规律(打点方式描绘数据增长趋势)
还有吗?这是一个值得不断思考的问题。
如何依据统计信息估算查询代价
统计信息是不准确的,不可靠的,两个原因:
- 统计信息只来自部分采样数据,不能精准描述全局特征。
- 统计信息是历史数据,实际数据随时可能在变化。
如何设计一个数学模型,利用不可靠的统计信息,尽可能准确的估算查询代价,是一个很有意思的事情。接下来我们通过一个个的具体例子来介绍。
主要内容来自以下链接,我们主要对其进行详细的解读。
PostgreSQL: Documentation: 14: Chapter 72. How the Planner Uses Statistics
PostgreSQL: Documentation: 14: 14.1. Using EXPLAIN
最简单的表的行数估算(使用relpages和reltuples)
SELECT relpages, reltuples FROM pg_class WHERE relname = 'tenk1'; ---采样估算有358个页面,10000条元组
relpages | reltuples
----------+-----------
358 | 10000
EXPLAIN SELECT * FROM tenk1; ---查询估算该表有10000条元组
QUERY PLAN
-------------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..458.00 rows=10000 width=244)【思考】查询计划中估算的rows=10000就直接是pg_class->reltuples吗?
统计信息是历史数据,表的元组数在随时变化。例如:analyze数据采样时有10个页面,存在50条元组;实际执行时有20个页面,可能存在多少条元组?用你最朴素的情感想一想是不是,很可能是100条元组对不对?
表大小的估算方法在函数 estimate_rel_size -> table_relation_estimate_size -> heapam_estimate_rel_size 中。
- 先通过表物理文件的大小计算实际页面数actual_pages = file_size / BLOCKSIZE
- 计算页面的元组密度
a. 如果relpages大于0,density = reltuples / (double) relpages
b. 如果relpages为空,density = (BLCKSZ - SizeOfPageHeaderData) / tuple_width, 页面大小 / 元组宽度。 - 估算表元组个数 = 页面元组密度 * 实际页面数 = density * actual_pages
所以,估算rows的10000 = (10000 / 358) * 358,历史页面密度 * 新的页面数,以推算当前元组数。
最简单的范围比较(使用直方图)
SELECT histogram_bounds FROM pg_stats WHERE tablename='tenk1' AND attname='unique1';
histogram_bounds
------------------------------------------------------
{0,993,1997,3050,4040,5036,5957,7057,8029,9016,9995}
EXPLAIN SELECT * FROM tenk1 WHERE unique1 < 1000; ---估算小于1000的有1007条
QUERY PLAN
--------------------------------------------------------------------------------
Bitmap Heap Scan on tenk1 (cost=24.06..394.64 rows=1007 width=244)
Recheck Cond: (unique1 < 1000)
-> Bitmap Index Scan on tenk1_unique1 (cost=0.00..23.80 rows=1007 width=0)
Index Cond: (unique1 < 1000)查询引擎在查询语法树的WHERE子句中识别出比较条件,再到pg_operator中根据操作符和数据类型找到oprrest为scalarltsel,这是通用的标量数据类型的小于操作符的代价估算函数。最终是在 scalarineqsel -> ineq_histogram_selectivity 中进行直方图代价估算。
在PG中采用的是等高直方图,也叫等频直方图。将样本范围划分成N等份的若干个子区间,取所有子区间的边界值,构成直方图。
使用:使用时认为子区间(也叫桶)内的值是线性单调分布的,也认为直方图的覆盖范围就是整个数据列的范围。因此,只需计算出在直方图中的占比,既是总体中的占比。
【思考】以上的两点假设靠谱吗?有没有更合理的办法?
选择率 = (前面桶的总数 + 目标值在当前桶中的范围 / 当前桶的区间范围) / 桶的总数
selectivity = (1 + (1000 - bucket[2].min) / (bucket[2].max - bucket[2].min)) / num_buckets
= (1 + (1000 - 993) / (1997 - 993)) / 10
= 0.100697
估算元组数 = 基表元组数 * 条件选择率
rows = rel_cardinality * selectivity
= 10000 * 0.100697
= 1007 (rounding off)最简单的等值比较(使用MCV)
SELECT null_frac, n_distinct, most_common_vals, most_common_freqs FROM pg_stats WHERE tablename='tenk1' AND attname='stringu1';
null_frac | 0
n_distinct | 676
most_common_vals | {EJAAAA,BBAAAA,CRAAAA,FCAAAA,FEAAAA,GSAAAA,JOAAAA,MCAAAA,NAAAAA,WGAAAA}
most_common_freqs | {0.00333333,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003}
EXPLAIN SELECT * FROM tenk1 WHERE stringu1 = 'CRAAAA'; ---
QUERY PLAN
----------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..483.00 rows=30 width=244)
Filter: (stringu1 = 'CRAAAA'::name)查询引擎在查询语法树的WHERE子句中识别出比较条件,再到pg_operator中根据操作符和数据类型找到oprrest为eqsel,这是通用的等值比较操作符的代价估算函数。最终是在 eqsel_internal -> var_eq_const 中进行MCV代价估算。
MCV是在样本中选取重复次数最多的前100个组成,并计算每个值在样本中的占比。使用时,就简单的认为这个占比就是在全局中的占比。
【思考】将样本中占比就这样简单的认为是在全局中的占比,这样合理吗?有没有更好的办法?
CRAAAA位于MCV中的第3项,占比是0.003
selectivity = mcf[3]
= 0.003
rows = 10000 * 0.003
= 30接下来,我们在看一个不在MCV中的等值比较。
EXPLAIN SELECT * FROM tenk1 WHERE stringu1 = 'xxx'; ---查找不存在于MCV中的值
QUERY PLAN
----------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..483.00 rows=15 width=244)
Filter: (stringu1 = 'xxx'::name)通常MCV用于等值比较,直方图用于范围比较。“不存在于MCV中的值”,认为它们共享“不存在于MCV中的概率”,即:选择率 = (1 - MCV概率总和) / (不在MCV中的值的distinct个数)。
【思考】这样判断不在MCV中的方法合理吗?有没有更好的方法?
selectivity = (1 - sum(mvf)) / (num_distinct - num_mcv)
= (1 - (0.00333333 + 0.003 + 0.003 + 0.003 + 0.003 + 0.003 +
0.003 + 0.003 + 0.003 + 0.003)) / (676 - 10)
= 0.0014559
rows = 10000 * 0.0014559
= 15 (rounding off)复杂一点的范围比较(同时使用MCV和直方图)
前面 unique < 1000 的例子,在 scalarineqsel 函数中只利用到了直方图,是因为unique列没有重复值,也就不存在MCV。下面我们用一个不是unique的普通列再看一下范围比较。
这个范围包括两部分,重复次数比较多的值(在MCV中) 和 重复次数比较少的值(覆盖在直方图里),又由于计算直方图时去掉了MCV的值,因此MCV和直方图互相独立可以联合使用。
SELECT null_frac, n_distinct, most_common_vals, most_common_freqs FROM pg_stats WHERE tablename='tenk1' AND attname='stringu1';
null_frac | 0
n_distinct | 676
most_common_vals | {EJAAAA,BBAAAA,CRAAAA,FCAAAA,FEAAAA,GSAAAA,JOAAAA,MCAAAA,NAAAAA,WGAAAA}
most_common_freqs | {0.00333333,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003}
SELECT histogram_bounds FROM pg_stats WHERE tablename='tenk1' AND attname='stringu1';
histogram_bounds
--------------------------------------------------------------------------------
{AAAAAA,CQAAAA,FRAAAA,IBAAAA,KRAAAA,NFAAAA,PSAAAA,SGAAAA,VAAAAA,XLAAAA,ZZAAAA}
EXPLAIN SELECT * FROM tenk1 WHERE stringu1 < 'IAAAAA'; ---查找一个不存在于MCV中的值
QUERY PLAN
------------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..483.00 rows=3077 width=244)
Filter: (stringu1 < 'IAAAAA'::name)小于IAAAAA的值在MCV中有前6个,因此把它们的frac累加起来,就是小于IAAAAA且重复次数较多的人的概率
selectivity = sum(relevant mvfs)
= 0.00333333 + 0.003 + 0.003 + 0.003 + 0.003 + 0.003
= 0.01833333还有一部分小于IAAAAA但重复次数较少的人的概率 可以通过直方图进行范围计算。前面使用unique1列进行等值比较时,因为unique约束列不存在MCV,只有直方图。因此,只计算在直方图中桶的覆盖占比就是选择率了。这里还要考虑落在 直方图中值的整体占比 histogram_fraction = 1 - sum(mcv_frac),直方图桶的覆盖占比 * 整个直方图整体占比就是在直方图中的选择率了。
selectivity = mcv_selectivity + histogram_selectivity * histogram_fraction
= 0.01833333 + ((2 + ('IAAAAA'-'FRAAAA')/('IBAAAA'-'FRAAAA')) / 10) * (1 - sum(mvfs))
= 0.01833333 + 0.298387 * 0.96966667
= 0.307669
rows = 10000 * 0.307669
= 3077 (rounding off)【思考】在这个特殊的例子中,从MCV中计算出来的选择率为0.01833333,远小于从直方图中计算出来的选择率0.28933593,是因为该列中数值分布的太平缓了(统计信息显示MCV中的这些值出现的频率比其他值要高,这可能是因为采样导致的错误)。在大多数存在明显重复值多的场景下,从MCV中计算出的选择率会比较明显,因为重复值的出现概率是比较准确的。
多条件联合查询的例子
EXPLAIN SELECT * FROM tenk1 WHERE unique1 < 1000 AND stringu1 = 'xxx';
QUERY PLAN
--------------------------------------------------------------------------------
Bitmap Heap Scan on tenk1 (cost=23.80..396.91 rows=1 width=244)
Recheck Cond: (unique1 < 1000)
Filter: (stringu1 = 'xxx'::name)
-> Bitmap Index Scan on tenk1_unique1 (cost=0.00..23.80 rows=1007 width=0)
Index Cond: (unique1 < 1000)多条件的选择率计算其实也很简单,就按条件本身的逻辑运算来。
两个条件是与的关系,属于互相独立事件,就相乘就可以了。
selectivity = selectivity(unique1 < 1000) * selectivity(stringu1 = 'xxx')
= 0.100697 * 0.0014559
= 0.0001466
rows = 10000 * 0.0001466
= 1 (rounding off)一个使用JOIN的例子
EXPLAIN SELECT * FROM tenk1 t1, tenk2 t2
WHERE t1.unique1 < 50 AND t1.unique2 = t2.unique2;
QUERY PLAN
--------------------------------------------------------------------------------------
Nested Loop (cost=4.64..456.23 rows=50 width=488)
-> Bitmap Heap Scan on tenk1 t1 (cost=4.64..142.17 rows=50 width=244)
Recheck Cond: (unique1 < 50)
-> Bitmap Index Scan on tenk1_unique1 (cost=0.00..4.63 rows=50 width=0)
Index Cond: (unique1 < 50)
-> Index Scan using tenk2_unique2 on tenk2 t2 (cost=0.00..6.27 rows=1 width=244)
Index Cond: (unique2 = t1.unique2)unique1 < 50这个约束在nested-loop join之前被执行,还是使用直方图计算,类似前面的简单范围查找的例子,只不过这次50落在第一个桶中。
selectivity = (0 + (50 - bucket[1].min)/(bucket[1].max - bucket[1].min))/num_buckets
= (0 + (50 - 0)/(993 - 0))/10
= 0.005035
rows = 10000 * 0.005035
= 50 (rounding off)JOIN约束t1.unique2 = t2.unique2的选择率估算,还是先到pg_operator中查找“等于”操作符的oprjoin,是eqjoinsel。JOIN的话,两边的统计信息都要参考。
SELECT tablename, null_frac,n_distinct, most_common_vals FROM pg_stats
WHERE tablename IN ('tenk1', 'tenk2') AND attname='unique2';
tablename | null_frac | n_distinct | most_common_vals
-----------+-----------+------------+------------------
tenk1 | 0 | -1 |
tenk2 | 0 | -1 |对于unique列没有MCV,所以这里我们只能依赖distinct和nullfrac来计算选择率。
【*】选择率 = 两边的非空概率相乘,再除以最大JOIN条数。
selectivity = (1 - null_frac1) * (1 - null_frac2) * min(1/num_distinct1, 1/num_distinct2)
= (1 - 0) * (1 - 0) / max(10000, 10000)
= 0.0001
【*】JOIN的函数估算就是两边输入数量的笛卡尔积,再乘以选择率
rows = (outer_cardinality * inner_cardinality) * selectivity
= (50 * 10000) * 0.0001
= 50如果存在MCV,则分成两部分计算选择率:在MCV中的部分和不在MCV中的部分。
更详细的信息
表大小的估算:src/backend/optimizer/util/plancat.c
一般逻辑子句的选择率估算:src/backend/optimizer/path/clausesel.c
操作符函数的选择率估算:src/backend/utils/adt/selfuncs.c.
边栏推荐
- Delete external table source data
- LeetCode每日一题(971. Flip Binary Tree To Match Preorder Traversal)
- MFC dynamically creates dialog boxes and changes the size and position of controls
- Thesis abstract translation, multilingual pure human translation
- The whole process realizes the single sign on function and the solution of "canceltoken" of undefined when the request is canceled
- Leetcode daily question (1997. first day where you have been in all the rooms)
- Simulation volume leetcode [general] 1314 Matrix area and
- 专业论文翻译,英文摘要如何写比较好
- [ 英语 ] 语法重塑 之 英语学习的核心框架 —— 英语兔学习笔记(1)
- leetcode 24. Exchange the nodes in the linked list in pairs
猜你喜欢
云服务器 AccessKey 密钥泄露利用
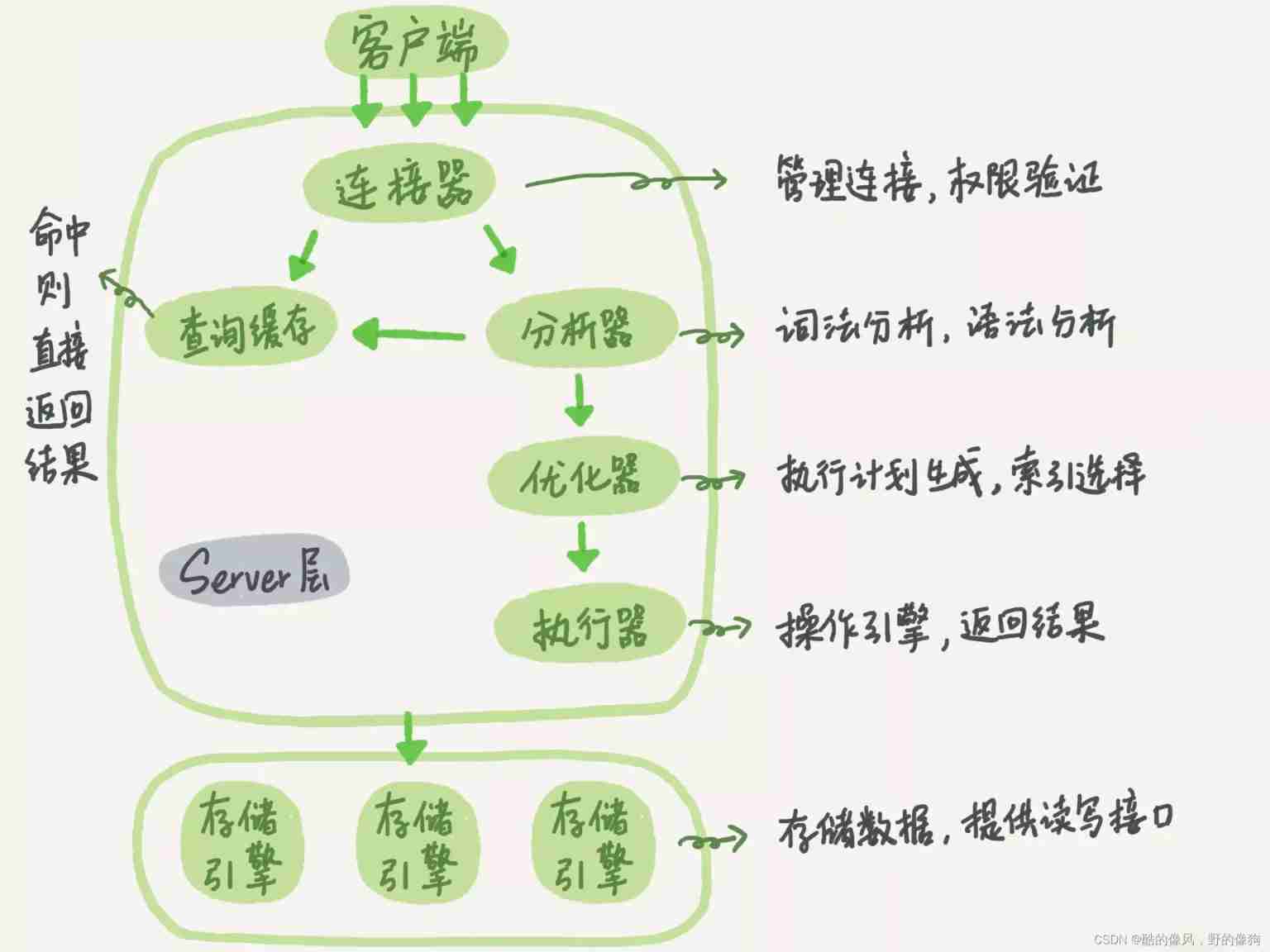
Advanced MySQL: Basics (1-4 Lectures)

生物医学英文合同翻译,关于词汇翻译的特点
Private cloud disk deployment

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
On the first day of clock in, click to open a surprise, and the switch statement is explained in detail
Transfert des paramètres de la barre d'adresse de la page de liste basée sur jeecg - boot
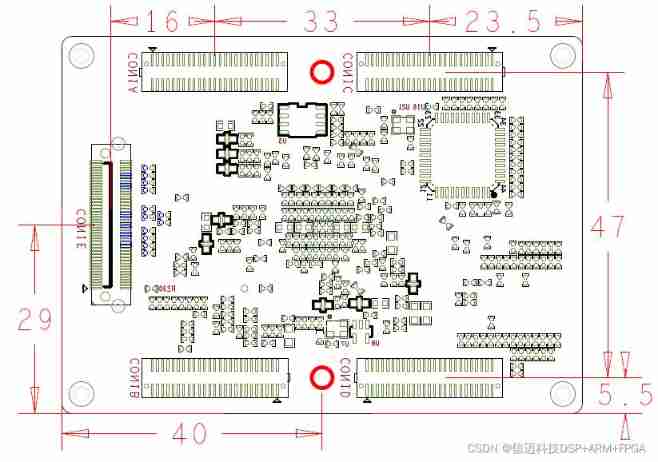
Tms320c665x + Xilinx artix7 DSP + FPGA high speed core board
![[web security] nodejs prototype chain pollution analysis](/img/b6/8eddc9cbe343f2439da92bf342b0dc.jpg)
[web security] nodejs prototype chain pollution analysis
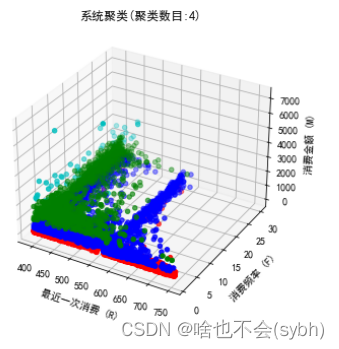
基于购买行为数据对超市顾客进行市场细分(RFM模型)
随机推荐
利用快捷方式-LNK-上线CS
Financial German translation, a professional translation company in Beijing
My seven years with NLP
MySQL is sorted alphabetically
Chinese English comparison: you can do this Best of luck
org.activiti.bpmn.exceptions.XMLException: cvc-complex-type.2.4.a: 发现了以元素 ‘outgoing‘ 开头的无效内容
SQL Server manager studio(SSMS)安装教程
oscp raven2靶机渗透过程
MySQL5.72. MSI installation failed
记一个基于JEECG-BOOT的比较复杂的增删改功能的实现
Simulation volume leetcode [general] 1447 Simplest fraction
Black cat takes you to learn UFS protocol Chapter 18: how UFS configures logical units (Lu Management)
基于JEECG-BOOT的list页面的地址栏参数传递
記一個基於JEECG-BOOT的比較複雜的增删改功能的實現
CS certificate fingerprint modification
国际经贸合同翻译 中译英怎样效果好
[Tera term] black cat takes you to learn TTL script -- serial port automation skill in embedded development
mysql按照首字母排序
Modify the list page on the basis of jeecg boot code generation (combined with customized components)
Mise en œuvre d’une fonction complexe d’ajout, de suppression et de modification basée sur jeecg - boot