当前位置:网站首页>信息與熵,你想知道的都在這裏了
信息與熵,你想知道的都在這裏了
2022-07-05 09:02:00 【aelum】
️ 本文參考自 [d2l] Information Theory
如果這篇文章有幫助到你,可以關注️ + 點贊 + 收藏 + 留言,您的支持將是我創作的最大動力
此外,本文所提到的 log ( ⋅ ) \log(\cdot) log(⋅) 如無特殊說明均指 log 2 ( ⋅ ) \log_2(\cdot) log2(⋅)。
目錄
一、自信息(Self-information)
先來看一個例子。擲一個質地均勻的骰子,會有 6 6 6 種可能的結果,且每種結果發生的概率均為 1 / 6 1/6 1/6。現在:
- 設事件 X = { 點數不大於 6 } X=\{\text{點數不大於}6\} X={ 點數不大於6},則顯然 P ( X ) = 1 \mathbb{P}(X)=1 P(X)=1;此外,這句話是廢話,它並沒有告訴我們任何信息,因為擲一個骰子得到的點數肯定不會超過 6 6 6;
- 設事件 X = { 點數不大於 5 } X=\{\text{點數不大於}5\} X={ 點數不大於5},則顯然 P ( X ) = 5 / 6 \mathbb{P}(X)=5/6 P(X)=5/6;此外,這句話包含了一些信息,但並不多,因為我們差不多能够猜到結果;
- 設事件 X = { 點數正好等於 2 } X=\{\text{點數正好等於}2\} X={ 點數正好等於2},則顯然 P ( X ) = 1 / 6 \mathbb{P}(X)=1/6 P(X)=1/6;此外,這句話的信息量要比上面那句話更大,因為 { 點數正好等於 2 } \{\text{點數正好等於}2\} { 點數正好等於2} 包含了 { 點數不大於 5 } \{\text{點數不大於}5\} { 點數不大於5} 的信息在裏面。
從這個例子可以看出,一個事件 X X X 所包含的信息量和它發生的概率有關系。概率越小信息量越大,概率越大信息量越少。
設事件 X X X 所包含的信息量為 I ( X ) I(X) I(X),其發生的概率為 p ≜ P ( X ) p\triangleq \mathbb{P}(X) p≜P(X),那麼我們如何尋找 I ( X ) I(X) I(X) 與 p p p 之間的關系呢?
首先,我們有以下常識:
- 觀測一個幾乎確定的事件得到的信息量幾乎是 0 0 0;
- 共同觀測兩個隨機變量得到的信息量不超過分別觀測兩個隨機變量得到的信息量的和,且該不等式取等當且僅當兩個隨機變量相互獨立。
設事件 X = { A 與 B 同 時 發 生 , 其 中 A 、 B 相 互 獨 立 } X=\{A與B同時發生,其中A、B相互獨立\} X={ A與B同時發生,其中A、B相互獨立},則顯然 P ( X ) = P ( A ) P ( B ) \mathbb{P}(X)=\mathbb{P}(A)\mathbb{P}(B) P(X)=P(A)P(B),而根據上述常識,又有 I ( X ) = I ( A ) + I ( B ) I(X)=I(A)+I(B) I(X)=I(A)+I(B)。不妨設 I ( ∗ ) = f ( P ( ∗ ) ) I(*)=f(\mathbb{P}(*)) I(∗)=f(P(∗)),則
f ( P ( A ) ⋅ P ( B ) ) = f ( P ( X ) ) = I ( X ) = I ( A ) + I ( B ) = f ( P ( A ) ) + f ( P ( B ) ) f(\mathbb{P}(A)\cdot \mathbb{P}(B))=f(\mathbb{P}(X))=I(X)=I(A)+I(B)=f(\mathbb{P}(A))+f(\mathbb{P}(B)) f(P(A)⋅P(B))=f(P(X))=I(X)=I(A)+I(B)=f(P(A))+f(P(B))
不難看出 log ( ⋅ ) \log(\cdot) log(⋅) 能够滿足這一要求。但考慮到 log x \log x logx 在 ( 0 , 1 ] (0,1] (0,1] 上是非正的且單調遞增,所以我們一般采用 − log ( ⋅ ) -\log(\cdot) −log(⋅) 來衡量一個事件的信息量。
綜合以上,設事件 X X X 發生的概率為 p p p,則其信息量(又稱自信息)可以這樣計算:
I ( X ) = − log p (1) \textcolor{red}{I(X)=-\log p\tag{1}} I(X)=−logp(1)
- 當 ( 1 ) (1) (1) 式中的 log \log log 以 2 2 2 為底時,自信息的單比特是 bit \text{bit} bit;
- 當 ( 1 ) (1) (1) 式中的 log \log log 以 e e e 為底時,自信息的單比特是 nat \text{nat} nat;
- 當 ( 1 ) (1) (1) 式中的 log \log log 以 10 10 10 為底時,自信息的單比特是 hart \text{hart} hart。
還可以得到:
1 nat = log 2 e bit ≈ 1.443 bit , 1 hart = log 2 10 bit ≈ 3.322 bit 1\;\text{nat}=\log_2 e\;\text{bit}\approx 1.443 \;\text{bit},\quad 1\;\text{hart}=\log_2 10\;\text{bit}\approx 3.322 \;\text{bit} 1nat=log2ebit≈1.443bit,1hart=log210bit≈3.322bit
我們知道,對於任何長度為 n n n 的二進制序列,它包含 n n n 比特的信息。例如,對於序列 0010 0010 0010,它出現的概率是 1 / 2 4 1/2^4 1/24,因此
I ( “ 0010 ” ) = − log 1 2 4 = 4 bits I(\text{“\,0010\,”})=-\log\frac{1}{2^4}=4\;\text{bits} I(“0010”)=−log241=4bits
二、熵(Entropy)
設隨機變量 X X X 服從分布 D \mathcal{D} D,則 X X X 的熵定義為其信息量的期望:
H ( X ) = E X ∼ D [ I ( X ) ] (2) \textcolor{red}{H(X)=\mathbb{E}_{X\sim\mathcal{D}}[I(X)]}\tag{2} H(X)=EX∼D[I(X)](2)
若 X X X 是離散分布,則
H ( X ) = − E X ∼ D [ log p i ] = − ∑ i p i log p i H(X)=-\mathbb{E}_{X\sim\mathcal{D}}[\log p_i]=-\sum_ip_i\log p_i H(X)=−EX∼D[logpi]=−i∑pilogpi
若 X X X 是連續分布,則
H ( X ) = − E X ∼ D [ log p ( x ) ] = − ∫ p ( x ) log p ( x ) d x H(X)=-\mathbb{E}_{X\sim\mathcal{D}}[\log p(x)]=-\int p(x)\log p(x)\text{d}x H(X)=−EX∼D[logp(x)]=−∫p(x)logp(x)dx
在離散情况下,設 X X X 只取 k k k 個值,則有: 0 ≤ H ( X ) ≤ log k 0\leq H(X)\leq \log k 0≤H(X)≤logk。
與信息量不同的是,這裏的 X X X 是隨機變量而不是事件
把事件看成一個點,則信息量可以看成一個點所產生的的信息,而信息熵則代錶一系列點所產生的信息的均量
接下來的章節中我們都將只討論離散情形,連續情形下的公式可類比推理
2.1 聯合熵(Joint Entropy)
我們已經知道如何計算 X X X 的信息熵了,那麼如何計算 ( X , Y ) (X,Y) (X,Y) 的信息熵呢?
設 ( X , Y ) ∼ D (X,Y)\sim\mathcal{D} (X,Y)∼D,聯合概率分布為 p i j ≜ P ( X = x i , Y = y j ) p_{ij}\triangleq \mathbb{P}(X=x_i,Y=y_j) pij≜P(X=xi,Y=yj),再記 p i = P ( X = x i ) , p j = P ( Y = y j ) p_i=\mathbb{P}(X=x_i),\,p_j=\mathbb{P}(Y=y_j) pi=P(X=xi),pj=P(Y=yj),依照信息熵的定義類似可得
H ( X , Y ) = − ∑ i j p i j log p i j (3) \textcolor{red}{H(X,Y)=-\sum_{ij}p_{ij}\log p_{ij}}\tag{3} H(X,Y)=−ij∑pijlogpij(3)
如果 X = Y X=Y X=Y,則 H ( X , Y ) = H ( X ) = H ( Y ) H(X,Y)=H(X)=H(Y) H(X,Y)=H(X)=H(Y);如果 X X X 和 Y Y Y 相互獨立,則 p i j = p i ⋅ p j p_{ij}=p_i\cdot p_j pij=pi⋅pj,進而
H ( X , Y ) = − ∑ i j ( p i ⋅ p j ) ( log p i + log p j ) = − ∑ j p j ∑ i p i log p i − ∑ i p i ∑ j p j log p j = H ( X ) + H ( Y ) H(X,Y)=-\sum_{ij}(p_i\cdot p_j)(\log p_i+\log p_j)=-\sum_j p_j\sum_i p_i\log p_i-\sum_ip_i\sum_jp_j\log p_j=H(X)+H(Y) H(X,Y)=−ij∑(pi⋅pj)(logpi+logpj)=−j∑pji∑pilogpi−i∑pij∑pjlogpj=H(X)+H(Y)
此外,總有以下不等式成立:
H ( X ) , H ( Y ) ≤ H ( X , Y ) ≤ H ( X ) + H ( Y ) H(X),H(Y)\leq H(X,Y)\leq H(X)+H(Y) H(X),H(Y)≤H(X,Y)≤H(X)+H(Y)
2.2 條件熵(Conditional Entropy)
條件熵 H ( Y ∣ X ) H(Y|X) H(Y∣X) 錶示在已知隨機變量 X X X 的情况下隨機變量 Y Y Y 的不確定性,定義為 X X X 給定條件下 Y Y Y 的條件概率分布的熵對 X X X 的數學期望:
H ( Y ∣ X ) = ∑ i p i H ( Y ∣ X = x i ) = ∑ i p i ( − ∑ j p j ∣ i log p j ∣ i ) = − ∑ i j p i j log p j ∣ i (4) H(Y|X)=\sum_i p_iH(Y|X=x_i)=\sum_i p_i \left( -\sum_j p_{j|i}\log p_{j|i}\right)=-\sum_{ij}p_{ij}\log p_{j|i}\tag{4} H(Y∣X)=i∑piH(Y∣X=xi)=i∑pi(−j∑pj∣ilogpj∣i)=−ij∑pijlogpj∣i(4)
利用 p j ∣ i = p i j / p i p_{j|i}=p_{ij}/p_i pj∣i=pij/pi 可得
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)
從上式可以看出, H ( Y ∣ X ) H(Y|X) H(Y∣X) 實際上代錶了包含在 Y Y Y 但不包含在 X X X 中的信息(類似於 P ( B \ A ) = P ( A ∪ B ) − P ( A ) \mathbb{P}(B\backslash A)=\mathbb{P}(A\cup B)-\mathbb{P}(A) P(B\A)=P(A∪B)−P(A))。
2.3 互信息(Mutual Information)
給定隨機變量 ( X , Y ) (X,Y) (X,Y),我們已經知道了 X X X 的信息可以用 H ( X ) H(X) H(X) 來錶示; ( X , Y ) (X,Y) (X,Y) 總共的信息可以用 H ( X , Y ) H(X,Y) H(X,Y) 來錶示;包含在 Y Y Y 但不包含在 X X X 中的信息可以用 H ( Y ∣ X ) H(Y|X) H(Y∣X) 來錶示。那我們該用什麼來衡量 X X X 和 Y Y Y 都包含的信息呢?
答案是互信息,其定義如下(可以理解為集合 X X X 與 Y Y Y 的交集):
I ( X , Y ) = H ( X , Y ) − H ( Y ∣ X ) − H ( X ∣ Y ) (5) \textcolor{red}{I(X,Y)=H(X,Y)-H(Y|X)-H(X|Y)}\tag{5} I(X,Y)=H(X,Y)−H(Y∣X)−H(X∣Y)(5)
熵、聯合熵、條件熵、互信息之間的關系如下:
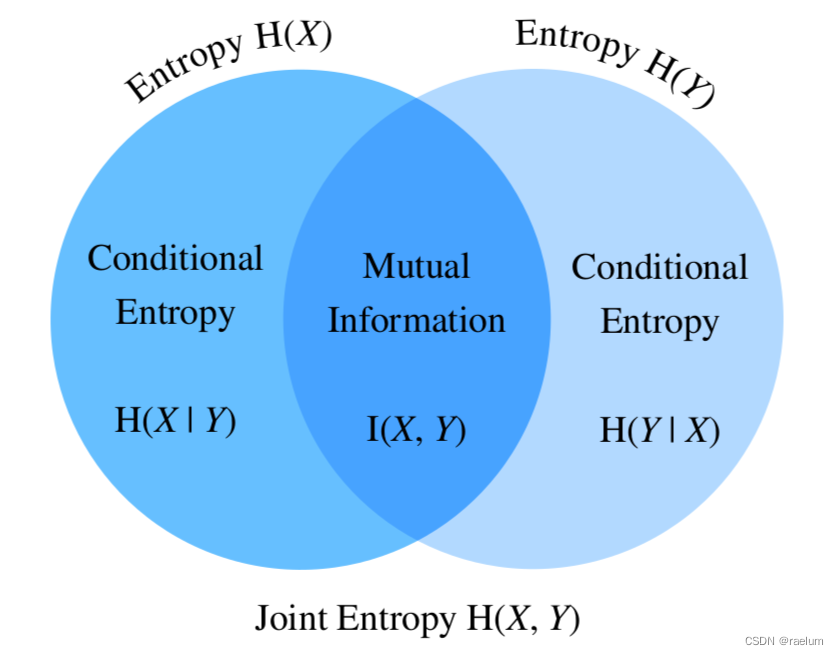
從上圖還可以得到:
I ( X , Y ) = H ( X ) − H ( X ∣ Y ) I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) \begin{aligned} I(X,Y)&=H(X)-H(X|Y) \\ I(X,Y)&=H(Y)-H(Y|X) \\ I(X,Y)&=H(X)+H(Y)-H(X,Y) \end{aligned} I(X,Y)I(X,Y)I(X,Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)
我們將 ( 5 ) (5) (5) 式展開得到
I ( X , Y ) = − ∑ i j p i j log p i j + ∑ i j p i j log p j ∣ i + ∑ i j p i j log p i ∣ j = ∑ i j p i j ( log p j ∣ i + log p i ∣ j − log p i j ) = ∑ i j p i j log p i j p i ⋅ p j = E ( X , Y ) ∼ D [ log p i j p i ⋅ p j ] \begin{aligned} I(X,Y)&=-\sum_{ij}p_{ij}\log p_{ij}+\sum_{ij}p_{ij}\log p_{j|i}+\sum_{ij}p_{ij}\log p_{i|j} \\ &=\sum_{ij}p_{ij}(\log p_{j|i}+\log p_{i|j}-\log p_{ij}) \\ &=\sum_{ij} p_{ij} \log \frac{p_{ij}}{p_i\cdot p_j} \\ &=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\left[\log \frac{p_{ij}}{p_i\cdot p_j}\right] \end{aligned} I(X,Y)=−ij∑pijlogpij+ij∑pijlogpj∣i+ij∑pijlogpi∣j=ij∑pij(logpj∣i+logpi∣j−logpij)=ij∑pijlogpi⋅pjpij=E(X,Y)∼D[logpi⋅pjpij]
互信息的一些性質:
- 對稱性: I ( X , Y ) = I ( Y , X ) I(X,Y)=I(Y,X) I(X,Y)=I(Y,X);
- 非負性: I ( X , Y ) ≥ 0 I(X,Y)\geq 0 I(X,Y)≥0;
- I ( X , Y ) = 0 I(X,Y)=0 I(X,Y)=0 ⇔ \;\Leftrightarrow\; ⇔ X X X 與 Y Y Y 相互獨立;
2.4 點互信息(Pointwise Mutual Information)
點互信息定義為:
PMI ( x i , y j ) = log p i j p i ⋅ p j (6) \textcolor{red}{\text{PMI}(x_i,y_j)=\log \frac{p_{ij}}{p_i\cdot p_j}} \tag{6} PMI(xi,yj)=logpi⋅pjpij(6)
結合 2.3 節,我們會發現有如下關系成立(好比信息熵是信息量的期望一樣,互信息也是點互信息的期望)
I ( X , Y ) = E ( X , Y ) ∼ D [ PMI ( x i , y j ) ] I(X,Y)=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\left[\text{PMI}(x_i,y_j)\right] I(X,Y)=E(X,Y)∼D[PMI(xi,yj)]
PMI 的值越高,錶示 x i x_i xi 與 y j y_j yj 的相關性越强。PMI 常用於 NLP 任務中計算兩個單詞之間的相關性,但如果語料庫不足,可能會出現 p i j = 0 p_{ij}=0 pij=0 的情况,這就導致兩個單詞的互信息為 − ∞ -\infty −∞,因此需要做一個修正:
PPMI ( x i , y j ) = max ( 0 , PMI ( x i , y j ) ) \text{PPMI}(x_i,y_j)=\max(0,\text{PMI}(x_i,y_j)) PPMI(xi,yj)=max(0,PMI(xi,yj))
上述的 PPMI 又稱為正點互信息(Positive PMI)。
三、相對熵(KL散度)
相對熵(Relative Entropy)又稱為KL散度(Kullback–Leibler divergence),後者是其更常用的名字。
設隨機變量 X X X 服從概率分布 P P P,現在我們嘗試用另外一個概率分布 Q Q Q 來估計 P P P(假設 Y ∼ Q Y\sim Q Y∼Q)。記 p i = P ( X = x i ) , q i = P ( Y = x i ) p_i=\mathbb{P}(X=x_i),\,q_i=\mathbb{P}(Y=x_i) pi=P(X=xi),qi=P(Y=xi),則KL散度定義為
D KL ( P ∥ Q ) = E X ∼ P [ log p i q i ] = ∑ i p i log p i q i (7) D_{\text{KL}}(P\Vert Q)=\mathbb{E}_{X\sim P}\left[\log \frac{p_i}{q_i}\right]=\sum_ip_i\log \frac{p_i}{q_i}\tag{7} DKL(P∥Q)=EX∼P[logqipi]=i∑pilogqipi(7)
KL散度的一些性質:
- 非對稱性: D KL ( P ∥ Q ) ≠ D KL ( Q ∥ P ) D_{\text{KL}}(P\Vert Q)\neq D_{\text{KL}}(Q\Vert P) DKL(P∥Q)=DKL(Q∥P);
- 非負性: D KL ( P ∥ Q ) ≥ 0 D_{\text{KL}}(P\Vert Q)\geq 0 DKL(P∥Q)≥0,等式成立當且僅當 P = Q P=Q P=Q;
- 若存在 x i x_i xi 使得 p i > 0 , q i = 0 p_i>0,\,q_i=0 pi>0,qi=0,則 D KL ( P ∥ Q ) = ∞ D_{\text{KL}}(P\Vert Q) =\infty DKL(P∥Q)=∞。
KL散度被用來衡量兩個概率分布之間的差异。如果兩個分布完全相等,則KL散度為 0 0 0。因此,KL散度可以用作多分類任務的損失函數。
由於KL散度不滿足對稱性,因此它不是嚴格意義上的 “距離”
四、交叉熵(Cross-Entropy)
我們將 ( 7 ) (7) (7) 式拆解
D KL ( P ∥ Q ) = ∑ i p i log p i − ∑ i p i log q i D_{\text{KL}}(P\Vert Q)=\sum_i p_i\log p_i-\sum_i p_i\log q_i DKL(P∥Q)=i∑pilogpi−i∑pilogqi
若令 CE ( P , Q ) = − ∑ i p i log q i \text{CE}(P,Q)=-\sum_i p_i\log q_i CE(P,Q)=−∑ipilogqi,則上式可寫成
D KL ( P ∥ Q ) = CE ( P , Q ) − H ( P ) D_{\text{KL}}(P\Vert Q)=\text{CE}(P,Q)-H(P) DKL(P∥Q)=CE(P,Q)−H(P)
而 CE ( P , Q ) \text{CE}(P,Q) CE(P,Q) 就是我們所說的交叉熵,其正式定義為
CE ( P , Q ) = − E X ∼ P [ log q i ] (8) \textcolor{red}{\text{CE}(P,Q)=-\mathbb{E}_{X\sim P}[\log q_i]}\tag{8} CE(P,Q)=−EX∼P[logqi](8)
結合KL散度的非負性,我們還可以得到 CE ( P , Q ) ≥ H ( P ) \text{CE}(P,Q)\geq H(P) CE(P,Q)≥H(P),該不等式又稱為吉布斯不等式。
通常 CE ( P , Q ) \text{CE}(P,Q) CE(P,Q) 也會寫成 H ( P , Q ) H(P,Q) H(P,Q)
交叉熵計算一例:
P P P 是真實分布,而 Q Q Q 是估計分布,考慮三分類問題,對於某個樣本,其真實標簽和預測結果列在下錶中:
| 類別 1 | 類別 2 | 類別 3 | |
|---|---|---|---|
| target | 0 | 1 | 0 |
| prediction | 0.2 | 0.7 | 0.1 |
從上錶可以看出,該樣本真實情况是屬於類別 2,且 p 1 = 0 , p 2 = 1 , p 3 = 0 , q 1 = 0.2 , q 2 = 0.7 , q 3 = 0.1 p_1=0,p_2=1,p_3=0,q_1=0.2,q_2=0.7,q_3=0.1 p1=0,p2=1,p3=0,q1=0.2,q2=0.7,q3=0.1。
因此
CE ( P , Q ) = − ( 0 ⋅ log 0.2 + 1 ⋅ log 0.7 + 0 ⋅ log 0.1 ) = − log 0.7 ≈ 0.5146 \text{CE}(P,Q)=-(0\cdot \log 0.2+1\cdot \log 0.7+0\cdot \log 0.1)=-\log 0.7\approx 0.5146 CE(P,Q)=−(0⋅log0.2+1⋅log0.7+0⋅log0.1)=−log0.7≈0.5146
當給定了數據集, H ( P ) H(P) H(P) 就成了一個常數,因此KL散度和交叉熵都能够用作多分類問題的損失函數。當真實分布 P P P 是 One-Hot 向量時,則有 H ( P ) = 0 H(P)=0 H(P)=0,此時交叉熵等於KL散度
4.1 二元交叉熵(Binary Cross-Entropy)
二元交叉熵(BCE)是交叉熵的一個特例
BCE ( P , Q ) = − ∑ i = 1 2 p i log q i = − ( p 1 log q 1 + p 2 log q 2 ) = − ( p 1 log q 1 + ( 1 − p 1 ) log ( 1 − q 1 ) ) \begin{aligned} \text{BCE}(P,Q)&=-\sum_{i=1}^2p_i\log q_i \\ &=-(p_1\log q_1+p_2\log q_2) \\ &=-(p_1\log q_1+(1-p_1)\log (1-q_1))\qquad \end{aligned} BCE(P,Q)=−i=1∑2pilogqi=−(p1logq1+p2logq2)=−(p1logq1+(1−p1)log(1−q1))
BCE 可用作二分類或多標簽分類的損失函數。
交叉熵損失前通常接Softmax,而二元交叉熵損失前通常接Sigmoid
二分類情景下,輸出層既可以采用一個神經元+Sigmoid也可以采用兩個神經元+Softmax,兩者等價,但使用前者訓練起來更快一些
BCE 還可通過 MLE 得到。給定 n n n 個樣本: x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,每個樣本的標簽 y i y_i yi 非 0 0 0 即 1 1 1( 1 1 1 代錶正類, 0 0 0 代錶負類),神經網絡的參數簡記為 θ \theta θ。我們的目標是尋找最優的 θ \theta θ 使得 y ^ i = P θ ( y i ∣ x i ) \hat{y}_i=\mathbb{P}_{\theta}(y_i|x_i) y^i=Pθ(yi∣xi)。設 x i x_i xi 被分類為正類的概率為 π i = P θ ( y i = 1 ∣ x i ) \pi_i=\mathbb{P}_{\theta}(y_i=1|x_i) πi=Pθ(yi=1∣xi),則對數似然函數為
ℓ ( θ ) = log L ( θ ) = log ∏ i = 1 n π i y i ( 1 − π i ) 1 − y i = ∑ i = 1 n y i log π i + ( 1 − y i ) log ( 1 − π i ) \begin{aligned} \ell(\theta)&=\log L(\theta) \\ &=\log \prod_{i=1}^n \pi_i^{y_i}(1-\pi_i)^{1-y_i} \\ &=\sum_{i=1}^ny_i\log \pi_i+(1-y_i)\log (1-\pi_i) \end{aligned} ℓ(θ)=logL(θ)=logi=1∏nπiyi(1−πi)1−yi=i=1∑nyilogπi+(1−yi)log(1−πi)
最大化 ℓ ( θ ) \ell(\theta) ℓ(θ) 等價於最小化 − ℓ ( θ ) -\ell(\theta) −ℓ(θ),而後者就是二元交叉熵損失。
博主才疏學淺,本文如有錯誤歡迎在評論區指出
边栏推荐
- Halcon color recognition_ fuses. hdev:classify fuses by color
- asp. Net (c)
- C#【必备技能篇】ConfigurationManager 类的使用(文件App.config的使用)
- Rebuild my 3D world [open source] [serialization-1]
- 12. Dynamic link library, DLL
- np. allclose
- Blue Bridge Cup provincial match simulation question 9 (MST)
- 一题多解,ASP.NET Core应用启动初始化的N种方案[上篇]
- Multiple linear regression (gradient descent method)
- Applet (use of NPM package)
猜你喜欢
![[beauty of algebra] singular value decomposition (SVD) and its application to linear least squares solution ax=b](/img/ee/8e07e2dd89bed63ff44400fe1864a9.jpg)
[beauty of algebra] singular value decomposition (SVD) and its application to linear least squares solution ax=b

Wechat H5 official account to get openid climbing account
Nodejs modularization
Applet (global data sharing)
深度学习模型与湿实验的结合,有望用于代谢通量分析
容易混淆的基本概念 成员变量 局部变量 全局变量
Ros-11 common visualization tools

我从技术到产品经理的几点体会

My university
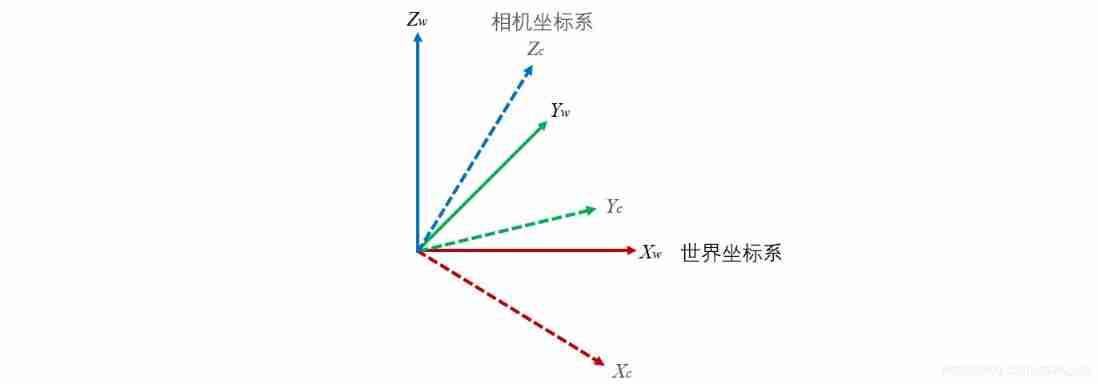
Understanding rotation matrix R from the perspective of base transformation
随机推荐
MPSoC QSPI flash upgrade method
Halcon snap, get the area and position of coins
Oracle advanced (III) detailed explanation of data dictionary
[code practice] [stereo matching series] Classic ad census: (5) scan line optimization
编辑器-vi、vim的使用
Count of C # LINQ source code analysis
[technical school] spatial accuracy of binocular stereo vision system: accurate quantitative analysis
Redis implements a high-performance full-text search engine -- redisearch
Nodejs modularization
Golang foundation -- map, array and slice store different types of data
kubeadm系列-00-overview
Pearson correlation coefficient
[code practice] [stereo matching series] Classic ad census: (4) cross domain cost aggregation
Programming implementation of ROS learning 6 -service node
C#图像差异对比:图像相减(指针法、高速)
Introduction Guide to stereo vision (1): coordinate system and camera parameters
ECMAScript6介绍及环境搭建
牛顿迭代法(解非线性方程)
Halcon blob analysis (ball.hdev)
[Niuke brush questions day4] jz55 depth of binary tree