当前位置:网站首页>数据分析系列 之3σ规则/依据拉依达准则来剔除异常值
数据分析系列 之3σ规则/依据拉依达准则来剔除异常值
2022-07-07 21:52:00 【琅晓琳】
1 相关原理
3σ原则为
数值分布在(μ-σ,μ+σ)中的概率为0.6827
数值分布在(μ-2σ,μ+2σ)中的概率为0.9545
数值分布在(μ-3σ,μ+3σ)中的概率为0.9973
可以认为,Y 的取值几乎全部集中在(μ-3σ,μ+3σ)区间内,超出这个范围的可能性仅占不到0.3%.
2 代码实现
public class Pauta{
//创建拉依达类
private double arr[]; //接受原始数组
public Pauta(double temp[]) {
//利用构造方法来得的原始数组
this.arr=temp;
System.out.print("原始数组:");
for(double x:arr) {
System.out.print(x+"、");
}
System.out.println();
}
public double average() {
//原始数组的算数平均值方法
double sum=0;
for(int x=0;x<arr.length;x++)
sum+=arr[x];
}
return sum/arr.length;
}
public double[] residualError() {
//原始数组的剩余误差方法
double rE[]=new double[] {
};
for(int x=0;x<arr.length;x++) {
rE[x]=arr[x]-average();
}
return rE;
}
public double standardVariance() {
//原始数组的标准方差值计算方法
double sum=0;
for(int int x=0;x<arr.length;x++) {
sum+=Math.pow(arr[x]-average(),2);
}
return Math.sqrt(sum/(arr.length-1));
}
public void judge() {
//判断异常值方法,若异常,则输出
for(int int x=0;x<arr.length;x++) {
if(Math.abs(arr[x]-average())>(3*standardVariance())) {
System.out.println("该数组中的第"+(x+1)+"个元素属于异常值");
}
}
}
}
public class client{
public static void main(String args[]) {
double data[]=new double[] {
1,2,8,10,8,5,2,4,6,11,15};//原始数组
Pauta pau=new Pauta(data);//原始数组封装后输出
System.out.println("算数平均值:"+pau.average());//算数平均值
/*此处的剩余误差输出略*/
System.out.println("标准方差:"+pau.standardVariance());//标准方差
pau.judge();//判断异常值方法
}
}
参考资料:
https://wenku.baidu.com/view/cce8bacc142ded630b1c59eef8c75fbfc77d9407.html JAVA使用:3σ规则、依据拉依达准则来剔除异常值程序
边栏推荐
猜你喜欢

B_QuRT_User_Guide(36)
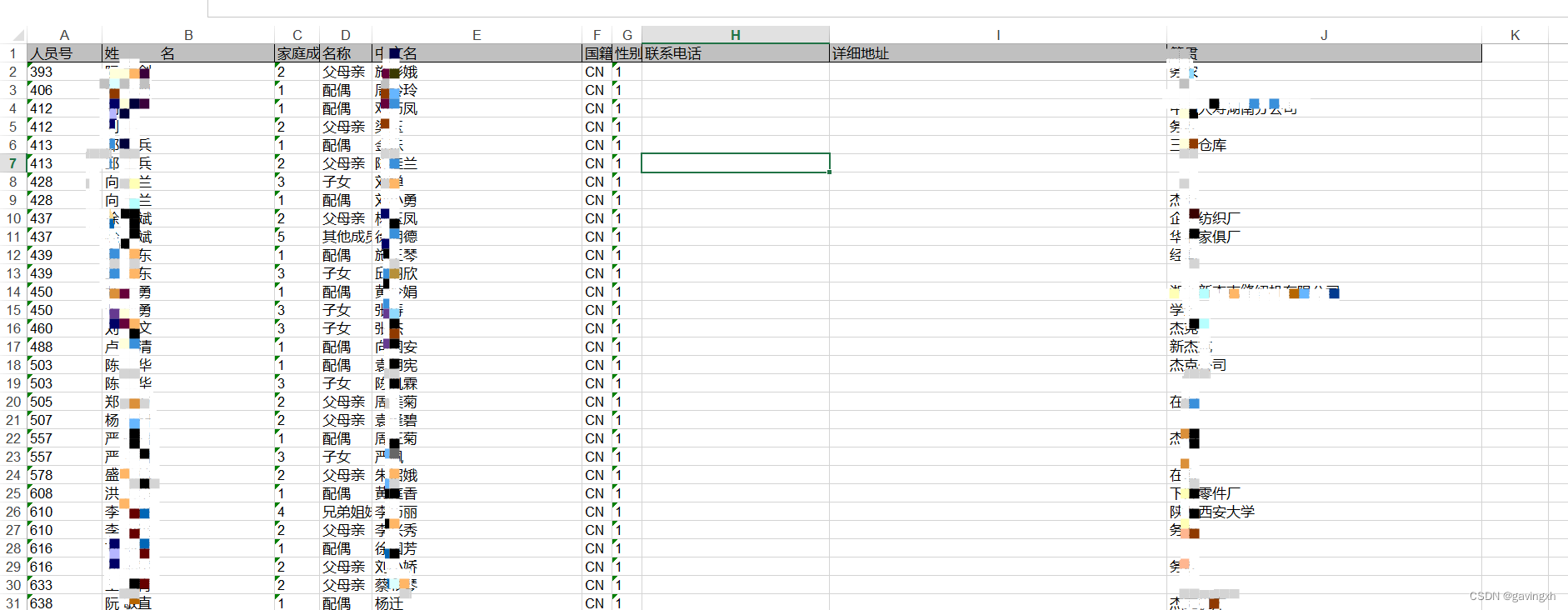
SAP HR family member information
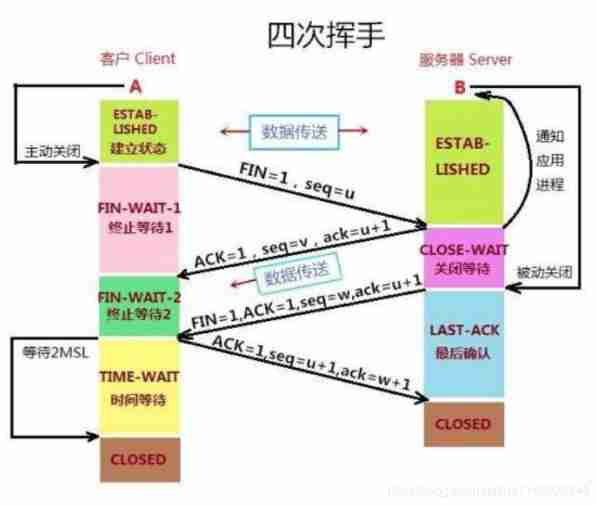
Understand TCP's three handshakes and four waves with love
![[compilation principle] lexical analysis design and Implementation](/img/8c/a3a50e6b029c49caf0d791f7d4513a.png)
[compilation principle] lexical analysis design and Implementation

S2b2b mall solution of intelligent supply chain in packaging industry: opening up a new ecosystem of e-commerce consumption
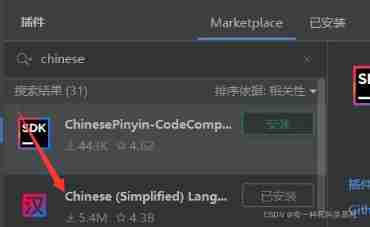
Pycharm essential plug-in, change the background (self use, continuous update) | CSDN creation punch in
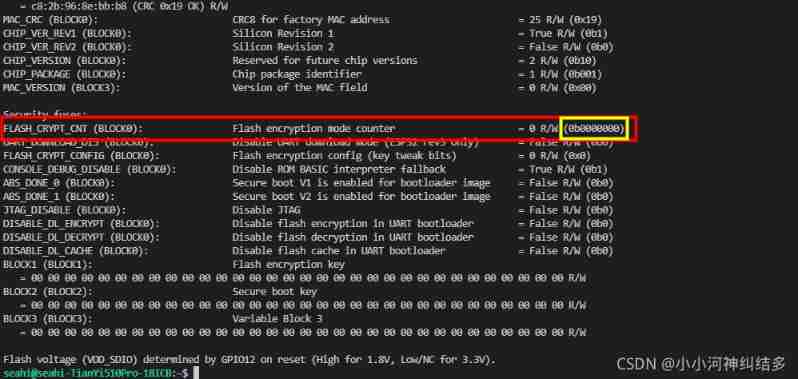
Flash encryption process and implementation of esp32
Live-Server使用

Idea automatically generates serialVersionUID

进度播报|广州地铁七号线全线29台盾构机全部完成始发
随机推荐
Illegal behavior analysis 1
平衡二叉树【AVL树】——插入、删除
生鲜行业数字化采购管理系统:助力生鲜企业解决采购难题,全程线上化采购执行
List. How to achieve ascending and descending sort() 2020.8.6
C method question 1
Oracle statistics by time
SAP HR奖罚信息导出
【7.4】25. K 个一组翻转链表
Summary of common methods of object class (September 14, 2020)
Design and implementation of spark offline development framework
C simple question 2
Matlab SEIR infectious disease model prediction
Possible SQL for Oracle table lookup information
Deep understanding of MySQL lock and transaction isolation level
B_ QuRT_ User_ Guide(37)
PCB wiring rules of PCI Express interface
One week learning summary of STL Standard Template Library
C method question 2
Given an array, such as [7864, 284, 347, 7732, 8498], now you need to splice the numbers in the array to return the "largest possible number."
Markdown