当前位置:网站首页>The 19th Zhejiang Provincial College Programming Contest 2022 f.easyfix chairman tree
The 19th Zhejiang Provincial College Programming Contest 2022 f.easyfix chairman tree
2022-07-07 23:21:00 【HeartFireY】
F.Easy Fix
Topic analysis
Given the permutation p 1 , p 2 , p 3 , … , p n p_1, p_2, p_3,\dots, p_n p1,p2,p3,…,pn, Definition A i A_i Ai It means that p i p_i pi Left side parallel p i p_i pi The number of small numbers , B i B_i Bi It means that p i p_i pi The right side is not bigger than p i p_i pi The number of small numbers , C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi). Now, given multiple operations ( l , r ) (l, r) (l,r), Ask for each operation , In exchange for ( p i , p j ) (p_i, p_j) (pi,pj) After ∑ C i \sum C_i ∑Ci.
First consider how to deal with the initial C i C_i Ci value , The following properties were observed :
- about A i A_i Ai The solution process of value is similar to the idea of finding reverse order pairs , You can maintain the tree array directly , O ( n log n ) O(n\log n) O(nlogn) Get all A i A_i Ai
- Because it's permutation , B i = p i − 1 − A i B_i = p_i - 1 - A_i Bi=pi−1−Ai Sure O ( 1 ) O(1) O(1) Get
- that C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi) It's also O ( 1 ) O(1) O(1) Got
Because each inquiry is independent , Then consider exchanging ( p l , p r ) (p_l, p_r) (pl,pr) Operation of C i C_i Ci Influence :
about [ 1 , l ) , ( r , n ] [1, l), (r , n] [1,l),(r,n] Number of ranges , C i C_i Ci Value must not affect . Because the switching operation is carried out on one side
about p l p_l pl, Exchange to r r r After the position , A l → A l + District between [ l , r ] Small On p l Of Count word individual Count A_l \rightarrow A_l + Section [l,r] Less than p_l The number of the number of Al→Al+ District between [l,r] Small On pl Of Count word individual Count , B l ’ B_l’ Bl’ You can still ask directly
about p r p_r pr, Exchange to l l l After the position , A r → A r − District between [ l , r ] Small On p r Of Count word individual Count A_r \rightarrow A_r - Section [l ,r] Less than p_r The number of the number of Ar→Ar− District between [l,r] Small On pr Of Count word individual Count , B r ’ B_r’ Br’ You can still ask directly
If we ask online ( Chairman tree maintenance ), So for p l , p r p_l,p_r pl,pr, In fact, it can be directly two O ( l o g n ) O(logn) O(logn) Ask again .
So the point is for [ l + 1 , r − 1 ] [l + 1, r - 1] [l+1,r−1] The number in the interval C i C_i Ci Value change , How to maintain ?
about p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr, If A i ≤ B i A_i \leq B_i Ai≤Bi, After exchange A i − 1 , B i + 1 A_i - 1, B_i + 1 Ai−1,Bi+1, thus C i − 1 C_i - 1 Ci−1
about p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr, If A i ≥ B i A_i \geq B_i Ai≥Bi, After exchange A i + 1 , B i − 1 A_i + 1, B_i - 1 Ai+1,Bi−1, thus C i − 1 C_i -1 Ci−1
about p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr, If A i − 1 ≥ B i + 1 , A i ≥ B i A_i - 1 \geq B_i + 1, A_i \geq B_i Ai−1≥Bi+1,Ai≥Bi, After exchange C i + 1 C_i + 1 Ci+1
about p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr, If A i − 1 ≤ B i + 1 , A i ≤ B i A_i - 1 \leq B_i + 1, A_i \leq B_i Ai−1≤Bi+1,Ai≤Bi, After exchange C i + 1 C_i + 1 Ci+1
So for the above four cases , We can use four chairman trees for maintenance . meanwhile , about p l , p r p_l, p_r pl,pr The contribution calculation of also needs to support the interval < K <K <K Number of numbers query , Therefore, a total of five chairman trees are required for maintenance , Complexity O ( m × 4 log n ) O(m \times 4 \log n) O(m×4logn).
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
const int N = 1e5 + 10;
int p[N], a[N], b[N], c[N], d[N];
using bset5 = std::bitset<5>;
namespace Fenwick{
int tree[N], len;
#define lowbit(x) ((x) & (-x))
inline void init(int ln){
len = ln; }
inline void update(int i, int x){
for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x; }
inline int getsum(int i, int ans = 0){
for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[pos]; return ans; }
}
namespace PresidentTree{
int root[N], sum[N << 5][5], lc[N << 5], rc[N << 5], cnt;
#define ls l, mid
#define rs mid + 1, r
void update(int &rt, int pre, int l, int r, int x, bset5 inc){
rt = ++cnt, lc[rt] = lc[pre], rc[rt] = rc[pre];
for(int i = 0; i <= 5; i++) sum[rt][i] = sum[pre][i] + (inc[i] ? 1 : 0);
if(l == r) return;
int mid = l + r >> 1;
if(x <= mid) update(lc[rt], lc[rt], l, mid, x, inc);
else update(rc[rt], rc[rt], mid + 1, r, x, inc);
}
int query(int st, int ed, int l, int r, int L, int R, int id){
if(l == L && r == R) return sum[ed][id] - sum[st][id];
int mid = l + r >> 1;
if(mid >= R) return query(lc[st], lc[ed], l, mid, L, R, id);
else if(mid >= L) return query(lc[st], lc[ed], l, mid, L, mid, id) + query(rc[st], rc[ed], mid + 1, r, mid + 1, R, id);
else return query(rc[st], rc[ed], mid + 1, r, L, R, id);
}
}
#define Pdt PresidentTree
inline void solve(){
int n = 0; std::cin >> n;
Fenwick::init(n);
for(int i = 1; i <= n; i++) std::cin >> p[i];
for(int i = 1; i <= n; i++){
a[i] = Fenwick::getsum(p[i]);
b[i]= p[i] - 1 - a[i];
Fenwick::update(p[i], 1);
c[i] = std::min(a[i], b[i]);
d[i] = d[i - 1] + c[i];
}
for(int i = 1; i <= n; i++){
bset5 flag; flag.reset();
if(a[i] <= b[i]) flag[1] = true;
if(a[i] >= b[i]) flag[3] = true;
if(a[i] - 1 >= b[i] + 1 && a[i] >= b[i]) flag[2] = true;
if(a[i] + 1 <= b[i] - 1 && a[i] <= b[i]) flag[4] = true;
flag[0] = true;
Pdt::update(Pdt::root[i], Pdt::root[i - 1], 1, n + 1, p[i], flag);
}
int m = 0; std::cin >> m;
while(m--){
int l, r; std::cin >> l >> r;
if(l == r){
std::cout << d[n] << endl; continue; }
else if(l > r) std::swap(l, r);
int ans = d[n] - c[l] - c[r];
if(p[l] < p[r]){
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 1)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 2);
} else {
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 3)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 4);
}
int nowa = Pdt::query(Pdt::root[0], Pdt::root[l - 1], 1, n + 1, 1, p[r], 0),
nowb = p[r] - 1 - nowa;
ans += std::min(nowa, nowb);
nowa = Pdt::query(Pdt::root[r], Pdt::root[n], 1, n + 1, 1, p[l], 0),
nowb = p[l] - 1 - nowa;
ans += std::min(nowa, nowb);
std::cout << ans << endl;
}
}
signed main(){
std::ios_base::sync_with_stdio(false), std::cin.tie(0);
solve();
return 0;
}
边栏推荐
- Puce à tension stabilisée LDO - schéma de bloc interne et paramètres de sélection du modèle
- Matlab-SEIR传染病模型预测
- Adrnoid开发系列(二十五):使用AlertDialog创建各种类型的对话框
- 力扣解法汇总648-单词替换
- Archlinux install MySQL
- RE1 attack and defense world reverse
- 聊聊支付流程的设计与实现逻辑
- JMeter interface automated test read case, execute and write back result
- Technology at home and abroad people "see" the future of audio and video technology
- Two kinds of curves in embedded audio development
猜你喜欢
微信论坛交流小程序系统毕业设计毕设(5)任务书

微信论坛交流小程序系统毕业设计毕设(2)小程序功能
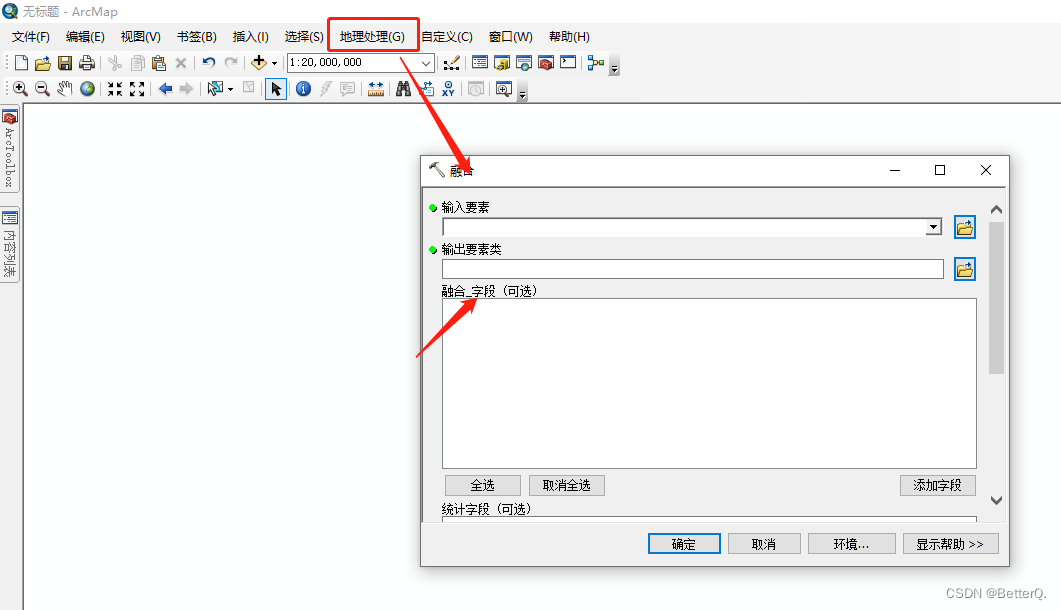
ArcGIS:矢量要素相同字段属性融合的两种方法

RE1 attack and defense world reverse

Inftnews | the wide application of NFT technology and its existing problems

re1攻防世界逆向
![[microservices SCG] gateway integration Sentinel](/img/f3/410d7228b4b253ebf41015a785099f.png)
[microservices SCG] gateway integration Sentinel
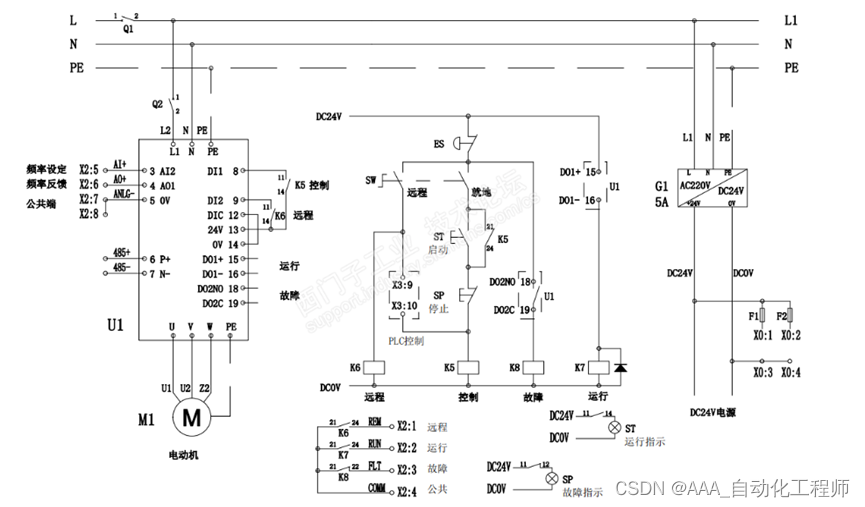
Specific method example of V20 frequency converter manual automatic switching (local remote switching)
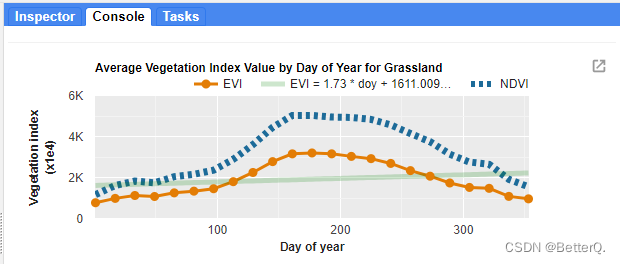
Gee (IV): calculate the correlation between two variables (images) and draw a scatter diagram

PMP项目管理考试过关口诀-1
随机推荐
Installing vmtools is gray
Network security sqlmap and DVWA explosion
Dynamics 365 find field filtering
kubernetes的简单化数据存储StorageClass(建立和删除以及初步使用)
Bea-3xxxxx error code
FPGA基础篇目录
LeeCode -- 6. Z 字形变换
leetcode-520. Detect capital letters -js
网络安全-beef
The text editor of markdown class should add colors to fonts (including typora, CSDN, etc.)
13、 System optimization
LDO稳压芯片-内部框图及选型参数
Inftnews | the wide application of NFT technology and its existing problems
Specific method example of V20 frequency converter manual automatic switching (local remote switching)
七月第一周
网络安全-对操作系统进行信息查询
USB(十五)2022-04-14
微信论坛交流小程序系统毕业设计毕设(3)后台功能
What are the similarities and differences between smart communities and smart cities
云原生数据仓库AnalyticDB MySQL版用户手册