当前位置:网站首页>2021ICPC上海 H.Life is a Game Kruskal重构树
2021ICPC上海 H.Life is a Game Kruskal重构树
2022-07-07 21:50:00 【HeartFireY】
H.Life is a Game Kruskal重构树
题目分析
给定一张 n n n个点 m m m条边的无向图,以及 q q q个询问。对于每个询问,给定初始点和初始经验值,经过一条边要求当前经验值大于边权,经过一个点后点权累加至经验值。求能够获得的最大经验。
首先容易证明,对于最终的答案,两个点之间的所有简单路径上最大边权的最小值 = 最小生成树上两个点之间的简单路径上的最大值 = K r u s k a Kruska Kruskal 重构树上两点之间的 L C A LCA LCA 的权值
那么容易想到对原图建 K r u s k a l Kruskal Kruskal重构树,不妨先对样例建树:
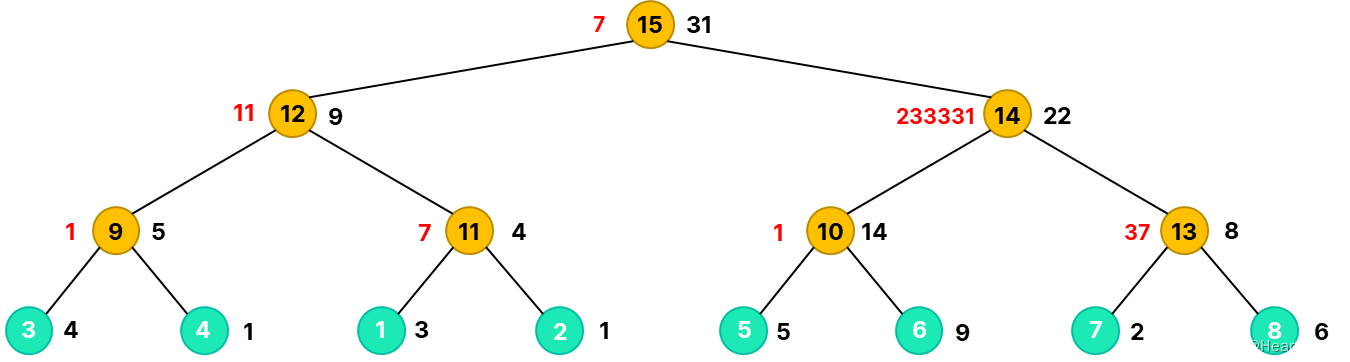
红色数字表示 K r u s k a l Kruskal Kruskal重构树的点权,即为原图最大边权最小值。叶节点均为原图节点,黑色数字表示经验值,由于后期计算方便需要,将经验值自叶子节点向根节点求和。
那么我们对于某个询问,只需要从对应的叶节点开始往上跳到祖先节点,直至跳不过去(经验值小于点权(红色数字)),同时我们处理出了到达每个父节点能够获得的经验值(黑色数字),这样只需要一路往上跳检查是否满足经验值大于 K r u s k a l Kruskal Kruskal重构树的点权值就可以了。
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10;
int n, m, q;
int pnt[N], val[N];
struct unionfind{
int par[N];
unionfind(int n){
for(int i = 1; i <= n; i++) par[i] = i; }
int find(int x){
return x == par[x] ? x : (par[x] = find(par[x])); }
void merge(int u, int v){
int fau = find(u), fav = find(v);
if(fau != fav) par[fav] = fau;
}
int ismerge(int u, int v){
return find(u) == find(v); }
};
vector<int> g[N];
namespace KR{
struct edge{
int u, v ,w;
const bool operator< (const edge &x) const {
return w < x.w; }
}edges[N];
inline void add_edge(int i, int u, int v, int w){
edges[i] = {
u ,v, w}; }
int kruskal(){
int tot = n, cnt = 0;
unionfind uf(n + 20);
sort(edges + 1, edges + 1 + m);
for(int i = 1; i <= m; i++){
int nu = edges[i].u, nv = edges[i].v, nw = edges[i].w;
int fau = uf.find(nu), fav = uf.find(nv);
if(fau != fav){
val[++tot] = edges[i].w;
uf.par[tot] = uf.par[fau] = uf.par[fav] = tot;
g[fau].emplace_back(tot), g[fav].emplace_back(tot);
g[tot].emplace_back(fau), g[tot].emplace_back(fav);
cnt++;
}
if(cnt == n - 1) break;
}
return tot;
}
}
int fa[N][20];
void dfs0(int u, int ufa){
fa[u][0] = ufa;
for(int i = 1; i < 20; i++) fa[u][i] = fa[fa[u][i - 1]][i - 1];
for(auto v : g[u]){
if(v == ufa) continue;
dfs0(v, u);
pnt[u] += pnt[v];
}
}
using KR::add_edge;
using KR::kruskal;
inline void solve(){
cin >> n >> m >> q;
for(int i = 1; i <= n; i++) cin >> pnt[i];
for(int i = 1; i <= m; i++){
int u, v, w; cin >> u >> v >> w;
add_edge(i, u, v ,w);
}
n = kruskal();
dfs0(n, 0);
val[0] = 1e18;
while(q--){
int u, s; cin >> u >> s;
int ans = pnt[u] + s;
while(u != n){
int t = u;
for(int i = 19; i >= 0; i--)
if(val[fa[u][i]] <= ans) u = fa[u][i];
if(t == u) break;
ans = pnt[u] + s;
}
cout << ans << endl;
}
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
边栏推荐
- Introduction to anomaly detection
- Talk about DART's null safety feature
- Knowledge drop - PCB manufacturing process flow
- Online interview, how to better express yourself? In this way, the passing rate will be increased by 50%~
- Wechat forum exchange applet system graduation design (5) assignment
- 微信论坛交流小程序系统毕业设计毕设(6)开题答辩PPT
- 海内外技术人们“看”音视频技术的未来
- Unity dynamically merges mesh textures
- QT graphicsview graphical view usage summary with flow chart development case prototype
- The wonderful relationship between message queue and express cabinet
猜你喜欢
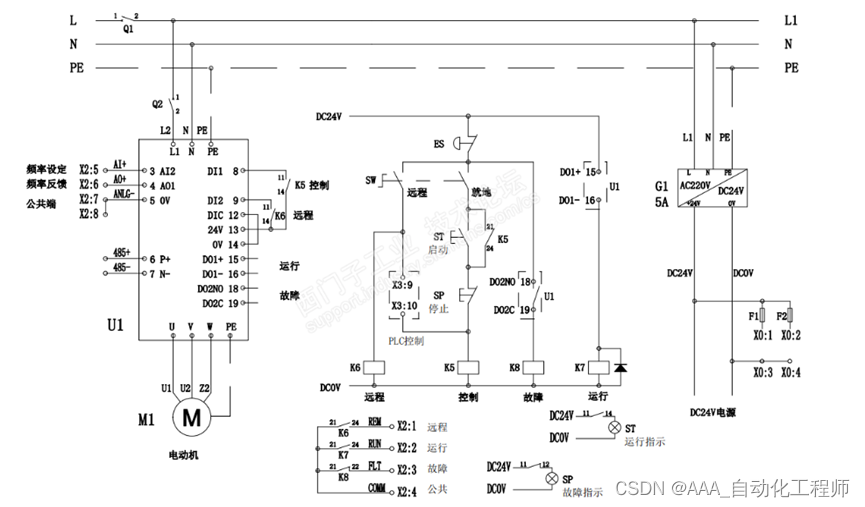
Specific method example of V20 frequency converter manual automatic switching (local remote switching)
Software test classification

JMeter interface automated test read case, execute and write back result
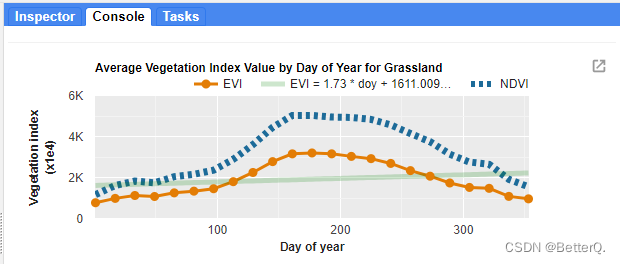
Gee (IV): calculate the correlation between two variables (images) and draw a scatter diagram
14、 Two methods of database export and import

Wechat forum exchange applet system graduation design completion (7) Interim inspection report
微信论坛交流小程序系统毕业设计毕设(5)任务书

Lecture 30 linear algebra Lecture 5 eigenvalues and eigenvectors
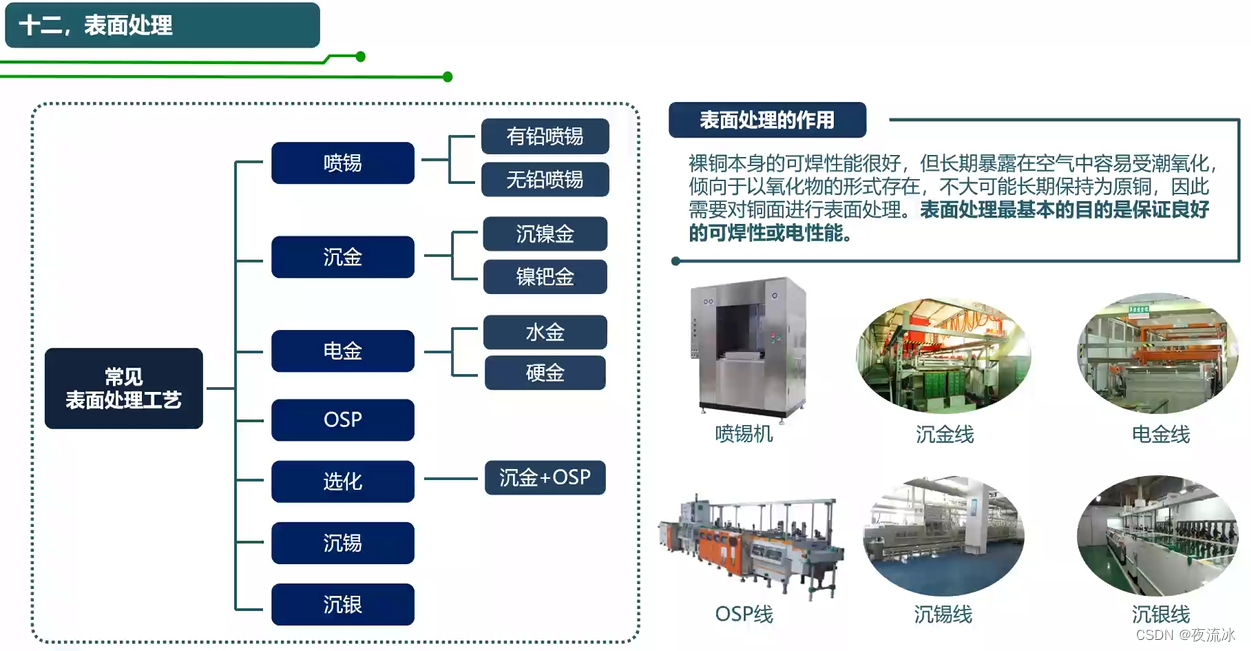
Knowledge drop - PCB manufacturing process flow
【刷题记录】3. 无重复字符的最长子串
随机推荐
Network security -beef
2021-01-12
There is another problem just online... Warm
JMeter interface automated test read case, execute and write back result
Gee (IV): calculate the correlation between two variables (images) and draw a scatter diagram
微信论坛交流小程序系统毕业设计毕设(5)任务书
Adults have only one main job, but they have to pay a price. I was persuaded to step back by personnel, and I cried all night
USB(十四)2022-04-12
The wonderful relationship between message queue and express cabinet
今日创见|企业促进创新的5大关键要素
Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to jsp-2
Install a new version of idea. Double click it to open it
GEE(四):计算两个变量(影像)之间的相关性并绘制散点图
定位到最底部[通俗易懂]
开发那些事儿:Go加C.free释放内存,编译报错是什么原因?
FPGA基础篇目录
Clean C disk
Network security - information query of operating system
OC variable parameter transfer
Inftnews | web5 vs Web3: the future is a process, not a destination