当前位置:网站首页>曼哈顿距离与曼哈顿矩形-打印回字型矩阵
曼哈顿距离与曼哈顿矩形-打印回字型矩阵
2022-07-06 06:01:00 【starnight531】
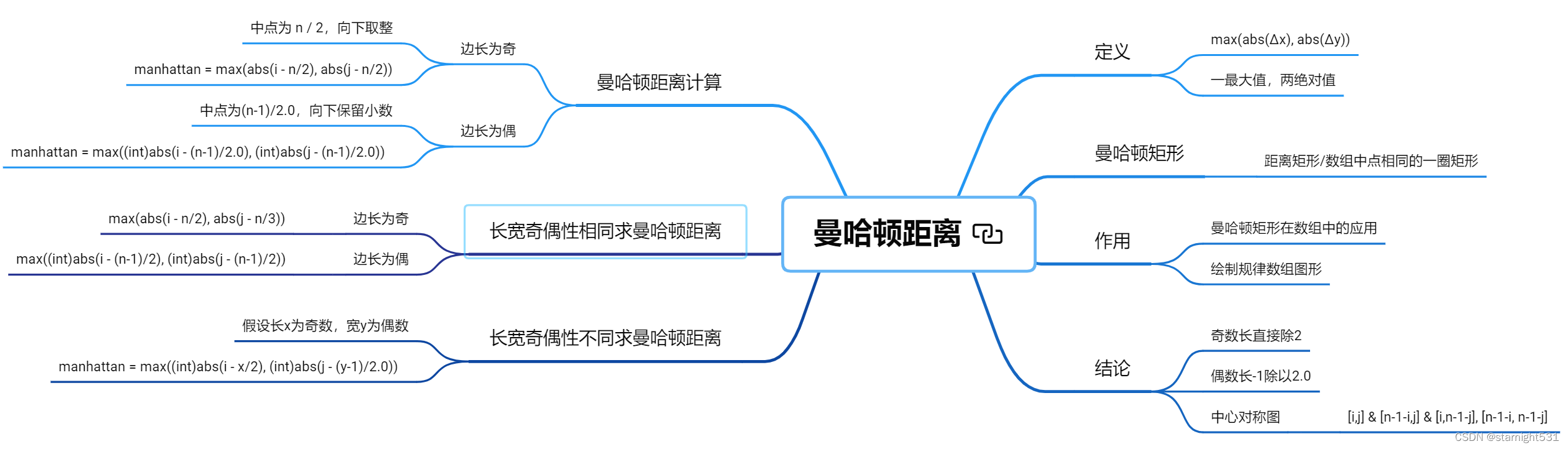
曼哈顿距离与曼哈顿矩形
食用指南:
Leetcode专栏开启了,由于博主闭关期末,所以每日只能一题尽量做到一题多解,先说思路,之后代码实现,会添加必要注释语法或STL内容会在注意点中点出,新手友好欢迎关注博主神机百炼专栏,内涵算法基础详细讲解和代码模板
题目描述:
输入整数 N,输出一个 N 阶的回字形二维数组。
数组的最外层为 1,次外层为 2,以此类推。
输入格式
输入包含多行,每行包含一个整数 N。
当输入行为 N=0 时,表示输入结束,且该行无需作任何处理。输出格式
对于每个输入整数 N,输出一个满足要求的 N 阶二维数组。
每个数组占 N 行,每行包含 N 个用空格隔开的整数。
每个数组输出完毕后,输出一个空行。数据范围
0≤N≤100
输入样例:
1
2
3
4
5
0
输出样例:
11 1
1 11 1 1
1 2 1
1 1 11 1 1 1
1 2 2 1
1 2 2 1
1 1 1 11 1 1 1 1
1 2 2 2 1
1 2 3 2 1
1 2 2 2 1
1 1 1 1 1题目来源:https://www.acwing.com/problem/content/755/
题目分析:
法一:曼哈顿距离
曼哈顿距离是两点在垂直坐标系中,x & y方向投影距离最大值
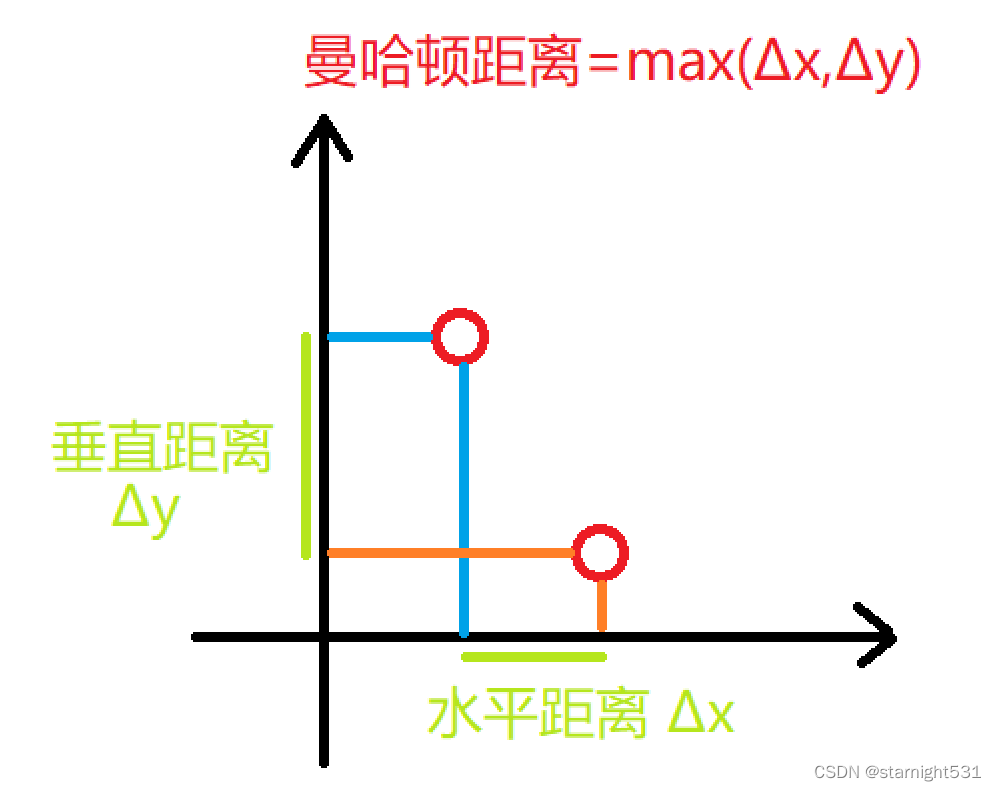
应用在数组/矩阵中,曼哈顿距离相同的点集合成为围绕矩阵中心的一圈矩形,
在计算曼哈顿距离时,需要区分行数/列数的奇偶:
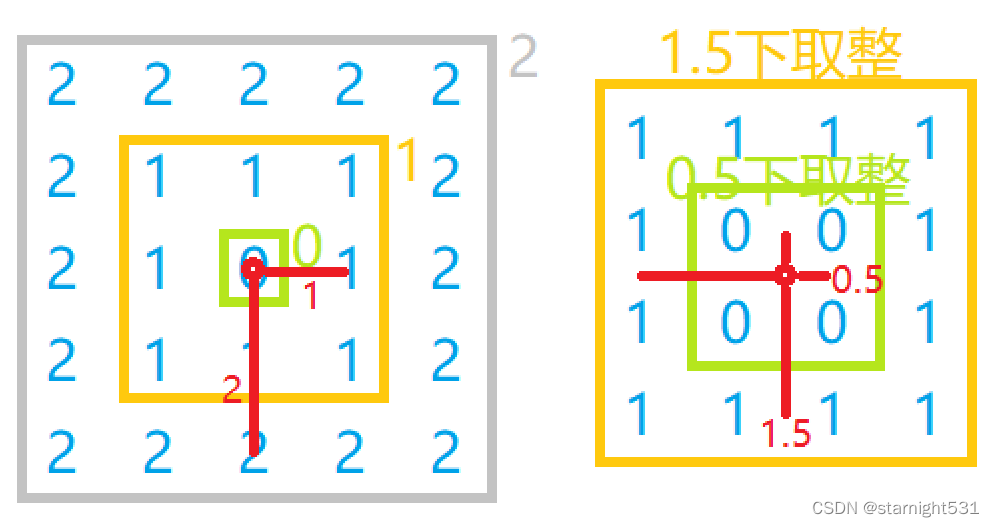
法二:数组下标与值的关系
曼哈顿距离其实就是数组下标和值关系研究所得的结论
当你不知道曼哈顿距离时,不妨试试手动探究一下,可能得到非曼哈顿距离的其他结论
方向1:用距离推导关系
- 该图关于中心对称
未越过中线的点用i计算,越过中线的点用n-1-i计算,
则对于所有点,要么 i 和 n-1-i/n-i 各计算一次,两者取最大/小值, 要么采用绝对值
2. 对于未过中线的点,采用举例探究
n = 5时,n/2 = 2,中点为(2, 2)
第一个点arr[0][0] = 1,距离中点Δx = Δy =2
第二个点arr[1][0] = 1,距离终点Δx = 2, Δy =1
第三个点arr[0][1] = 1,距离终点Δx = 1, Δy =2
确定计算公式:n/2 - max(abs(x-n/2) , abs(y-n/2)) + 1
3. 对于过了中线的点,采用举例探究
n = 5时,n/2 = 2,中点为(2, 2)
第一个点arr[4][4] = 1,距离中点Δx = Δy =2
第二个点arr[3][4] = 1,距离终点Δx = 1, Δy =2
第三个点arr[4][3] = 1,距离终点Δx = 2, Δy =1
确定计算公式:n/2 - max(abs(x-n/2) , abs(y-n/2)) + 1
- 完成用距离推导后,你会发现你其实推得的就是曼哈顿距离,
方向2:只看下标和值关系
- n = 5时:
- 对于未过中线的点,采用举例探究:
第一个点arr[0][0] = 1,1 = max/min(x + 1, y + 1)
第二个点arr[1][0] = 1,1 = min(x + 1, y + 1)
第三个点arr[0][1] = 1,1 = min(x + 1, y + 1)
石锤采用min(x + 1, y + 1) - 对于过了中线的点,采用举例探究:
第一个点arr[4][4] = 1,1 = max/min(n-x, n-y)
第二个点arr[3][4] = 1,1 = min(n-x, n-y)
第三个点arr[4][3] = 1,1 = min(n-x, n-y)
石锤采用min(n-x, n-y)
3.整体来看所有点:
现在有两种方案:min(x + 1, y + 1) & min(n-x, n-y)
查看是否同时采用/舍弃哪一种?
对于点arr[3][4],min(x + 1, y + 1) = 4, min(n-x, n-y) = 1
对于点arr[0][0],min(x + 1, y + 1) = 1, min(n-x, n-y) = 5
发现对于每个点都取两种方案的最小值,所以得出结论:
- 对于未过中线的点,采用举例探究:
- 所以对于所有点:arr[i][j] = min(min(x + 1, y + 1) , min(n-x, n-y));
法三:对称化简(严格说属于技巧而非方法)
中心对称图像,填写一点相当于填写了4点。
以n = 5的矩形为例,查看对称的4点下标关系:

在填写一个象限的值时,可以采用曼哈顿矩阵法 / 下标与值关系规律
这个技巧提升了时间复杂度,将时间缩减到原本的四分之一
也可以在之后题目中作为一个化简找规律时的思考出发点
算法模板:
- 曼哈顿距离 + 中心对称规律 本身就是基础算法,无模板
代码实现:
法一:
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(true){
int n = sc.nextInt();
if (n == 0) return; //读取终止出口
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(n % 2 == 1)
//曼哈顿距离近者,值大,距离为0者值为(n+1)/2
System.out.print((n+1)/2 - Math.max(Math.abs(n/2-i), Math.abs(n/2-j)) +" ");
else
//曼哈顿距离近者,值大,距离为0者值为n/2
System.out.print((n/2) - Math.max((int)Math.abs((n-1)/2.0-i), (int)Math.abs((n-1)/2.0-j)) +" ");
}
System.out.println();
}
System.out.println();
}
}
}
法二:
- 下标和值关系:Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j))
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(true){
int n = sc.nextInt();
if (n == 0) return; //读取终止出口
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
System.out.print(Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j))+" ");
}
System.out.println();
}
System.out.println();
}
}
}
法三:
- 曼哈顿距离填法:
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(true){
int n = sc.nextInt();
if (n == 0) return; //读取终止出口
int[][] arr = new int[n][n];
//偶数行列,如4行4列,只需填0~1行 & 0~1列
if(n % 2 == 0){
for(int i=0; i<n/2; i++){
for(int j=0; j<n/2; j++){
arr[i][j] = arr[n-1-i][n-1-j]
= arr[n-1-i][j] = arr[i][n-1-j]
= n/2 - Math.max(Math.abs((int)((n-1)/2.0 - i)), Math.abs((int)((n-1)/2.0 - j)));
}
}
}
//奇数行列,如5行5列,需要填0~2行 & 0~2列
else{
for(int i=0; i<=n/2; i++){
for(int j=0; j<=n/2; j++){
arr[i][j] = arr[n-1-i][n-1-j]
= arr[n-1-i][j] = arr[i][n-1-j]
= (n+1)/2 - Math.max(Math.abs(n/2 - i), Math.abs(n/2 - j));
}
}
}
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
System.out.print(arr[i][j]+" ");
}
System.out.println();
}
System.out.println();
}
}
}
- 下标和值关系填法:
import java.util.Scanner;
import java.lang.Math;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(true){
int n = sc.nextInt();
if (n == 0) return; //读取终止出口
int[][] arr = new int[n][n];
//偶数行列,如4行4列,只需填0~1行 & 0~1列
if(n % 2 == 0){
for(int i=0; i<n/2; i++){
for(int j=0; j<n/2; j++){
arr[i][j] = arr[n-1-i][n-1-j] = arr[n-1-i][j] = arr[i][n-1-j] = Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j));
}
}
}
//奇数行列,如5行5列,需要填0~2行 & 0~2列
else{
for(int i=0; i<=n/2; i++){
for(int j=0; j<=n/2; j++){
arr[i][j] = arr[n-1-i][n-1-j] = arr[n-1-i][j] = arr[i][n-1-j] = Math.min(Math.min(i+1, j+1), Math.min(n-i, n-j));
}
}
}
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
System.out.print(arr[i][j]+" ");
}
System.out.println();
}
System.out.println();
}
}
}
注意点:
曼哈顿距离计算公式:
- 行/列数为奇:
manhattan = max(abs(x - n/2), abs(y - n/2));
即中点 n/2 向下取整,而结果本身是整数 - 行/列数为偶:
manhattan = max((int)abs(x - (n-1)/2.0), (int)abs(y-(n-1)/2.0));
即中点为小数不取整,而 x - (n-1)/2.0的结果向下取整 - 可以简记为,奇数中点直接除2,偶数中点-1除以2.0
- 行/列数为奇:
对于安全性要求较高的Java
double 和 int 运算,也是先Int整型提升到double再与double运算
将Double用(int)显式类型转化为int,也是默认向下取整
边栏推荐
- A complete collection of necessary learning websites for office programmers
- Testing and debugging of multithreaded applications
- MPLS test report
- 【eolink】PC客户端安装
- Introduction to promql of # yyds dry goods inventory # Prometheus
- P问题、NP问题、NPC问题、NP-hard问题详解
- [happy Spring Festival] if you feel happy, dance
- Summary of data sets in intrusion detection field
- Application du Groupe Li dans gtsam
- [C language syntax] the difference between typedef struct and struct
猜你喜欢

Yunxiaoduo software internal test distribution test platform description document

LAN communication process in the same network segment
Memory and stack related concepts

Request forwarding and redirection

数学三大核心领域概述:代数
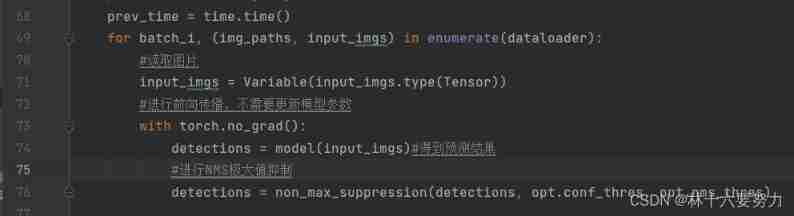
(5) Explanation of yolo-v3 core source code (3)
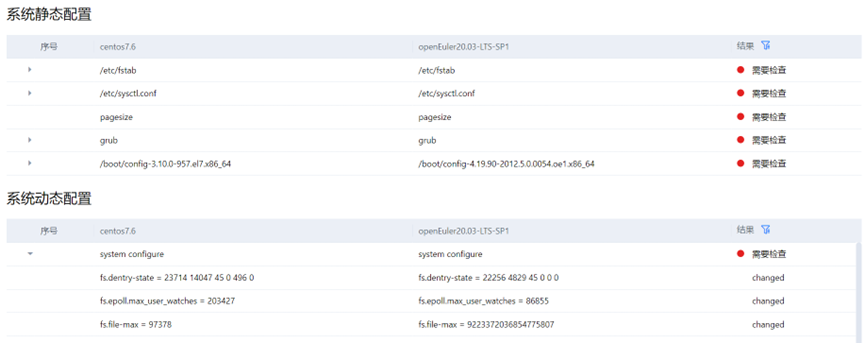
Practice sharing: how to safely and quickly migrate from CentOS to openeuler

华为路由器如何配置静态路由
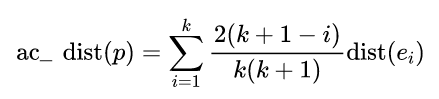
异常检测方法总结
![[course notes] Compilation Principle](/img/cc/34e86087cc5698f9bed91675369265.jpg)
[course notes] Compilation Principle
随机推荐
The usage and difference between strlen and sizeof
如何在业务代码中使用 ThinkPHP5.1 封装的容器内反射方法
Request forwarding and redirection
Usage of test macro of GTEST
Pay attention to the details of pytoch code, and it is easy to make mistakes
Auto. JS learning notes 17: basic listening events and UI simple click event operations
【Postman】Collections配置运行过程
Practice sharing: how to safely and quickly migrate from CentOS to openeuler
Gtest之TEST宏的用法
Testing and debugging of multithreaded applications
Cognitive introspection
Novice entry SCM must understand those things
Grant Yu, build a web page you want from 0
LAN communication process in the same network segment
Clock in during winter vacation
HCIA复习
《卓有成效的管理者》读书笔记
Function of activation function
Raised a kitten
数学三大核心领域概述:几何