当前位置:网站首页>【luogu P3295】萌萌哒(并查集)(倍增)
【luogu P3295】萌萌哒(并查集)(倍增)
2022-07-05 23:34:00 【SSL_TJH】
萌萌哒
题目链接:luogu P3295
题目大意
给你一个大的数,然后有一些限制条件是如果把这个数看做一个串,有几对长度分别相同的子串是相同的。
然后问你有多少个数满足条件。
思路
可以发现基本跟数字没关系,就唯一的就是第一位不能是 0 0 0。
然后你会发现关系都是两个位置是同一个数,然后你考虑统计最后有多少数之间互不相关,如果是 n u m num num,那答案就是 9 ∗ 1 0 n u m − 1 9*10^{num-1} 9∗10num−1。
然后暴力一个一个合并是 n 2 n^2 n2 的,但是询问只是 n n n,我们考虑能不能中和一下。
先考虑怎么把操作变成 log n \log n logn,不难想到可以把它拆成 log n \log n logn 个区间,可以有倍增拆或者放到线段树上。
但是因为你是要一一对应的,你线段树上看起来就不太行了。
那我们考虑用倍增的方法拆,然后看看询问。
我们发现倍增的块内部我们弄并查集,它每个点是可以拆开乘两个的,但是也不能跟所有并查集里面的点拆开来的都连啊。
发现那样搞很冗余,我们考虑高效一点,观察到你并查集其实是用树的形式连接起来的,我们直接就跟父亲连边即可。
(就两边拆开两边分别连边)
然后就可以啦。
代码
#include<cstdio>
#define ll long long
#define mo 1000000007
using namespace std;
const int N = 1e5 + 100;
int n, m, fa[21][N];
ll ksm(ll x, ll y) {
ll re = 1; while (y) {
if (y & 1) re = re * x % mo; x = x * x % mo; y >>= 1;} return re;
}
int find(int now) {
return fa[(now - 1) / n][now - (now - 1) / n * n] == now ? now : fa[(now - 1) / n][now - (now - 1) / n * n] = find(fa[(now - 1) / n][now - (now - 1) / n * n]);}
void merge(int x, int y) {
int X = find(x), Y = find(y); if (X != Y) fa[(X - 1) / n][X - (X - 1) / n * n] = Y;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i <= 20; i++) for (int j = 1; j + (1 << i) - 1 <= n; j++)
fa[i][j] = i * n + j;
for (int i = 1; i <= m; i++) {
int l1, r1, l2, r2; scanf("%d %d %d %d", &l1, &r1, &l2, &r2);
for (int j = 20; j >= 0; j--)
if (l1 + (1 << j) - 1 <= r1) {
merge(j * n + l1, j * n + l2);
l1 = l1 + (1 << j); l2 = l2 + (1 << j);
}
}
for (int i = 20; i > 0; i--)
for (int j = 1; j + (1 << i) - 1 <= n; j++) {
if (fa[i][j] != i * n + j) {
int fi = (fa[i][j] - 1) / n, fj = fa[i][j] - fi * n;
merge((i - 1) * n + j, (fi - 1) * n + fj);
merge((i - 1) * n + j + (1 << (i - 1)), (fi - 1) * n + fj + (1 << (fi - 1)));
}
}
int num = 0;
for (int i = 1; i <= n; i++) {
if (fa[0][i] == i) num++;
}
printf("%lld", 9ll * ksm(10, num - 1) % mo);
return 0;
}
边栏推荐
- CIS benchmark tool Kube bench
- How to insert data into MySQL database- How can I insert data into a MySQL database?
- idea 连接mysql ,直接贴配置文件的url 比较方便
- Switching power supply buck circuit CCM and DCM working mode
- 进击的技术er——自动化
- Technical specifications and model selection guidelines for TVs tubes and ESD tubes - recommended by jialichuang
- Rasa 3.x 学习系列-Rasa 3.2.1 新版本发布
- 4点告诉你实时聊天与聊天机器人组合的优势
- Qcombox (rewrite) + qcompleter (auto completion, auto loading the drop-down options of qcombox, setting the background color)
- When to use useImperativeHandle, useLayoutEffect, and useDebugValue
猜你喜欢

Bao Yan notebook IV software engineering and calculation volume II (Chapter 8-12)
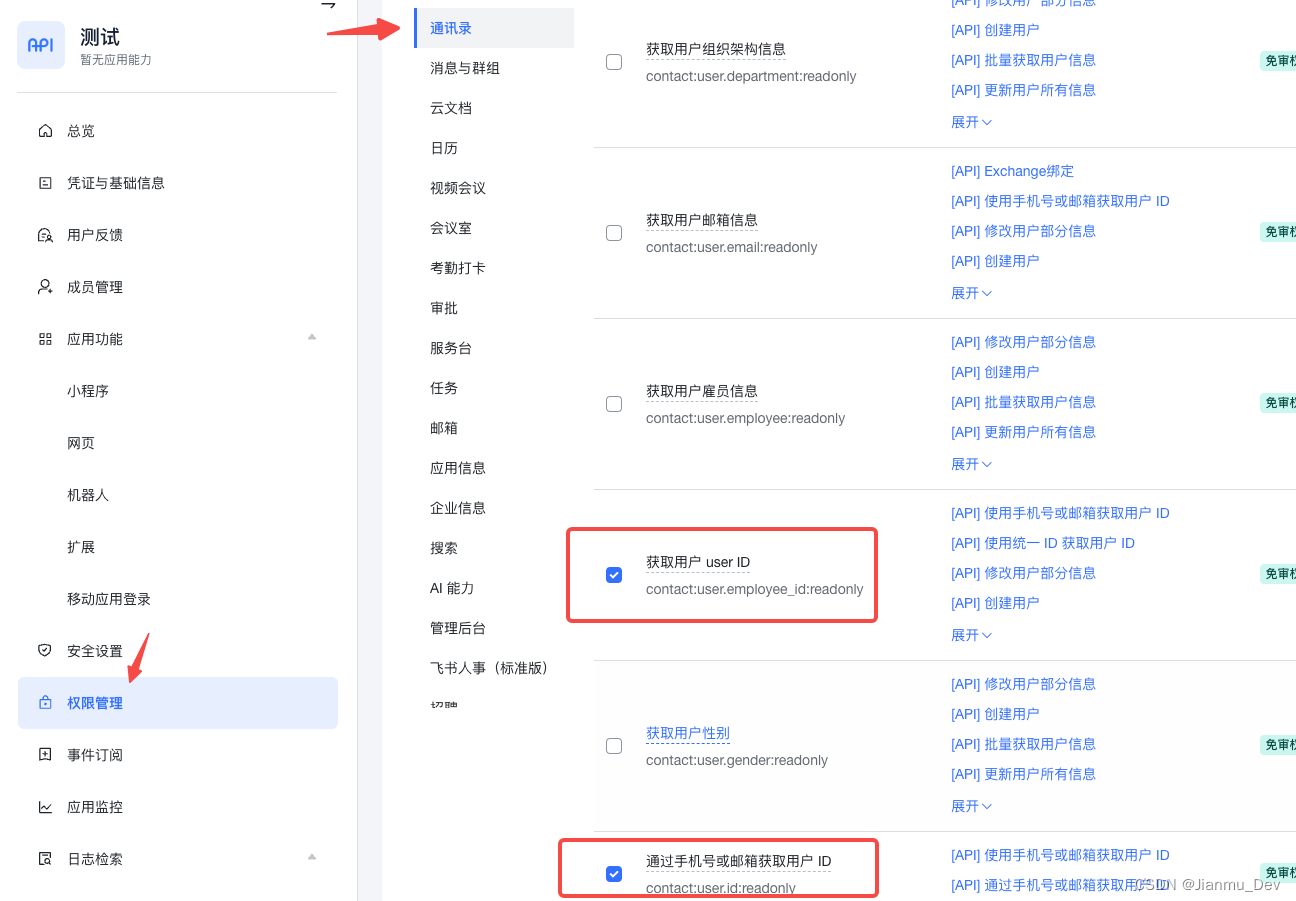
My colleagues quietly told me that flying Book notification can still play like this
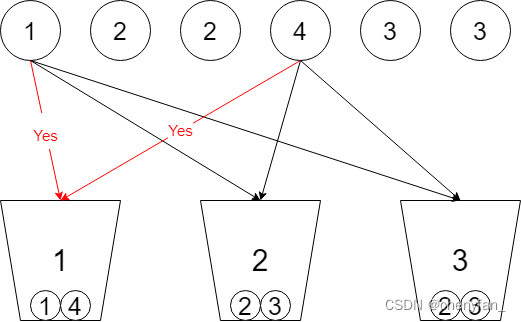
698. 划分为k个相等的子集 ●●
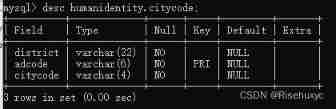
MySQL replace primary key delete primary key add primary key
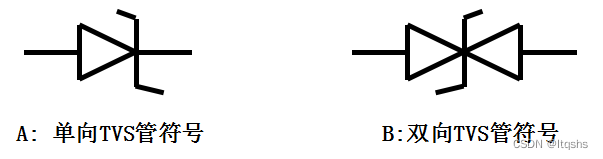
Comparison of parameters between TVs tube and zener diode
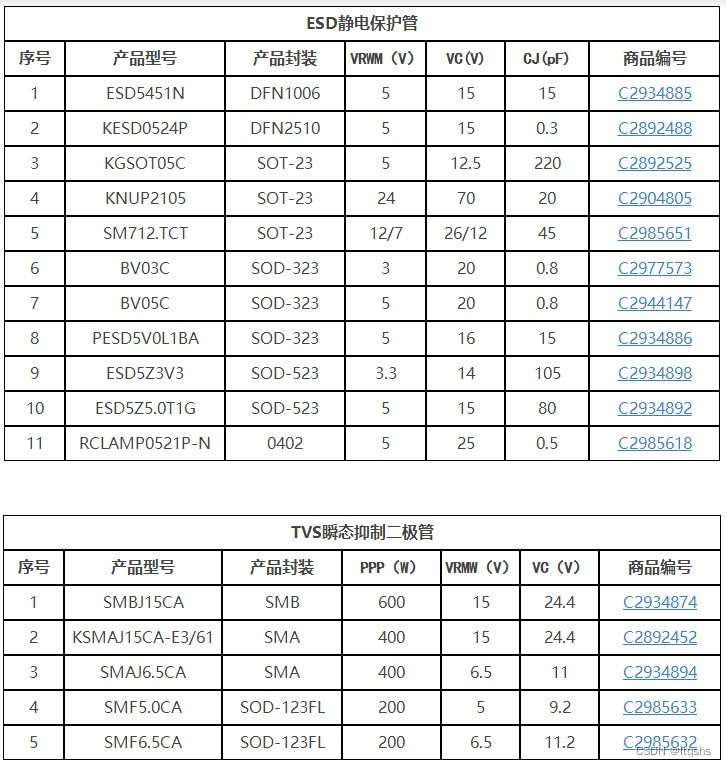
Spécifications techniques et lignes directrices pour la sélection des tubes TVS et ESD - Recommandation de jialichuang
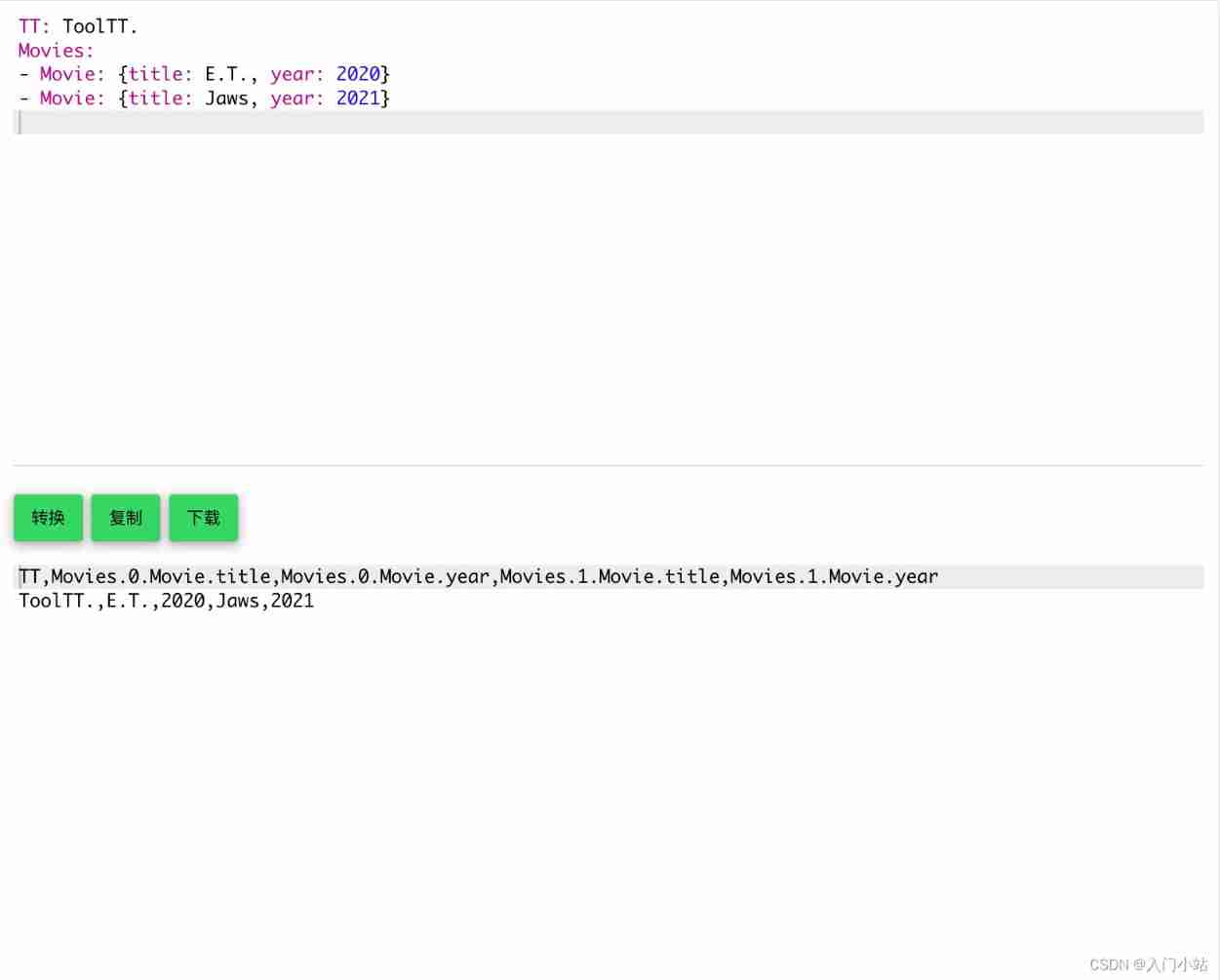
Online yaml to CSV tool
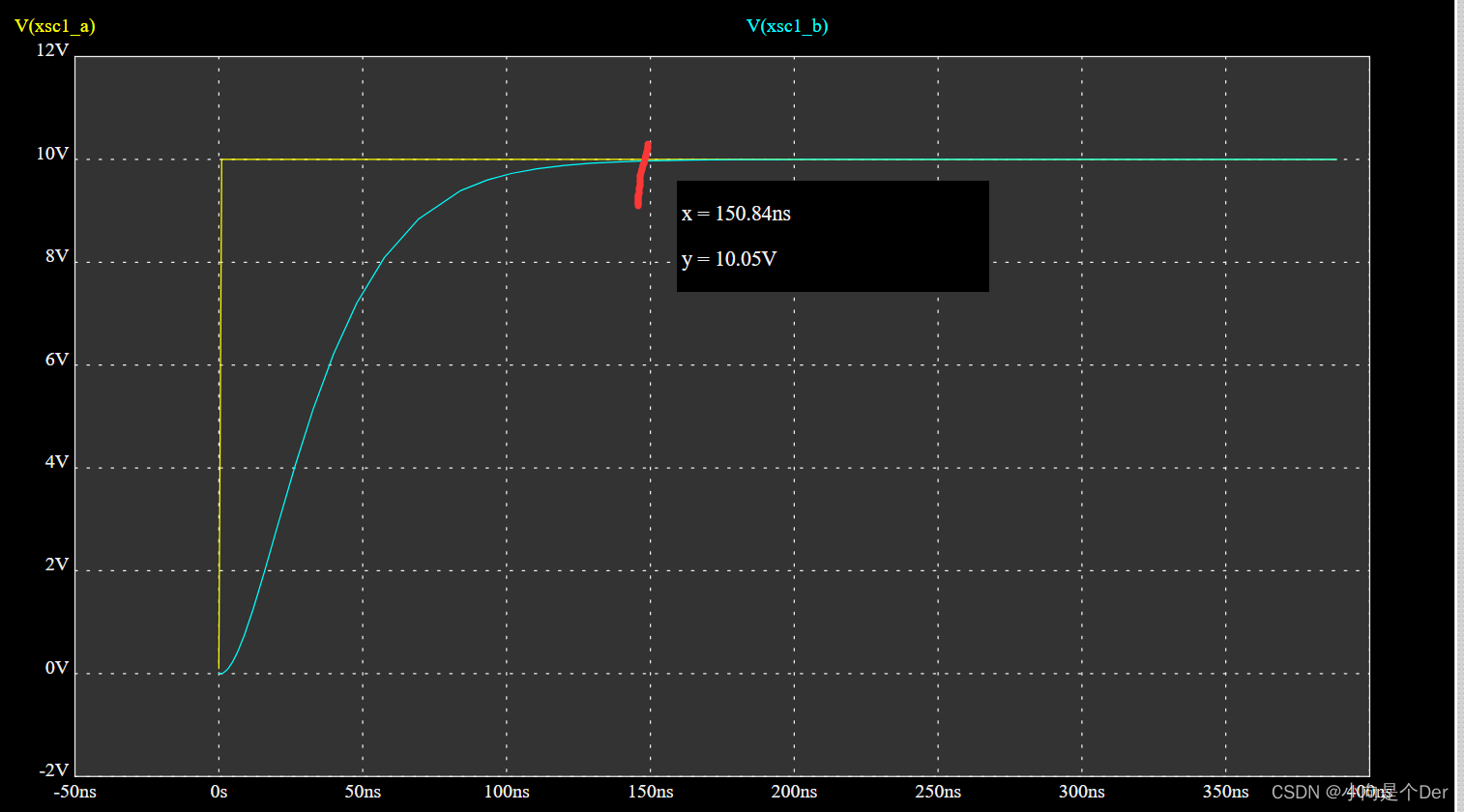
Brushless drive design -- on MOS drive circuit
Spire Office 7.5.4 for NET

Do you regret becoming a programmer?
随机推荐
When to use useImperativeHandle, useLayoutEffect, and useDebugValue
《牛客刷verilog》Part III Verilog企业真题
Research notes I software engineering and calculation volume II (Chapter 1-7)
Xinyuan & Lichuang EDA training camp - brushless motor drive
Which side projects can be achieved? Is it difficult for we media to earn more than 10000 a month?
用列表初始化你的vector&&initializer_list简介
How to enable relationship view in phpMyAdmin - how to enable relationship view in phpMyAdmin
Zero rhino technology joined hands with the intelligence Club: the "causal faction" forum was successfully held, and the "causal revolution" brought the next generation of trusted AI
LeetCode——Add Binary
Fiddler Everywhere 3.2.1 Crack
CIS benchmark tool Kube bench
My colleagues quietly told me that flying Book notification can still play like this
保研笔记四 软件工程与计算卷二(8-12章)
Rasa 3. X learning series -rasa 3.2.1 new release
C # input how many cards are there in each of the four colors.
有什么不起眼却挣钱的副业?
Bao Yan notes II software engineering and calculation volume II (Chapter 13-16)
21. PWM application programming
Scala concurrent programming (II) akka
Dynamic planning: robbing families and houses