当前位置:网站首页>LeetCode 1447. Simplest fraction
LeetCode 1447. Simplest fraction
2022-07-06 16:42:00 【Daylight629】
1447. Simplest fraction
Give you an integer n , Please return to all 0 To 1 Between ( barring 0 and 1) Satisfy that the denominator is less than or equal to n Of Simplest fraction . The score can be in the form of arbitrarily Sequential return .
Example 1:
Input :n = 2
Output :["1/2"]
explain :"1/2" Is the only denominator less than or equal to 2 The simplest fraction of .
Example 2:
Input :n = 3
Output :["1/2","1/3","2/3"]
Example 3:
Input :n = 4
Output :["1/2","1/3","1/4","2/3","3/4"]
explain :"2/4" It's not the simplest fraction , Because it can be reduced to "1/2" .
Example 4:
Input :n = 1
Output :[]
Tips :
1 <= n <= 100
Two 、 Method 1
class Solution {
public List<String> simplifiedFractions(int n) {
List<String> res = new ArrayList<>();
for (int i = 1; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
if(gcb(i, j) == 1) res.add(i + "/" + j);
}
}
return res;
}
// More derogation
public int gcb(int a, int b) {
while(true) {
if (a > b) a -= b;
else if (b > a) b -= a;
else return a;
}
}
}
Complexity analysis
- Time complexity : The complexity of enumerating numerators and denominators is O(n^2); The complexity of judging whether two numbers can be combined into the simplest fraction is O(logn). The overall complexity is O(n2∗logn)
- Spatial complexity : Ignore the extra space overhead caused by recursion , The complexity is O(1)
3、 ... and 、 Method 2
class Solution {
public List<String> simplifiedFractions(int n) {
List<String> res = new ArrayList<>();
for (int i = 1; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
if(gcb(i, j) == 1) res.add(i + "/" + j);
}
}
return res;
}
// Euclid algorithm
public int gcb(int a, int b) {
return b == 0 ? a : gcb(b, a % b);
}
}
Complexity analysis
- Time complexity : The complexity of enumerating numerators and denominators is O(n^2); The complexity of judging whether two numbers can be combined into the simplest fraction is O(logn). The overall complexity is O(n2∗logn)
- Spatial complexity : Ignore the extra space overhead caused by recursion , The complexity is O(1)
边栏推荐
- 第一章 MapReduce概述
- VMware Tools和open-vm-tools的安装与使用:解决虚拟机不全屏和无法传输文件的问题
- 业务系统从Oracle迁移到openGauss数据库的简单记录
- 字节跳动新程序员成长秘诀:那些闪闪发光的宝藏mentor们
- Problem - 922D、Robot Vacuum Cleaner - Codeforces
- Hbuilder X格式化快捷键设置
- Browser print margin, default / borderless, full 1 page A4
- It is forbidden to trigger onchange in antd upload beforeupload
- Codeforces Round #798 (Div. 2)A~D
- 生成随机密码/验证码
猜你喜欢
Problem - 922D、Robot Vacuum Cleaner - Codeforces
Solve the problem that intel12 generation core CPU single thread only runs on small cores
300th weekly match - leetcode
Oneforall installation and use
Install Jupiter notebook under Anaconda
Use JQ to realize the reverse selection of all and no selection at all - Feng Hao's blog

解决Intel12代酷睿CPU单线程只给小核运行的问题
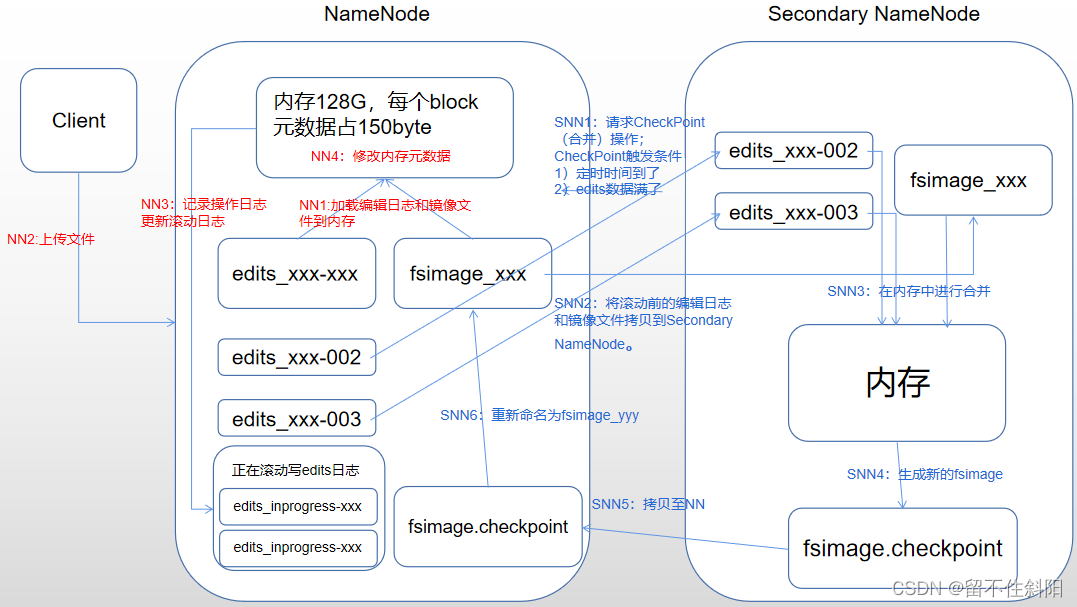
Chapter 5 namenode and secondarynamenode

Simply try the new amp model of deepfacelab (deepfake)
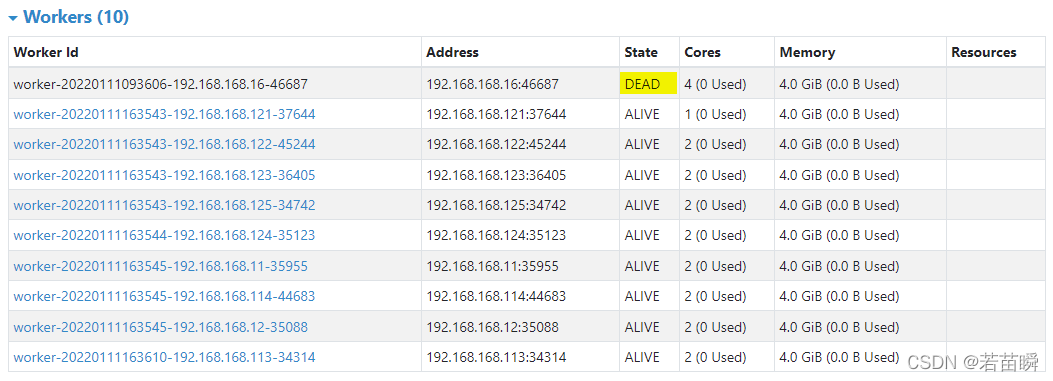
Spark独立集群动态上线下线Worker节点
随机推荐
力扣leetcode第 280 场周赛
Hbuilder x format shortcut key settings
第一章 MapReduce概述
简单尝试DeepFaceLab(DeepFake)的新AMP模型
(lightoj - 1349) Aladdin and the optimal invitation (greed)
Date plus 1 day
Audio and video development interview questions
第三章 MapReduce框架原理
MariaDB的安装与配置
第五章 Yarn资源调度器
生成随机密码/验证码
Research Report on hearing health care equipment industry - market status analysis and development prospect prediction
Use JQ to realize the reverse selection of all and no selection at all - Feng Hao's blog
Chapter 7__ consumer_ offsets topic
MP4格式详解
【锟斤拷】的故事:谈谈汉字编码和常用字符集
Acwing: Game 58 of the week
Chapter III principles of MapReduce framework
Codeforces Round #800 (Div. 2)AC
Spark独立集群Worker和Executor的概念