当前位置:网站首页>(lightoj - 1236) pairs forming LCM (prime unique decomposition theorem)
(lightoj - 1236) pairs forming LCM (prime unique decomposition theorem)
2022-07-06 16:23:00 【AC__ dream】
Topic link :Pairs Forming LCM - LightOJ 1236 - Virtual Judge
Chinese question meaning : Given a n Please lcm(a,b) Number to number ,lcm Represents the least common multiple , And (a,b) and (b,a) Treat as the same number pair .
analysis : set up n=p1^n1+p2^n2+……+pm^nm(m It's a subscript )
be a and b They can be expressed as
a=p1^a1+p2^a2+……+pm^am
b=p1^b1+p2^b2+……+bm^bm
Easy to know , if n=lcm(a,b), Then there are max(ai,bi)=ni, That is to say for n A qualitative factor of p,a and b contains p The maximum value of the power of the factor is equal to n contains p The power of the factor , That's for everyone pi factor ,ai and bi One of them must be ni, The other is 0~ni Any number in , So there is 2*(ni+1)-1=2*ni+1( Because both are ni It's a kind of emptying ), But contentment a<=b The number of cases except a=b=n This is not the case , Everything else is satisfaction a<b The number of cases is equal to a>b The number of cases , In addition to (n,n) Numbers other than this pair are divided by 2 that will do , That is to say (cal(n)-1)/2+1, Then add (n,n) In this case .
Here is the code :
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
const int N=1e7+9;
bool vis[N];
int prime[N],cnt;
void init()
{
for(int i=2;i<N;i++)
{
if(!vis[i]) prime[++cnt]=i;
for(int j=1;j<=cnt&&i*prime[j]<N;j++)
{
vis[i*prime[j]]=true;
if(i%prime[j]==0) break;
}
}
}
ll cal(ll n)
{
ll ans=1;
for(int i=1;i<=cnt&&prime[i]*prime[i]<=n;i++)
{
ll count=0;
while(n%prime[i]==0)
{
n/=prime[i];
count++;
}
ans*=(2*count+1);
}
if(n>1) ans*=(2*1+1);// also n This is the prime factor
return ans;
}
int main()
{
init();
int T;
cin>>T;
for(int _=1;_<=T;_++)
{
ll n;
scanf("%lld",&n);
printf("Case %d: %lld\n",_,cal(n)/2+1);
}
return 0;
}边栏推荐
- 第 300 场周赛 - 力扣(LeetCode)
- C language is the watershed between low-level and high-level
- Configuration du cadre flask loguru log Library
- 1529. Minimum number of suffix flips
- It is forbidden to trigger onchange in antd upload beforeupload
- Advancedinstaller安装包自定义操作打开文件
- Quick to typescript Guide
- Data storage in memory & loading into memory to make the program run
- AcWing:第56场周赛
- 860. Lemonade change
猜你喜欢
Write web games in C language
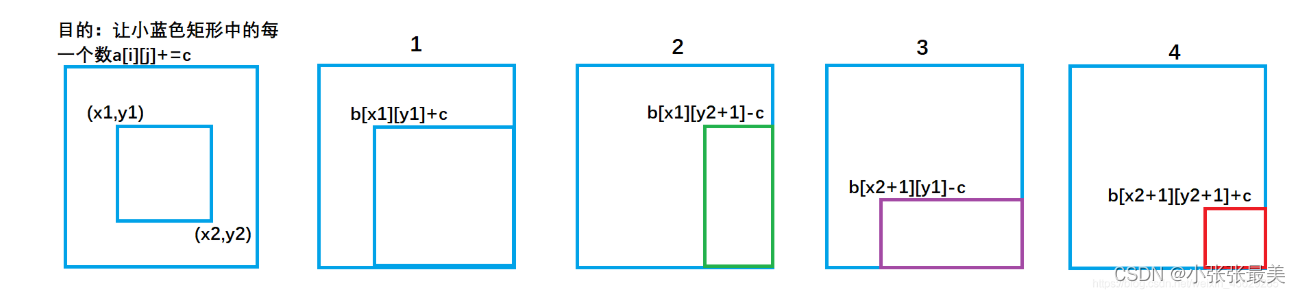
Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack
Codeforces Round #797 (Div. 3)无F
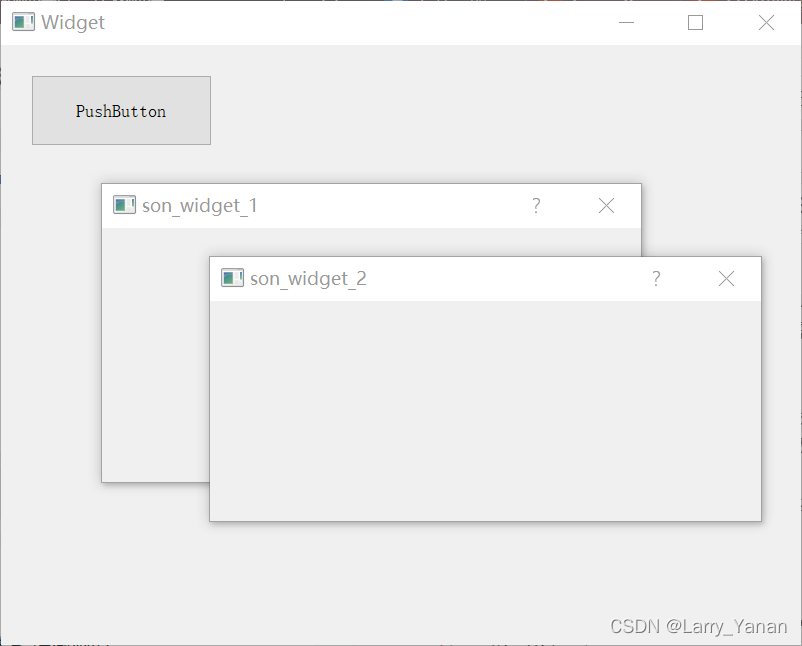
QT实现窗口置顶、置顶状态切换、多窗口置顶优先关系
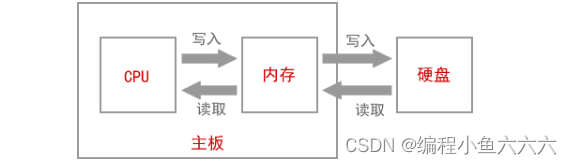
Data storage in memory & loading into memory to make the program run

Codeforces Round #799 (Div. 4)A~H
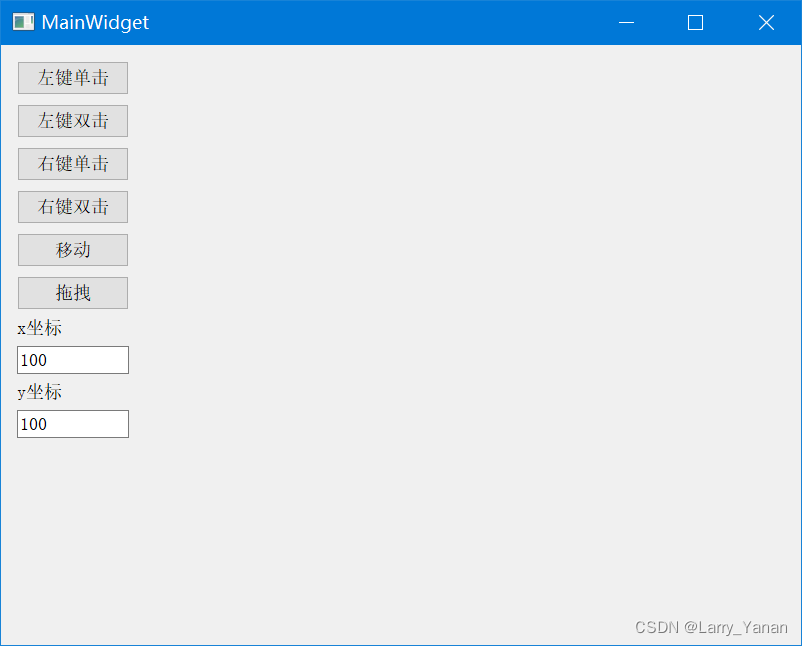
QT simulates mouse events and realizes clicking, double clicking, moving and dragging

B - Code Party (girls' competition)
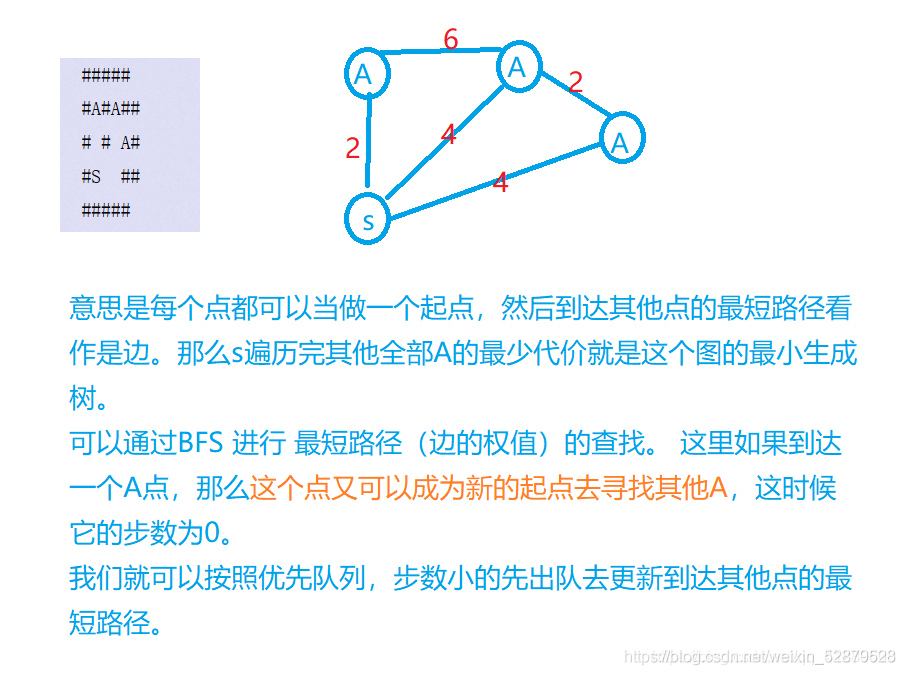
Borg maze (bfs+ minimum spanning tree) (problem solving report)
Frida hook so layer, protobuf data analysis
随机推荐
Classic application of stack -- bracket matching problem
window11 conda安装pytorch过程中遇到的一些问题
Codeforces Round #801 (Div. 2)A~C
QT implementation window gradually disappears qpropertyanimation+ progress bar
Codeforces Round #798 (Div. 2)A~D
QT按钮点击切换QLineEdit焦点(含代码)
Acwing: Game 58 of the week
875. Leetcode, a banana lover
Codeforces Round #803 (Div. 2)A~C
指定格式时间,月份天数前补零
<li>圆点样式 list-style-type
1605. Sum the feasible matrix for a given row and column
HDU - 6024 building shops (girls' competition)
1013. Divide the array into three parts equal to and
628. Maximum product of three numbers
Vs2019 initial use
Codeforces Round #800 (Div. 2)AC
树莓派4B64位系统安装miniconda(折腾了几天终于解决)
Basic Q & A of introductory C language
QWidget代码设置样式表探讨