Codeforces Round #801 (Div. 2)A~C

Problem - A - Codeforces

Michael and Joe are playing a game. The game is played on a grid with n rows and m columns, filled with distinct integers. We denote the square on the i-th (1≤i≤n) row and j-th (1≤j≤m) column by (i,j) and the number there by aij.

Michael starts by saying two numbers h (1≤h≤n) and w (1≤w≤m). Then Joe picks any h×w subrectangle of the board (without Michael seeing).

Formally, an h×w subrectangle starts at some square (a,b) where 1≤a≤n−h+1 and 1≤b≤m−w+1. It contains all squares (i,j) for a≤i≤a+h−1 and b≤j≤b+w−1.

Finally, Michael has to guess the maximum number in the subrectangle. He wins if he gets it right.

Because Michael doesn’t like big numbers, he wants the area of the chosen subrectangle (that is, h⋅w), to be as small as possible, while still ensuring that he wins, not depending on Joe’s choice. Help Michael out by finding this minimum possible area.

It can be shown that Michael can always choose h,w for which he can ensure that he wins.

Input

Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤20). Description of the test cases follows.

The first line of each test case contains two integers n and m (1≤n,m≤40) — the size of the grid.

Each of the following n lines contains m integers. The j-th integer on the i-th line is aij (−10^9≤aij≤10 9) — the element in the cell (i,j).

It is guaranteed that all the numbers are distinct (that is, if ai1j1=ai2j2, then i1=i2,j1=j2).

Output

For each test case print a single positive integer — the minimum possible area the subrectangle can have while still ensuring that Michael can guarantee the victory.

Example

input

3
1 1
3
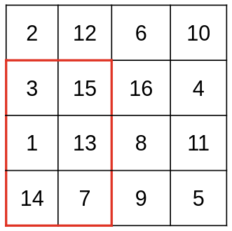
4 4
2 12 6 10
3 15 16 4
1 13 8 11
14 7 9 5
2 3
-7 5 2
0 8 -3

output

1
9
4

Problem analysis

The problem is that , Here's a matrix for you , You can ask a person to draw an area of x( Long * high ) The submatrix of , Then you can guess the maximum number in this matrix , Ask what is the smallest area of the submatrix that you can win safely .

Is to find the maximum value in the matrix , Then look at the coordinates of this value to the matrix area of the four corners , Take one of the biggest , In this way, we can ensure that no matter how the submatrix is taken , Must be able to make this maximum appear in the submatrix .

AC Code

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>

#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
    {
        int n, m;
        cin >> n >> m;
        ll mx = -1e10, res = 0;
        vector<vector<int>>v(n, vector<int>(m));
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
            {
                cin >> v[i][j];
                if (v[i][j] >= mx)
                {
                    int l_up = (i + 1) * (j + 1);
                    int r_up = (i + 1) * (m - j);
                    int l_down = (n - i) * (j + 1);
                    int r_down = (n - i) * (m - j);
                    res = max(max(l_up, r_up), max(l_down, r_down));
                    mx = v[i][j];
                }
            }
        }
        cout << res << endl;
    }
    return 0;
}

Problem - B - Codeforces

Mike and Joe are playing a game with some stones. Specifically, they have n piles of stones of sizes a1,a2,…,an. These piles are arranged in a circle.

The game goes as follows. Players take turns removing some positive number of stones from a pile in clockwise order starting from pile 1. Formally, if a player removed stones from pile i on a turn, the other player removes stones from pile ((imodn)+1) on the next turn.

If a player cannot remove any stones on their turn (because the pile is empty), they lose. Mike goes first.

If Mike and Joe play optimally, who will win?

Input

Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤1000). Description of the test cases follows.

The first line of each test case contains a single integer n (1≤n≤50) — the number of piles.

The second line contains n integers a1,a2,…,an (1≤ai≤10^ 9) — the size of the piles.

Output

For each test case print the winner of the game, either “Mike” or “Joe” on its own line (without quotes).

Example

input

2
1
37
2
100 100

output

Mike
Joe

Problem analysis

Says there is n Make stones , Each pile of stones has a[i] A stone , In limine mike Start with the first pile , You can take any number each time , The next person can only go to the first （i+1)%n Pile stones and take stones , If anyone can't get the stone first , Who is lost . Ask who can win in the end .

If the stones are odd , Then just take it every time , When Joe When you go back to the beginning of the queue, you will lose without a stone , therefore n The odd number is mike It will win .

If it's even , that mike I always take odd stones ,joe It's an even number of stones . That is, who takes any stone pile in his queue first , He lost , So let's compare how many stones there are in the least number of stone piles on both sides , The least one loses , If the same , Just look at the pile in front , Lose in front .

AC Code

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>

#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
    {
        int n;
        cin >> n;
        vector<int>v(n);
        for (int i = 0; i < n; i++)cin >> v[i];
        if (n % 2 == 1)
        {
            cout << "Mike" << endl;
            continue;
        }
        int mn_j = 1e18, mn_o = 1e18, pos_j = -1, pos_o = -1;
        for (int i = 0; i < n; i += 2)
        {
            if (mn_j > v[i])
            {
                mn_j = v[i];
                pos_j = i;
            }
        }
        for (int i = 1; i < n; i += 2)
        {
            if (mn_o > v[i])
            {
                mn_o = v[i];
                pos_o = i;
            }
        }
        if (mn_j<mn_o||(mn_j==mn_o&&pos_j<pos_o))cout << "Joe" << endl;
        else cout << "Mike" << endl;
    }
    return 0;
}

Problem - C - Codeforces

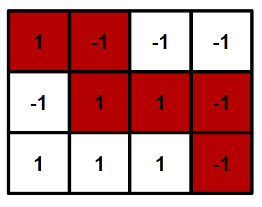
You are given a grid with n rows and m columns. We denote the square on the i-th (1≤i≤n) row and j-th (1≤j≤m) column by (i,j) and the number there by aij. All numbers are equal to 1 or to −1.

You start from the square (1,1) and can move one square down or one square to the right at a time. In the end, you want to end up at the square (n,m).

Is it possible to move in such a way so that the sum of the values written in all the visited cells (including a11 and anm) is 0?

Input

Each test contains multiple test cases. The first line contains the number of test cases t (1≤t≤104). Description of the test cases follows.

The first line of each test case contains two integers n and m (1≤n,m≤1000) — the size of the grid.

Each of the following n lines contains m integers. The j-th integer on the i-th line is aij (aij=1 or −1) — the element in the cell (i,j).

It is guaranteed that the sum of n⋅m over all test cases does not exceed 106.

Output

For each test case, print “YES” if there exists a path from the top left to the bottom right that adds up to 0, and “NO” otherwise. You can output each letter in any case.

Example

input

5
1 1
1
1 2
1 -1
1 4
1 -1 1 -1
3 4
1 -1 -1 -1
-1 1 1 -1
1 1 1 -1
3 4
1 -1 1 1
-1 1 -1 1
1 -1 1 1

output

NO
YES
YES
YES
NO

Problem analysis

The title is to give you a matrix , Only by 1 and -1 form , Start from the upper left corner , You can only go right and down , Ask if you can find a way to make the sum of this road 0.

First , Length of matrix n And width m Addition must be odd , If it's even , Then there will be odd numbers on the path , It is impossible for 0 Of .

Then we can directly find out the maximum and minimum values of walking from the top left to sitting down , As long as the range formed by the maximum and minimum values can include 0, Then you can find a way out , Not vice versa .

AC Code

#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>

#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;
int n, m;

signed main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
    {
        cin >> n >> m;
        vector<vector<int>>v(n, vector<int>(m)), f(n, vector<int>(m));
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < m; j++)
                cin >> v[i][j];
        }
        if ((n+m)%2==0)
        {
            cout << "NO" << endl;
            continue;
        }
        
        int mn = v[0][0], mx = v[0][0];
        f[0][0] = v[0][0];
        for (int i = 1; i < n; i++)
        {
            f[i][0] = f[i - 1][0] + v[i][0];
        }
        for (int j = 1; j < m; j++)
        {
            f[0][j] = f[0][j - 1] + v[0][j];
        }

        for (int i = 1; i < n; i++)
        {
            for (int j = 1; j < m; j++)
            {
                f[i][j] = max(f[i - 1][j], f[i][j - 1]) + v[i][j];
            }
        }
        mx = f[n - 1][m - 1];
        for (int i = 1; i < n; i++)
        {
            for (int j = 1; j < m; j++)
            {
                f[i][j] = min(f[i - 1][j], f[i][j - 1]) + v[i][j];
            }
        }
        mn = f[n - 1][m - 1];

        if (mx >= 0 && mn <= 0)cout << "YES" << endl;
        else cout << "NO" << endl;
    }
    return 0;
}