当前位置:网站首页>Codeforces Round #800 (Div. 2)AC
Codeforces Round #800 (Div. 2)AC
2022-07-06 09:28:00 【你好_Ä】
Codeforces Round #800 (Div. 2)A~C
Problem - A - Codeforces
Define the score of some binary string TT as the absolute difference between the number of zeroes and ones in it. (for example, T=T= 010001 contains 44 zeroes and 22 ones, so the score of TT is |4−2|=2|4−2|=2).
Define the creepiness of some binary string SS as the maximum score among all of its prefixes (for example, the creepiness of S=S= 01001 is equal to 22 because the score of the prefix S[1…4]S[1…4] is 22 and the rest of the prefixes have a score of 22 or less).
Given two integers aa and bb, construct a binary string consisting of aa zeroes and bb ones with the minimum possible creepiness.
Input
The first line contains a single integer tt (1≤t≤1000)(1≤t≤1000) — the number of test cases. The description of the test cases follows.
The only line of each test case contains two integers aa and bb (1≤a,b≤1001≤a,b≤100) — the numbers of zeroes and ones correspondingly.
Output
For each test case, print a binary string consisting of aa zeroes and bb ones with the minimum possible creepiness. If there are multiple answers, print any of them.
Example
input
5
1 1
1 2
5 2
4 5
3 7
output
10
011
0011000
101010101
0001111111
问题解析
这题是说,一个字符串只由01组成,这个字符串的分数是0的个数和1的个数的差值,这个字符串的威胁程度是它的所有子串的最大分数,给你a个0和b个1,组成一个字符串,让他的威胁程度最低。
只要把01交替输出即可,多出来的再放到结尾输出。
AC代码
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int t;
cin >> t;
while (t--)
{
int a, b;
cin >> a >> b;
if (a > b)
{
for (int i = 0; i < b; i++)cout << "01";
for (int i = 0; i < a - b; i++)cout << 0;
}
else
{
for (int i = 0; i < a; i++)cout << "10";
for (int i = 0; i < b - a; i++)cout << 1;
}
cout << endl;
}
return 0;
}
Problem - B - Codeforces
Let’s call a binary string T of length m indexed from 1 to m paranoid if we can obtain a string of length 1 by performing the following two kinds of operations m−1 times in any order :
Select any substring of T that is equal to 01, and then replace it with 1.
Select any substring of T that is equal to 10, and then replace it with 0.
For example, if T= 001, we can select the substring [T2T3] and perform the first operation. So we obtain T= 01.
You are given a binary string S of length n indexed from 1 to n. Find the number of pairs of integers (l,r) 1≤l≤r≤n such that S[l…r] (the substring of S from l to r) is a paranoid string.
Input
The first line contains an integer t (1≤t≤1000) — the number of test cases. The description of test cases follows.
The first line of each test case contains a single integer n (1≤n≤2⋅105) — the size of S.
The second line of each test case contains a binary string S of n characters S1S2…Sn. (Si= 0 or Si= 1 for each 1≤i≤n)
It is guaranteed that the sum of n over all test cases doesn’t exceed 2⋅105.
Output
For each test case, output the number of pairs of integers (l,r) 1≤l≤r≤n such that S[l…r] (the substring of S from l to r) is a paranoid string.
Example
input
5
1
1
2
01
3
100
4
1001
5
11111
output
1
3
4
8
5
问题解析
提示是说给你一个字符串,只由0和1组成,有两种操作,可以把一个子串“01”变成“1”,“10”变成“0”,问这个字符串有多少个子串可以通过这个两个操作变成一个字符。
可以看出,只要结尾是“11”或“00”组成的字符串都不可能变成一个字符。我们只要找出以这两个为结尾的子串就行,然后用所有的子串数减去这个特殊的子串数即可。
AC代码
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int t;
cin >> t;
while (t--)
{
int n;
string s;
cin >> n >> s;
int res = 0;
for (int i = 0; i < n - 1; i++)
{
if (s[i] == '0' && s[i + 1] == '0')res += i+1;
if (s[i] == '1' && s[i + 1] == '1')res += i+1;
}
cout << n * (n + 1) / 2 - res << endl;
}
return 0;
}
Problem - C - Codeforces
We have an array of length n. Initially, each element is equal to 0 and there is a pointer located on the first element.
We can do the following two kinds of operations any number of times (possibly zero) in any order:
If the pointer is not on the last element, increase the element the pointer is currently on by 1. Then move it to the next element.
If the pointer is not on the first element, decrease the element the pointer is currently on by 1. Then move it to the previous element.
But there is one additional rule. After we are done, the pointer has to be on the first element.
You are given an array a. Determine whether it’s possible to obtain a after some operations or not.
Input
The first line contains a single integer t (1≤t≤1000) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer n (1≤n≤2⋅105) — the size of array a.
The second line of each test case contains n integers a1,a2,…,an (−109≤ai≤109) — elements of the array.
It is guaranteed that the sum of n over all test cases doesn’t exceed 2⋅105.
Output
For each test case, print “Yes” (without quotes) if it’s possible to obtain a after some operations, and “No” (without quotes) otherwise.
You can output “Yes” and “No” in any case (for example, strings “yEs”, “yes” and “Yes” will be recognized as a positive response).
Example
input
7
2
1 0
4
2 -1 -1 0
4
1 -4 3 0
4
1 -1 1 -1
5
1 2 3 4 -10
7
2 -1 1 -2 0 0 0
1
0
output
No
Yes
No
No
Yes
Yes
Yes
问题解析
题目是说有一个长度为n的数组,一开始元素全为0,然后有两种操作,如果当前指针不在最后一个元素,那么可以使这个元素+1后移动到后面,如果不在第一个元素,可以使这个元素-1后向前移动。给你一个数组a,问你能不能把这个初始数组变成a,而且之后指针要指向第一个元素。
首先可以知道,最后一个非0元素必然是负数,因为要从后往前走必须要减去1,而想加1则需要往后走,但最后一个非0元素显然是没有向后走过,只能向前,那么就不可能是负数;同理可知道第一个元素只能是正数。
然后我们也可以知道,一个数如果往前,必然是后面的数-1了,一个数想要增加那对应的后面的数就要减小,而因为指针最后停在第一位,相当于这一趟出去向左走和向右走的次数是相等的,即整个数组的总和应该是0,表现为前缀和的话就是从开头到最后一个非0数的前缀和是0,其余位置的前缀和不可能小于等于0,如果小于0,那么这个位置走不回第一个位置。如果等于0,那么他做不到向后走。
所以结论就是:数组的第一个元素必须是正数,最后一个数非0数必须为负,前前缀和除了到最后一个非0数位置的前缀和为0,前面位置的前缀和都必须大于0。
AC代码
#include<iostream>
using namespace std;
#include<vector>
#include<algorithm>
#include<math.h>
#include<set>
#include<numeric>
#include<string>
#include<string.h>
#include<iterator>
#include<map>
#include<unordered_map>
#include<stack>
#include<list>
#include<queue>
#include<iomanip>
#define endl '\n'
#define int ll
typedef long long ll;
typedef unsigned long long ull;
typedef pair<ll, ll>PII;
const int N = 2e5 + 50;
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int t;
cin >> t;
while (t--)
{
int n, res = 0;
cin >> n;
vector<int>v(n);
for (int i = 0; i < n; i++)
{
cin >> v[i];
}
while (!v.empty() && v.back() == 0)v.pop_back();
n = v.size();
bool flag = true;
for (int i = 0; i < n; i++)
{
res += v[i];
if (i != n - 1 && res <= 0)
{
flag = false;
break;
}
}
if (res != 0)
{
flag = false;
}
if (!flag)cout << "No" << endl;
else cout << "Yes" << endl;
}
return 0;
}
边栏推荐
- [exercise-6] (PTA) divide and conquer
- F - birthday cake (Shandong race)
- Information security - security professional name | CVE | rce | POC | Vul | 0day
- 【练习-1】(Uva 673) Parentheses Balance/平衡的括号 (栈stack)
- Information security - Analysis of security orchestration automation and response (soar) technology
- MySQL grants the user the operation permission of the specified content
- Analyse du format protobuf du rideau en temps réel et du rideau historique de la station B
- Penetration testing (5) -- a collection of practical skills of scanning King nmap and penetration testing tools
- 渗透测试 ( 2 ) --- 渗透测试系统、靶机、GoogleHacking、kali工具
- Information security - Epic vulnerability log4j vulnerability mechanism and preventive measures
猜你喜欢
Penetration test (8) -- official document of burp Suite Pro
1689. Ten - the minimum number of binary numbers
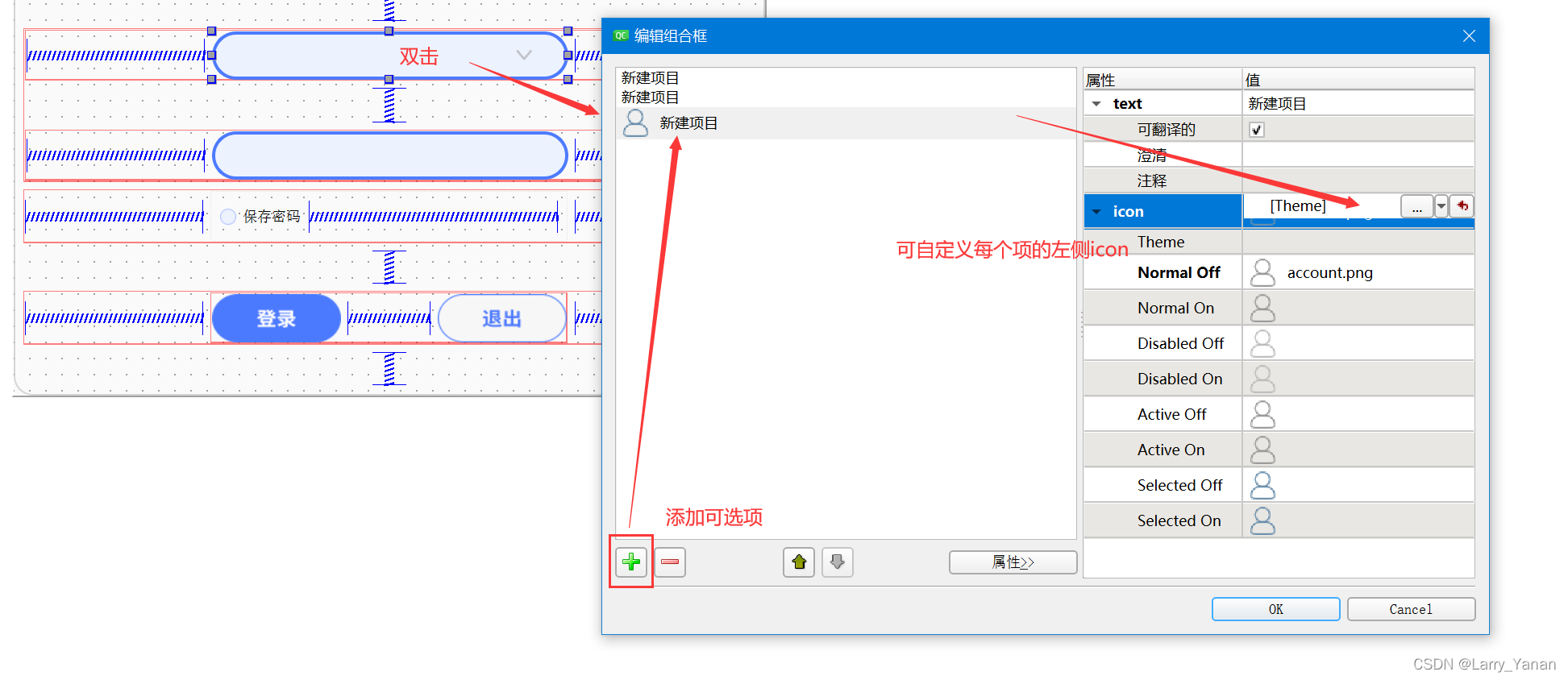
QT有关QCobobox控件的样式设置(圆角、下拉框,向上展开、可编辑、内部布局等)
![[exercise-4] (UVA 11988) broken keyboard = = (linked list)](/img/59/78ca7170ab1fd364ec44cfbcdc7ab5.png)
[exercise-4] (UVA 11988) broken keyboard = = (linked list)
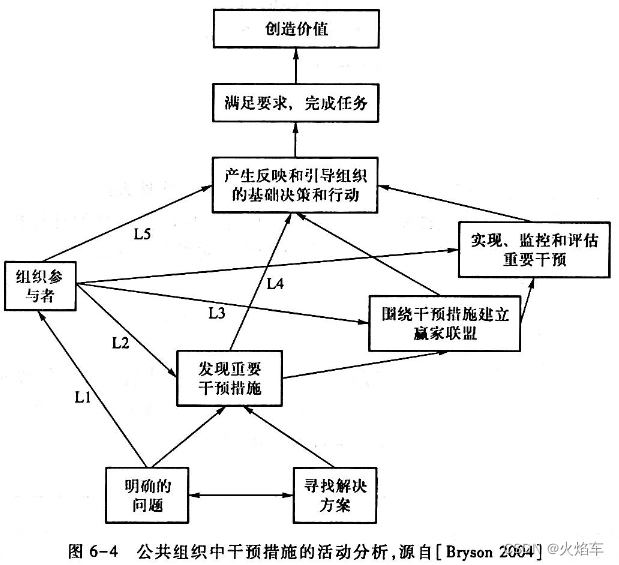
【高老师软件需求分析】20级云班课习题答案合集
![MySQL import database error [err] 1273 - unknown collation: 'utf8mb4_ 0900_ ai_ ci’](/img/e6/f4a696179282fe1f4193410c5a493a.png)
MySQL import database error [err] 1273 - unknown collation: 'utf8mb4_ 0900_ ai_ ci’

Penetration testing (5) -- a collection of practical skills of scanning King nmap and penetration testing tools
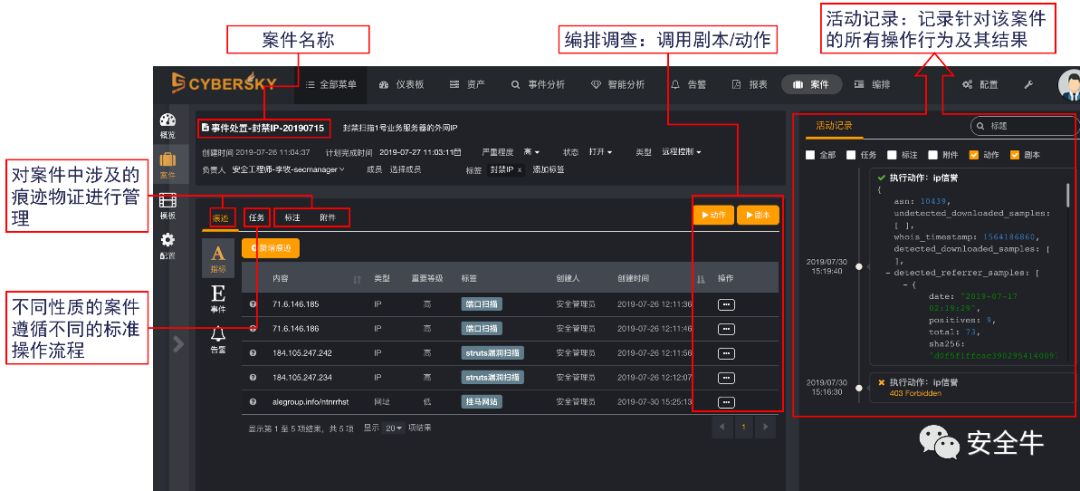
信息安全-安全编排自动化与响应 (SOAR) 技术解析
![[exercise-5] (UVA 839) not so mobile (balance)](/img/8e/48dcf75f7347b36301df6fc129c09d.png)
[exercise-5] (UVA 839) not so mobile (balance)
2027. Minimum number of operations to convert strings
随机推荐
【练习-3】(Uva 442)Matrix Chain Multiplication(矩阵链乘)
树莓派4B安装opencv3.4.0
[teacher Gao UML software modeling foundation] collection of exercises and answers for level 20 cloud class
Analysis of protobuf format of real-time barrage and historical barrage at station B
[analysis of teacher Gao's software needs] collection of exercises and answers for level 20 cloud class
Essai de pénétration (1) - - outils nécessaires, navigation
Maximum product (greedy)
渗透测试 ( 7 ) --- 漏洞扫描工具 Nessus
QT有关QCobobox控件的样式设置(圆角、下拉框,向上展开、可编辑、内部布局等)
Auto.js入门
Perform general operations on iptables
Web based photo digital printing website
TCP's three handshakes and four waves
JS call camera
F - birthday cake (Shandong race)
渗透测试 ( 3 ) --- Metasploit Framework ( MSF )
【高老师UML软件建模基础】20级云班课习题答案合集
渗透测试 ( 4 ) --- Meterpreter 命令详解
409. Longest palindrome
渗透测试 ( 2 ) --- 渗透测试系统、靶机、GoogleHacking、kali工具