当前位置:网站首页>F - True Liars (种类并查集+DP)
F - True Liars (种类并查集+DP)
2022-07-06 06:08:00 【RCyyds】
传送门: True Liars


题意:给出n对关系,p1个好人,p2个坏人。要求根据n对关系中找出好人有哪些,若方案唯一,则逐个输出好人,最后输出end;若方案不唯一/找不到,那么输出no
思路:第一次碰到这种类型的题目,想了很久没什么思路,参考了其他人的博客才弄懂了。
以下为所参考博客的思路:
通过简单的分析可以得出,对于每对关系(x,y,yes/no),若关系为yes,则x和y属于同一类人;若关系为no,则x和y属于相反类人。
根据初步的n对关系,我们只可以推出哪些属于同一类人,哪些属于相反类人,但不可以确定到底哪类是好人/坏人。我们可以将相反的两类人确定为一个大集合,那么大集合里面就有两个小集合。根据题意,我们只需要从每个大集合中,选其中一个小集合,使得选中的所有小集合的人数总和为p1即可。
代码:
#include <cstdio>
#include <cstring>
#include <iostream>
#define MAXN 600
using namespace std;
int parent[MAXN], path[MAXN][MAXN], dp[MAXN][MAXN];
int num[MAXN]; //记录大集合的根节点为i的是第num[i]个大集合
int flag[MAXN][2]; //标记每个大集合中选中到最终结果的小集合
int cnt[MAXN][2]; //根节点为i时,分别记录两个小集合包含的人数
int relat[MAXN];
/* relation
* relat=0/1。0表示i和根节点parent[i]相关联,即属于同一个小集合;1表示i和根节点不关联,即属于同一个大集合中的不同小集合*/
int find(int x) {
if (x != parent[x]) { //此处的parent[x]是旧父
int px = find(parent[x]); // px是新父
relat[x] ^= relat[parent[x]];
/* 由于路径压缩要将x的父亲节点直接指向根节点,即更改了x的父亲节点,所以要更新节点x和根节点的关系。
*/
parent[x] = px;
}
return parent[x];
}
/*
对于"relat[x] ^= relat[parent[x]];"异或解释:
可以通过简单的分析得出:
1.如果( relation[x和旧父]=0 && relation[旧父和新父]=0 )或者(
relation[x和旧父]=1 && relation[旧父和新父]=1 ),则 relation[x和新父]=0
2.如果(relation[x和旧父]=1 && relation[旧父和新父]=0 )或者(
relation[x和旧父]=0 && relation[旧父和新父]=1 ),则 relation[x和新父]=1
可以发现,最终relatino[x和新父] = relation[x和旧父] ^ relation[旧父和新父]
即: relat[x] ^= relat[parent[x]];
对于下面的merge函数中的异或同理
*/
void merge(int x, int y, int d) { // d要么为0,要么为1
int px = find(x);
int py = find(y);
if (px != py) {
parent[py] = px;
relat[py] = relat[x] ^ relat[y] ^ d;
}
}
int main(void) {
int m, p, q;
while (scanf("%d%d%d", &m, &p, &q)) {
if (m + p + q == 0) {
break;
}
for (int i = 1; i <= p + q; i++) { //**初始话
relat[i] = 0;
parent[i] = i;
}
while (m--) {
int x, y, d = 1;
char ch[5];
scanf("%d%d%s", &x, &y, ch);
if (ch[0] == 'y') {
d = 0;
}
merge(x, y, d);
}
memset(num, 0, sizeof(num)); //**num存储集合个数并且给他们编号
memset(path, 0, sizeof(path));
memset(cnt, 0, sizeof(cnt));
memset(dp, 0, sizeof(dp));
memset(flag, 0, sizeof(flag));
int tot = 0;
for (int i = 1; i <= p + q; i++) { //**统计集合个数并且编号
if (find(i) == i) {
num[i] = ++tot; // tot连通块个数,num记录root=i的连通块的编号
}
}
for (int i = 1; i <= p + q;
i++) { //**分别统计每个集合两种类的数目并存储到cnt中
cnt[num[find(i)]][relat[i]]++;
}
dp[0][0] = 1;
for (int i = 1; i <= tot; i++) { // tot=2
for (int j = 0; j <= p+q; j++) { // p+q=7
//**dp[i][j]存储到第i个集合选择种类和为j的方法数
if (j - cnt[i][0] >= 0 && dp[i - 1][j - cnt[i][0]]) {
dp[i][j] += dp[i - 1][j - cnt[i][0]];
path[i][j] =
cnt[i][0]; //**path数组记录路径,即选的是1还是0
}
if (j - cnt[i][1] >= 0 && dp[i - 1][j - cnt[i][1]]) {
dp[i][j] += dp[i - 1][j - cnt[i][1]];
path[i][j] = cnt[i][1];
}
}
}
/*
这部分两个if有点难理解,因为可能会想到,两个if都满足的话,那么最后得出的dp[i][j]就有可能存在同一个大集合里面选取了两个小集合的情况,这样就违背了“只从一个大集合选其中一个小集合”的情况。但,可以发现,我们最后限制了方法数是dp[tot][p]=1时,才是有唯一方案的。如果像刚刚说的两个if都满足,那么dp[i][j]一定>1,也就不会符合下面的dp[tot][p]=1限制,所以解决了这个问题。
*/
if (dp[tot][p] != 1) {
printf("no\n");
} else {
for (int i = tot, j = p; j > 0 && i > 0; i--) { //**标记路径
if (path[i][j] == cnt[i][0]) {
flag[i][0] = 1;
} else {
flag[i][1] = 1;
}
j -= path[i][j];
//记得减。因为背包时恰好选够p,所以要跟随着p逐次减少当时的物品,找到路径
}
for (int i = 1; i <= p + q; i++) {
if (flag[num[find(i)]][relat[i]]) {
printf("%d\n", i);
}
}
printf("end\n");
}
}
return 0;
}
边栏推荐
猜你喜欢

Wib3.0 leapfrogging, in leapfrogging (ง • ̀_•́) ง
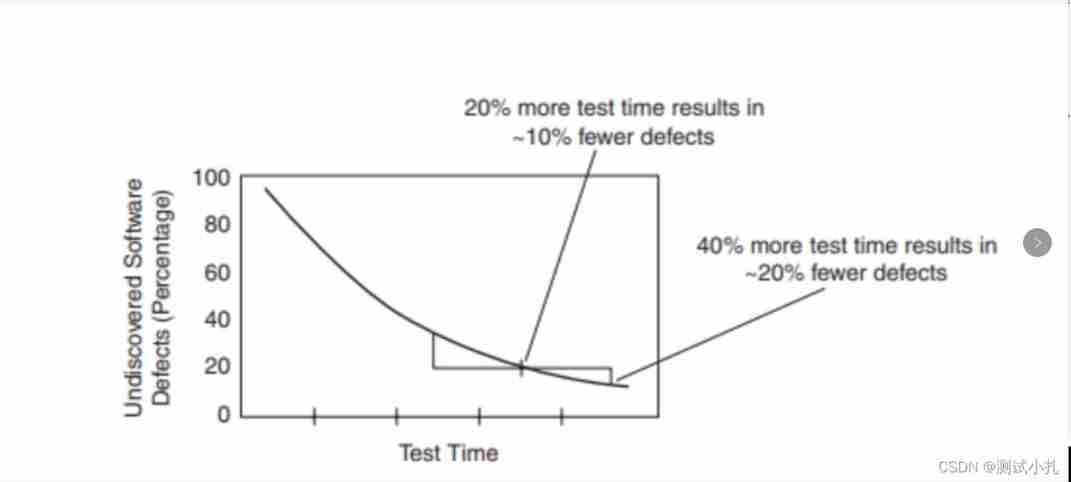
Seven imperceptible truths in software testing
![[Thesis code] SML part code reading](/img/3c/0deccf499d9b1cbe30a302cb115d73.png)
[Thesis code] SML part code reading

HCIA review

Manhattan distance sum - print diamond

Novice entry SCM must understand those things

Grant Yu, build a web page you want from 0
Nodejs realizes the third-party login of Weibo
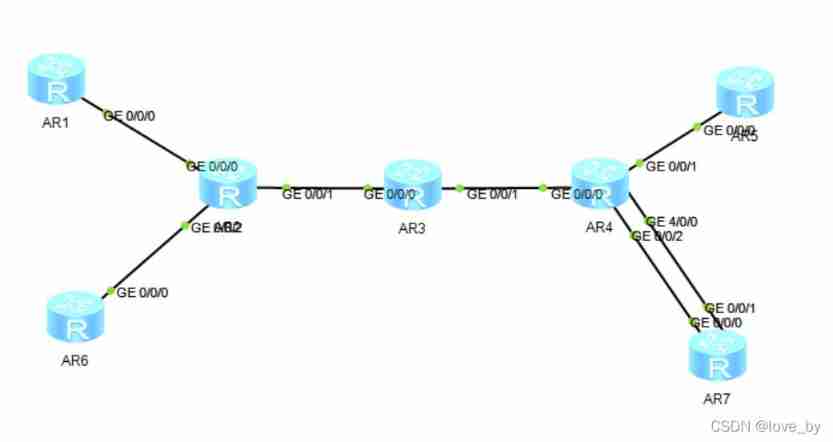
MPLS test report
![Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)](/img/c9/56fba6054c91f090de31463a8b4705.jpg)
Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)
随机推荐
Redis6 cluster setup
Commodity price visualization
Cognitive introspection
黑猫带你学eMMC协议第10篇:eMMC读写操作详解(read & write)
[course notes] Compilation Principle
leaflet 地图
Investment strategy discussion and market scale prediction report of China's solid state high power amplifier industry from 2022 to 2028
多线程应用的测试与调试
【C语言】qsort函数
selenium源码通读·9 |DesiredCapabilities类分析
Introduction to promql of # yyds dry goods inventory # Prometheus
【无App Push 通用测试方案
【C语言】字符串左旋
Testing and debugging of multithreaded applications
技术分享 | 常见接口协议解析
Reading notes of effective managers
Dynamic programming -- knapsack problem
一文揭开,测试外包公司的真 相
公司視頻加速播放
H3C V7 switch configuration IRF