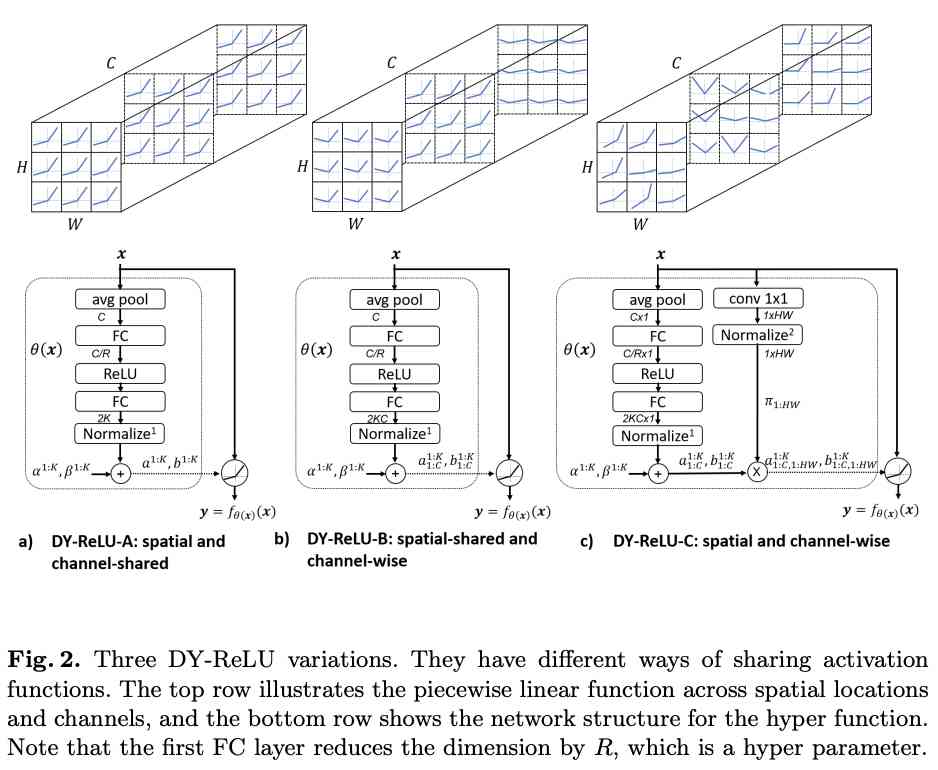
After reading this article , You can go and get the following questions :
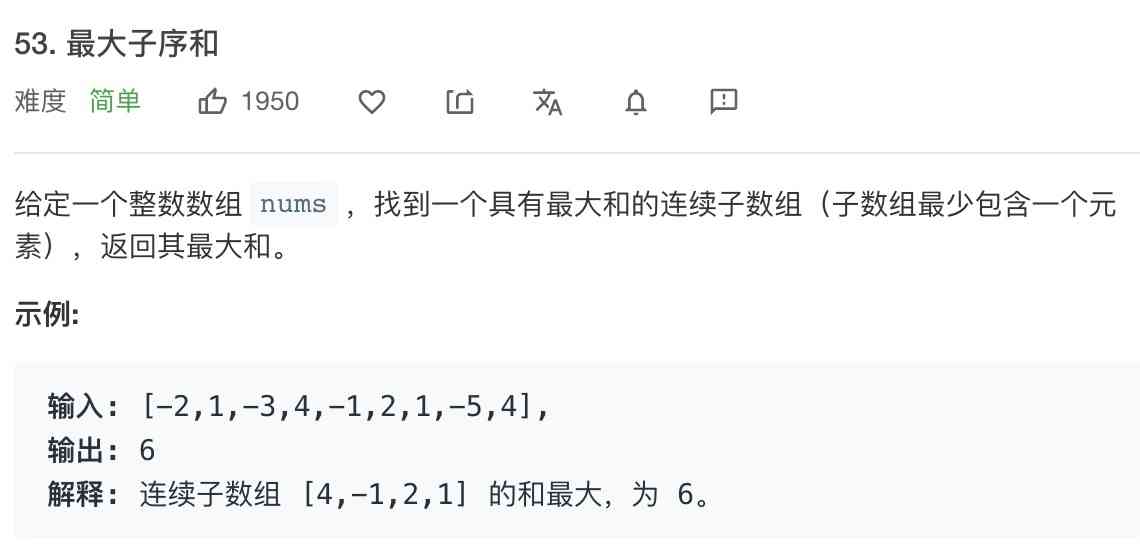
53. The largest subsequence and
-----------
The problem of the largest subarray is the same as the one mentioned above Classic dynamic planning : The longest increasing subsequence It's very similar , It represents a special dynamic programming problem :
Thought analysis
In fact, the first time I saw this problem , The first thing that came to my mind Sliding window algorithm , Because we said before , Sliding window algorithm is to deal with substring / Subarray problem , This is the subarray problem ?
however , A little analysis reveals that , This problem can't be solved by sliding window algorithm , Because the numbers in the array can be negative .
Sliding window algorithm is nothing more than a double pointer window scanning the entire array / Substring , But the point is , You have to know exactly when to move the right pointer to enlarge the window , When to move the left pointer to decrease the window .
And for this subject , Do you think , When the window expands, you may encounter negative numbers , The values in the window may increase or decrease , In this case, I don't know when to shrink the left window , It's impossible to find out 「 Maximum subarray and 」.
Solving this problem requires dynamic planning skills , however dp The definition of array is special . According to our conventional dynamic planning idea , It is generally defined as dp Array :
nums[0..i] Medium 「 The largest subarray and 」 by dp[i].
If so defined , Whole nums Array of 「 Maximum subarray and 」 Namely dp[n-1]. How to find the state transition equation ? According to mathematical induction , Suppose we know dp[i-1], How to deduce dp[i] Well ?
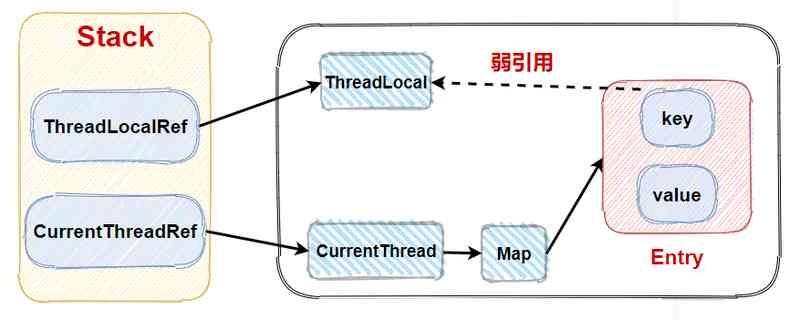
Here's the picture , According to what we said just now dp Definition of array ,dp[i] = 5 , It's equal to nums[0..i] The largest subarray in and :
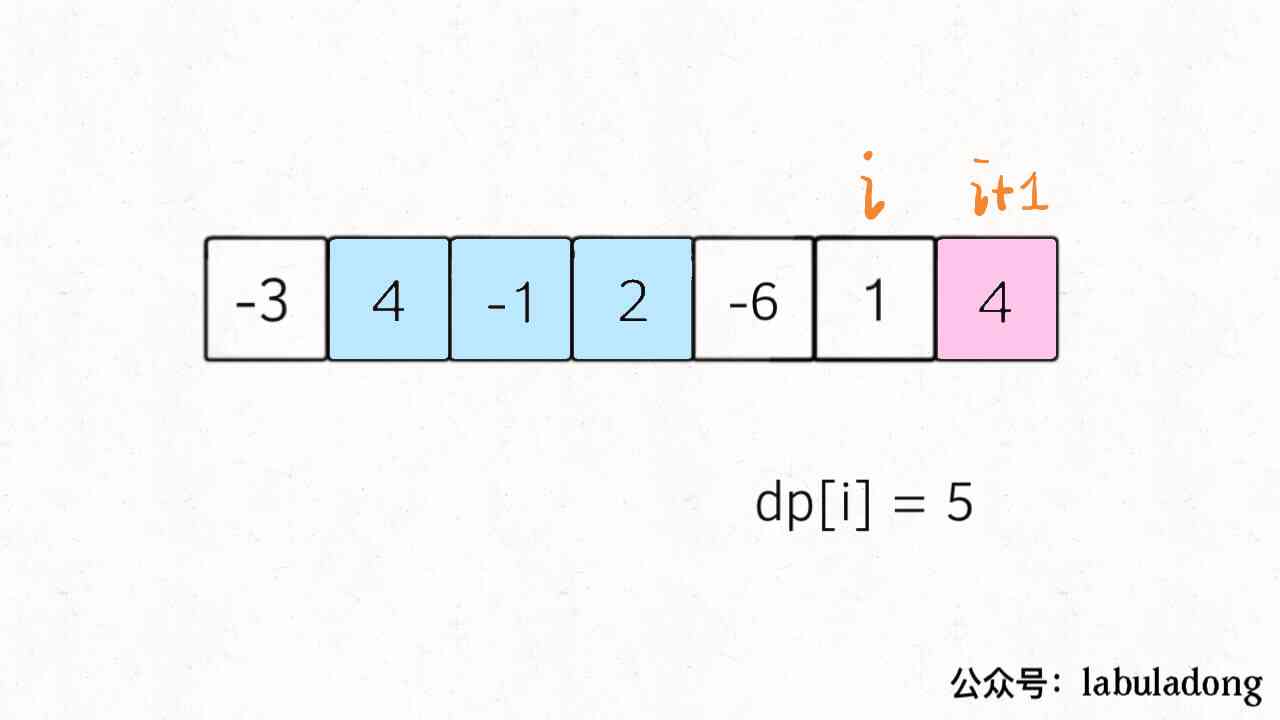
So in the case above , Using mathematical induction , You can use dp[i] Introduction dp[i+1] Do you ?
Not really , Because subarrays must be continuous , According to our current dp To define an array , There's no guarantee nums[0..i] The largest subarray in and nums[i+1] It's adjacent , There's no way to get from dp[i] Deduce dp[i+1].
So we define it this way dp The array is not correct , We can't get a proper state transition equation . For this kind of subarray problem , We're going to redefine dp The meaning of array :
With nums[i] For the end of 「 Maximum subarray and 」 by dp[i].
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
Under this definition , Want the whole thing nums Array of 「 Maximum subarray and 」, Cannot return directly dp[n-1], And you need to traverse the whole thing dp Array :
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
res = Math.max(res, dp[i]);
}
return res;
Still using mathematical induction to find state transition relations : Suppose we have worked out dp[i-1], How to deduce dp[i] Well ?
It can be done ,dp[i] There are two kinds of 「 choice 」, Or join to the previous adjacent subarray , Form a subarray of and larger ; Or not linked to the previous subarray , A school of its own , Self as a subarray .
How to choose ? Since it is required that 「 Maximum subarray and 」, Of course, choose the bigger one :
// Or it's a school of its own , Or merge with the previous subarray
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
Sum up , We've written the state transition equation , You can write the solution directly :
int maxSubArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
int[] dp = new int[n];
// base case
// There is no subarray before the first element
dp[0] = nums[0];
// State transition equation
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
}
// obtain nums The largest subarray of
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
The time complexity of the above solution is O(N), The complexity of space is also O(N), It's better than brute force , however be aware dp[i] Just and dp[i-1] The state of , So we can do 「 State compression 」, Reduce space complexity :
int maxSubArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
// base case
int dp_0 = nums[0];
int dp_1 = 0, res = dp_0;
for (int i = 1; i < n; i++) {
// dp[i] = max(nums[i], nums[i] + dp[i-1])
dp_1 = Math.max(nums[i], nums[i] + dp_0);
dp_0 = dp_1;
// By the way, calculate the largest result
res = Math.max(res, dp_1);
}
return res;
}
The final summary
Although the state transition equation derived from dynamic programming is more metaphysical , But most of them have some rules to follow .
Today this 「 Maximum subarray and 」 Just like 「 The longest increasing subsequence 」 Very similar ,dp The definition of an array is 「 With nums[i] Is the largest subarray at the end and / The longest increasing subsequence is dp[i]」. Because only in this way can we define dp[i+1] and dp[i] Build a connection , Using mathematical induction to write the state transition equation .
_____________
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ! Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star !