LeetCode 1552. Magnetic force between two balls

1552. The magnetic force between the two balls

Under the code name C-137 On the earth ,Rick Found that if he put two balls in his newly invented basket , There will be a special form of magnetic force between them .Rick Yes n An empty basket , The first i The position of the basket is position[i] ,Morty Want to put m Put a ball in these baskets , Between any two balls Minimum magnetic force Maximum .

It is known that if two balls are located at x and y , Then the magnetic force between them is |x - y| .

Give you an array of integers position And an integer m , Please return to maximize the minimum magnetic force .

Example 1：

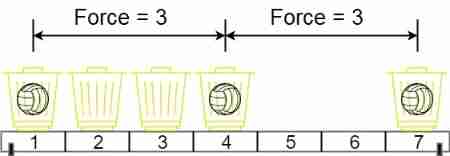
 Input ：position = [1,2,3,4,7], m = 3
 Output ：3
 explain ： take  3  Put the balls in the  1,4  and  7  The three baskets , The magnetic force between the two balls is  [3, 3, 6]. The minimum magnetic force is  3 . We can't make the minimum magnetic force greater than  3 .

Example 2：

 Input ：position = [5,4,3,2,1,1000000000], m = 2
 Output ：999999999
 explain ： We use the  1  and  1000000000  The basket has the minimum magnetic force and the maximum .

Tips ：

• n == position.length
• 2 <= n <= 10^5
• 1 <= position[i] <= 10^9
• all position The integer Different from each other .
• 2 <= m <= position.length

Two 、 Method 1

Two points search

class Solution {
    
    public int maxDistance(int[] position, int m) {
    
        Arrays.sort(position);
        int l = 1;
        int r = position[position.length - 1] - position[0];
        int res = -1;
        while (l <= r) {
    
            int mid = l + ((r - l) >> 1);
            if (check(mid, position, m)) {
    
                res = mid;
                l = mid + 1;
            } else {
    
                r = mid - 1;
            }
        }
        return res;
    }

    public boolean check(int x, int[] position, int m) {
    
        int pre = position[0];
        int cnt = 1;
        for (int i = 1; i < position.length; i++) {
    
            if (position[i] - pre >= x) {
    
                pre = position[i];
                cnt++;
            }
        }
        return cnt >= m;
    }
}

Complexity analysis

• Time complexity ：O(nlog(nS)), among n Is the number of baskets ,S Is the upper limit of basket position . Sorting basket positions requires O(nlogn) Time complexity of , Binary search divides the basket position interval , need O(logS) Time complexity of . Whether the statistical answer meets the requirements every time O(n) Time complexity of , So the total time complexity is O(nlogn+nlogS)=O(nlog(nS)).

• Spatial complexity ：O(logn), That is, the stack space required for sorting .