当前位置:网站首页>Summary of game theory
Summary of game theory
2022-07-06 16:25:00 【AC__ dream】
Game theory generally determines the winner or loser by discussing the winning state and losing state , Next, I will introduce some common game theory conclusions through this method .
Bash Game : A pile of items has n individual , Two people take turns taking things from the pile , It is stipulated that at least one , Most take m individual . The last winner wins .
analysis :
If n<m+1, Then the first hand can take all the items at one time , The first step is to win
If n=m+1, Then take several items first , Can ensure that the back hand can take the remaining items at one time , In other words, the first hand will lose .
about n>m+1, There must be n=k *(m+1)+ r
if r!=0, You can finish it for the first time r Items , So for the back hand k Items , The first hand always takes (m+1-k) One item to make the remaining items m+1 Multiple , That is to maintain the inevitable failure state of the backhand , So that the first hand will win .
if r=0, Take it first k Items , The back hand always takes (m+1-k) One item to make the remaining items m+1 Multiple , That is to maintain the state of being the first to lose , So that the hindhand will win .
in general : If n yes m+1 Multiple , Then you will lose first , On the contrary, first hand wins , Here is the judgment code :
#include<cstring>
int main
{
int n,k;
cin>>n>>k;
if(n%(k+1)==0) printf(" The second is the winner ");
else printf(" The first step is to win ");
return 0;
}Fibonacci game : A pile of stones has n individual , Take turns to take , The first mover can go to any number of... For the first time , But you can't take it all , The number of stones taken each time in the future shall not exceed the number taken last time 2 times . The winner is the winner .
Give a conclusion first : The first hand wins if and only if n Not Fibonacci number .
Let's talk about why you're n It's Fibonacci. If you start first, you'll lose :
We prove this by mathematical induction :
set up n=f[i] ( The first i Fibonacci Numbers )
When n=f[3]=2 when , Obviously, the first hand will lose
Suppose you were i<=k There are always forerunners and losers .
Then when i=k+1 when , Yes n=f[k+1]=f[k]+f[k-1]
Let's put this pile n The stones are divided into two piles , The number of stones in a pile is f[k-1] individual , The number of stones in another pile is f[k] individual .
If the number of stones taken for the first time is greater than or equal to f[k-1] individual , because f[k]=f[k-1]+f[k-2]<2*f[k-1], Therefore, the backhand can directly take the remaining stones and win directly .
The main problem we need to consider is that the number of stones finally taken is f[k-1] What was the number of stones taken that time , The number of stones taken last depends on the number of stones taken last time
Let's consider the extreme case first , Is to take it directly for the first time f[k-1]/3 A stone , In this way, the back hand directly takes 2*f[k-1]/3 A stone , In this way, the first pile of stones has been taken away , Let's first see if the number of stones can be put by the back hand at one time is f[k] All the stones have been taken away , That is to say, comparison 4*f[k-1]/3 And f[k] Size , Obviously f[k] Be greater than 4*f[k-1]/3, In other words, in this case, the number of stones can't be... At one time f[k] All the stones have been taken away , This is equivalent to i=k The situation of the , That is, you can't get all the stones at one time , The total number of stones is f[k], If the number of stones taken for the first time is f[k-1]/3~f[k-1] Between , Let's assume that x, Then the back hand can choose to take f[k-1]-x So as to complete the first pile of stones , So the problem turns into i=k The situation of the , Here we have proved that when n It's Fibonacci who will lose first .
Now let's take a look at why n It's not Fibonacci who wins first :
Introduce a theorem here (Zeckendorf Theorem ): Any positive Integers Can be expressed as several discontinuous Fibonacci number ( Excluding the first Fibonacci number ) The sum of the .
such as 96=55+21+13+5+2
therefore n=f[x1]+f[x2]+……+f[xn](x1>x2>……>xn)
For arbitrary i>j+1 There are f[i]>2*f[j], Let's finish the first time f[xn], Then the back hand can't take it all at once f[xn-1], We can ensure that our backers will fall into the inevitable failure state of the current pile of stones ( The number of stones is Fibonacci number ). So we proved the winning strategy of the first hand .
f[0]=f[1]=1;
while(f[i-1]<n)
{
if(f[i-1]+f[i]==n)
return true;
i++;
}
return false;Nimm Game : Yes n Heap items , Take turns to take , Take at least... From a pile at a time 1 individual , The last winner wins .
Let's start with the conclusion : We will first n Stack items for bitwise XOR , If the result after XOR is 0, You will lose first , On the contrary, first hand wins .
The following gives if n The result of stone exclusive or is not 0 The strategy of being the first to win :
Might as well set 10 The result of stone exclusive or is 0111001100, So what should I do first ? The ninth place of the XOR result is 1 It can be seen that there must be a pile of items that meet the number of items. The ninth bit in the binary split is 1, We compare the number of items in this pile with 0111001100 The result of XOR must be less than the original number of this pile of items ( Because the result after XOR is 9 The bit value becomes 0). Let's assume that the value after XOR is 0011010100, Then we can select items from this pile and reduce the number of items in this pile to 0011010100, In this way, the XOR value of the remaining items becomes 0000000000, Do this every time , You can maintain this equilibrium , So as to ensure that the first hand will win .
obviously , When the initial n The exclusive or value of stack items is 0, Then no matter how you choose first, you will break this equilibrium , So that the backhand will enter the winning state .
Code :
#include<cstring>
int main
{
int ans=0,n;
cin>>n;
for(int i=1;i<=n;i++)
{
int t;
scanf("%d",&t);
ans^=t;
}
if(ans) printf(" The first step is to win ");
else printf(" The second is the winner ");
return 0;
}Weizov game : There are two piles of several items each , Two people take turns to remove at least one item from any pile or as many items from both piles , It is stipulated that at least one , At most , The last one who takes the light wins .
Let's first analyze two sets of data :
The first group :(1,2)
If you take one of the first piles first , Then the back hand directly takes the second pile , The backhand wins .
If you take one of the second pile first , Then the back hand takes one of the two piles at the same time , It becomes (0,0), It's also a backhand win
If you take two from the second pile first , Then the back hand directly takes the first pile , Or the backhand wins
Therefore, for this group of data, it is inevitable .
The second group :(3,5)
If you take one of the first piles first , Then take the second pile of 4 individual , therefore (3,5)——>(2,1), Because this is a state of failure , So the backhand wins
If you take the first two , Then take the second pile of 3 individual , therefore (3,5)——>(1,2), Or the backhand wins
If you take the first pile first 3 individual , Then the back hand can directly take the second pile , So the backhand wins
If you take the second pile first 1 individual , The backhand can take from both piles at the same time 2 individual , therefore (3,5)——>(1,2), The backhand wins
If you take the second pile first 2 individual , The backhand can take three from two piles at the same time , therefore (3,5)——>(0,0), The backhand wins
If you take the second pile first 3 individual , The backhand can take from both piles at the same time 1 individual , therefore (3,5)——>(2,1), The backhand wins
If you take the second pile first 4 individual , The backhand can take from the first pile 1 individual , therefore (3,5)——>(2,1), The backhand wins
If you take the second pile first 5 individual , Then the backhand can directly finish the first pile and win .
Therefore, this group of data is also bound to fail .
First list a few groups of relatively small inevitable failure states :
(1,2)
(3,5)
(4,7)
(6,10)
(8,13)
(9,15)
(11,18)
(12,20)
Observe these necessary States , Three conclusions can be found :
(1) The difference between the two adjacent groups increases each time 1, The difference of the first group is 1, The difference of the second group is 2,……, The first n The group difference is n
(2) Every number in the fail state only appears once , And the first value of each mandatory state is the previous mandatory state
The smallest natural number that has never appeared .
(3) The smaller fraction of each inevitable state is their difference 1.618 Round down .( The most important conclusion )
So we can judge whether this state will fail by judging the relationship between the difference between the two numbers and the smaller number between the two numbers
Let's think about such a question , If you give us two numbers m and n, These two numbers do not satisfy the characteristics of the inevitable state , Can we do an operation to make them fail ?
The answer is obvious , But we need to discuss it in two cases :( Hypothetical hypothesis m>n)
set up x by (m-n)*1.618 The value obtained by rounding down
Case one :n>x, Then take... Directly from the two piles at the same time (n-x) One item can make (n,m)——>(x,m-n+x), Obviously, the converted state is a state of failure . Because smaller numbers x The difference between them 1.618 Double up rounding is the same
The second case :n<x:
if n Not in the previous state of failure , explain n It must be the smaller value in a certain failure state , The larger value in the inevitable state is the same as n Of the difference between 1.618 The value obtained by rounding down times is n, because n<x, be m>n+n/1.618, the m Turn into n+n/1.618 Just round down .
if n In the previous state of failure , explain n It must appear as the larger value in the failure state , Therefore, the smaller value in the inevitable failure state must be less than m, Direct will m Change to the smaller value in the failed state to realize the transition to the failed state .
I wrote the detailed proof on a piece of paper , Interested partners can refer to :

Be careful , We don't usually use it directly 1.618, But through (sqrt(5.0) + 1) / 2 obtain .
Here is the core judgment code :
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
int n,m;
cin>>n>>m;
if(n>m) swap(n,m);
double e=(sqrt(5.0)+1)/2;
if(n==(int)((m-n)*e)) printf(" First you lose ");
else printf(" The first step is to win ");
return 0;
} 边栏推荐
- 605. Planting flowers
- Luogu P1102 A-B number pair (dichotomy, map, double pointer)
- 使用jq实现全选 反选 和全不选-冯浩的博客
- AcWing:第56场周赛
- Problem - 922D、Robot Vacuum Cleaner - Codeforces
- Differential (one-dimensional, two-dimensional, three-dimensional) Blue Bridge Cup three body attack
- 指定格式时间,月份天数前补零
- 1323. Maximum number of 6 and 9
- 875. 爱吃香蕉的珂珂 - 力扣(LeetCode)
- Specify the format time, and fill in zero before the month and days
猜你喜欢
D - function (HDU - 6546) girls' competition
本地可视化工具连接阿里云centOS服务器的redis
OneForAll安装使用

pytorch提取骨架(可微)
Quick to typescript Guide
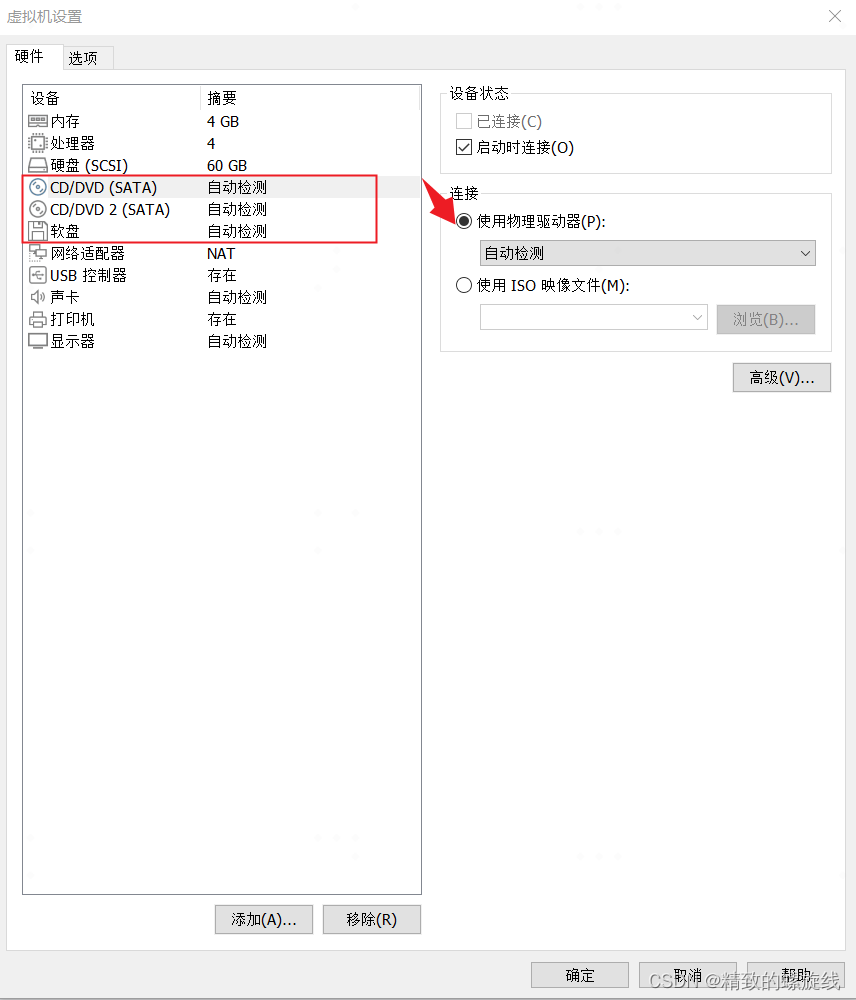
VMware Tools和open-vm-tools的安装与使用:解决虚拟机不全屏和无法传输文件的问题
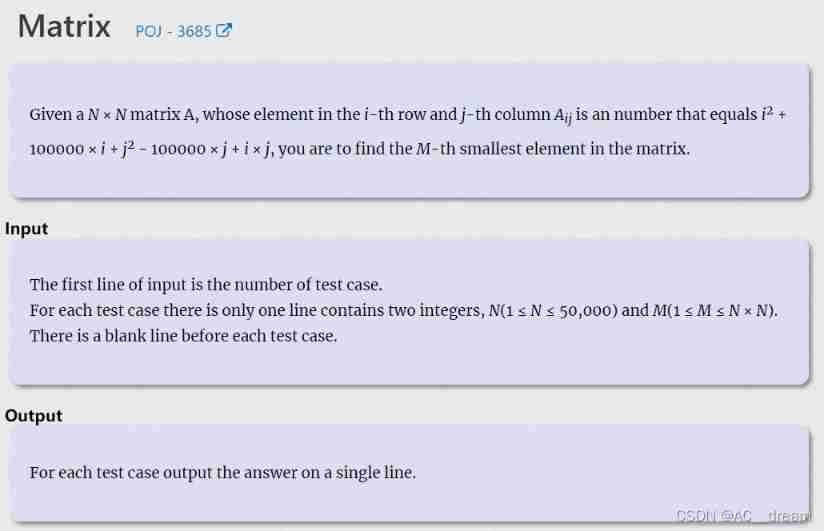
(POJ - 3685) matrix (two sets and two parts)

< li> dot style list style type
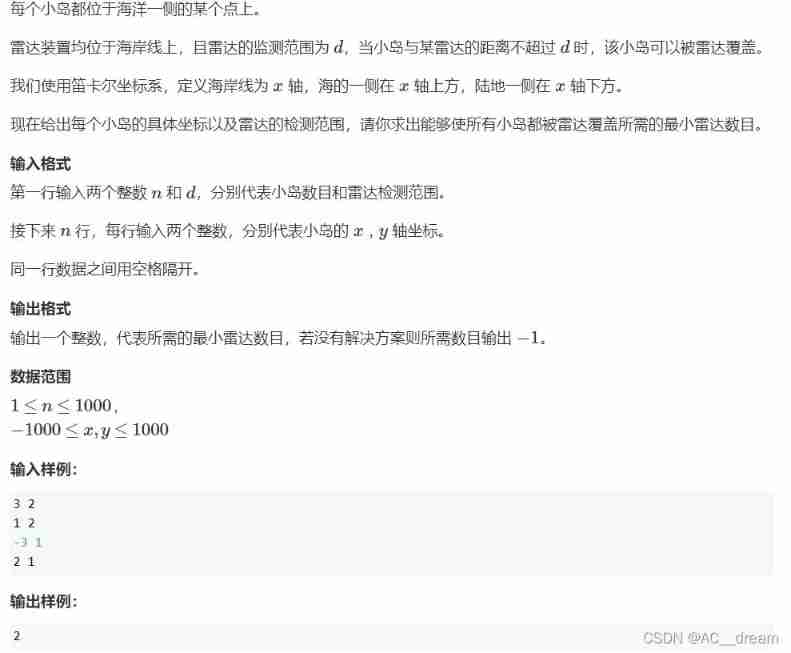
Radar equipment (greedy)
Some problems encountered in installing pytorch in windows11 CONDA
随机推荐
Determine the Photo Position
HDU - 6024 building shops (girls' competition)
Install Jupiter notebook under Anaconda
E. Breaking the Wall
Acwing: Game 58 of the week
第 300 场周赛 - 力扣(LeetCode)
Codeforces Round #801 (Div. 2)A~C
Understand what is a programming language in a popular way
1323. Maximum number of 6 and 9
TCP's three handshakes and four waves
树莓派4B安装opencv3.4.0
QT simulates mouse events and realizes clicking, double clicking, moving and dragging
useEffect,函数组件挂载和卸载时触发
Codeforces Round #800 (Div. 2)AC
Educational Codeforces Round 130 (Rated for Div. 2)A~C
Input can only input numbers, limited input
window11 conda安装pytorch过程中遇到的一些问题
OneForAll安装使用
Raspberry pie 4B installation opencv3.4.0
Problem - 922D、Robot Vacuum Cleaner - Codeforces