当前位置:网站首页>Base dice (dynamic programming + matrix fast power)
Base dice (dynamic programming + matrix fast power)
2022-07-06 16:25:00 【AC__ dream】

My first idea when I see this topic is dynamic programming , set up dp[i][j] It means that we enumerated i Dice with j Number of alternatives , Then it is obviously initialized to dp[1][j]=4(j=1~6)( Different side directions are calculated according to different schemes ), The recursive process is very simple , Namely dp[i][j]=vis[(j+2)%6+1][k]*dp[i-1][k](k=1,2,3,4,5,6),(j+2)%6+1 Representative is j The opposite number of , Analysis I think this topic is finished , Then write the code and run it. The result is also right , Timeout was found after submission , At this time, the data range is 1E9, Linear DP It's impossible to do it , Generally, we need to use the fast power of matrix to optimize , With dp[i][j]=vis[(j+2)%6+1][k]*dp[i-1][k] This recursion , We can get the recursive matrix 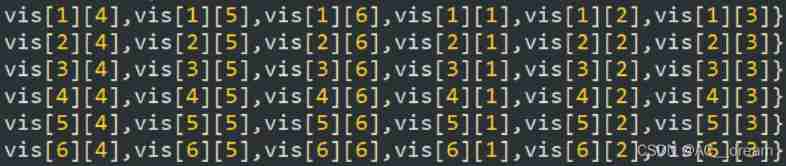
vis[i][j]=0 perhaps 4, if 0 explain i and j Can't be adjacent , Otherwise, it corresponds to four schemes ( The side order is arbitrary ), Initial value of answer matrix f(1,j)=4(j=1,2,3,4,5,6) , Follow this process to solve the matrix fast power
Here is the code :
Code that does not use fast power recursion ( Timeout code ):
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
const int N=1003,mod=1e9+7;
ll dp[N][7];//dp[i][j] By i Dice form the top of j Number of alternatives
int vis[7][7];
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=6;i++)
for(int j=1;j<=6;j++)
vis[i][j]=4;
while(m--)
{
int u,v;
scanf("%d%d",&u,&v);
vis[u][v]=vis[v][u]=0;
}
for(int i=1;i<=6;i++)
dp[1][i]=4;
for(int i=2;i<=n;i++)
{
for(int j=1;j<=6;j++)
for(int k=1;k<=6;k++)
dp[i][(j+2)%6+1]=(dp[i][(j+2)%6+1]+dp[i-1][k]*vis[j][k])%mod;
}
ll ans=0;
for(int i=1;i<=6;i++)
ans+=dp[n][i];
printf("%lld",ans);
return 0;
} The following is the code of matrix fast power recursion (AC Code ):
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int vis[7][7];
void mul(ll ans[][7],ll a[][7],ll b[][7])
{
ll t[7][7]={0};
for(int i=1;i<=6;i++)
for(int j=1;j<=6;j++)
for(int k=1;k<=6;k++)
t[i][j]=(t[i][j]+a[i][k]*b[k][j])%mod;
memcpy(ans,t,sizeof t);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=6;i++)
for(int j=1;j<=6;j++)
vis[i][j]=4;
while(m--)
{
int u,v;
scanf("%d%d",&u,&v);
vis[u][v]=vis[v][u]=0;
}
ll t[7][7]={
{0,0,0,0,0,0,0},
{0,vis[1][4],vis[1][5],vis[1][6],vis[1][1],vis[1][2],vis[1][3]},
{0,vis[2][4],vis[2][5],vis[2][6],vis[2][1],vis[2][2],vis[2][3]},
{0,vis[3][4],vis[3][5],vis[3][6],vis[3][1],vis[3][2],vis[3][3]},
{0,vis[4][4],vis[4][5],vis[4][6],vis[4][1],vis[4][2],vis[4][3]},
{0,vis[5][4],vis[5][5],vis[5][6],vis[5][1],vis[5][2],vis[5][3]},
{0,vis[6][4],vis[6][5],vis[6][6],vis[6][1],vis[6][2],vis[6][3]},
};
ll ans[7][7]={
{0,0,0,0,0,0,0},
{0,1,0,0,0,0,0},
{0,0,1,0,0,0,0},
{0,0,0,1,0,0,0},
{0,0,0,0,1,0,0},
{0,0,0,0,0,1,0},
{0,0,0,0,0,0,1},
};
n--;
while(n)
{
if(n&1) mul(ans,ans,t);
n>>=1;
mul(t,t,t);
}
ll sum=0;
for(int i=1;i<=6;i++)
for(int j=1;j<=6;j++)
sum=(sum+ans[i][j]*4)%mod;
printf("%lld",sum);
return 0;
}边栏推荐
- Advancedinstaller installation package custom action open file
- VMware Tools和open-vm-tools的安装与使用:解决虚拟机不全屏和无法传输文件的问题
- Hdu-6025-prime sequence (girls' competition)
- pytorch提取骨架(可微)
- Codeforces Round #798 (Div. 2)A~D
- Is the sanic asynchronous framework really so strong? Find truth in practice
- Li Kou - 298th weekly match
- 860. Lemonade change
- QT implementation window gradually disappears qpropertyanimation+ progress bar
- 1529. Minimum number of suffix flips
猜你喜欢
2027. Minimum number of operations to convert strings
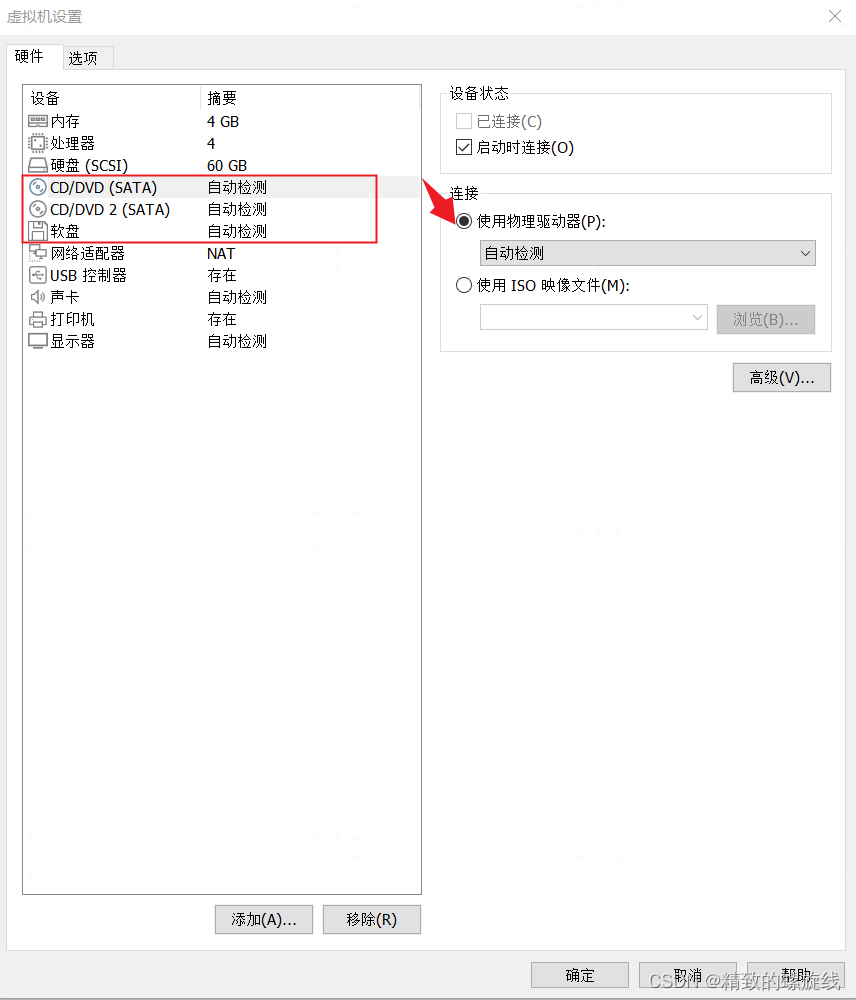
Installation and use of VMware Tools and open VM tools: solve the problems of incomplete screen and unable to transfer files of virtual machines

Remove the border when input is focused

Openwrt build Hello ipk

QT实现窗口渐变消失QPropertyAnimation+进度条
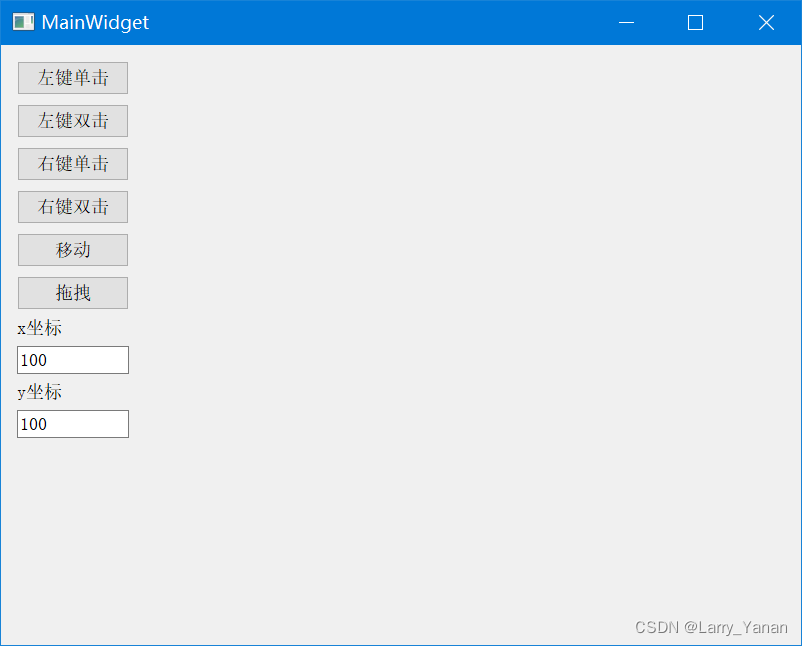
QT模拟鼠标事件,实现点击双击移动拖拽等
分享一个在树莓派运行dash应用的实例。

Basic Q & A of introductory C language
第 300 场周赛 - 力扣(LeetCode)
Codeforces Round #801 (Div. 2)A~C
随机推荐
Advancedinstaller installation package custom action open file
Remove the border when input is focused
Ball Dropping
Effet d'utilisation, déclenché lorsque les composants de la fonction sont montés et déchargés
Luogu P1102 A-B number pair (dichotomy, map, double pointer)
VMware Tools和open-vm-tools的安装与使用:解决虚拟机不全屏和无法传输文件的问题
Radar equipment (greedy)
指定格式时间,月份天数前补零
双向链表—全部操作
Hdu-6025-prime sequence (girls' competition)
What is the difficulty of programming?
Opencv learning log 24 -- Hough transform 2 (maximum interval and minimum length can be limited)
C language is the watershed between low-level and high-level
Date plus 1 day
C basic grammar
Write web games in C language
MariaDB的安装与配置
Opencv learning log 29 -- gamma correction
useEffect,函數組件掛載和卸載時觸發
Maximum product (greedy)