当前位置:网站首页>F - true liars (category and search set +dp)
F - true liars (category and search set +dp)
2022-07-06 06:14:00 【RCyyds】
Portal : True Liars


The question : give n To the relationship ,p1 I'm a good man ,p2 I'm a bad guy . Requirements according to n Find out what good people are in the relationship , If the scheme is unique , Then output good people one by one , The final output end; If the scheme is not unique / Can't find , Then output no
Ideas : It's the first time to encounter this type of problem , After thinking for a long time, I have no idea , Refer to others' blogs Just understand .
The following is the idea of the referenced blog :
Through simple analysis, we can get , For each relationship (x,y,yes/no), If the relationship is yes, be x and y Belong to the same category ; If the relationship is no, be x and y Belong to the opposite class .
According to the preliminary n To the relationship , We can only introduce those who belong to the same category , Which people belong to the opposite category , But it's not sure what kind of good people are / The bad guys . We can define the opposite two kinds of people as a large set , Then there are two small sets in the large set . According to the meaning , We just need from each large set , Choose one of the small sets , Make the total number of people in all the selected small sets be p1 that will do .
Code :
#include <cstdio>
#include <cstring>
#include <iostream>
#define MAXN 600
using namespace std;
int parent[MAXN], path[MAXN][MAXN], dp[MAXN][MAXN];
int num[MAXN]; // Record that the root node of the large set is i Yes, it is num[i] A large collection
int flag[MAXN][2]; // Mark the small set selected to the final result in each large set
int cnt[MAXN][2]; // The root node is i when , Record the number of people contained in the two small sets
int relat[MAXN];
/* relation
* relat=0/1.0 Express i And root nodes parent[i] Related to , That is, it belongs to the same small set ;1 Express i Not associated with root node , That is, different small sets belonging to the same large set */
int find(int x) {
if (x != parent[x]) { // Here parent[x] It's the old father
int px = find(parent[x]); // px It's the new father
relat[x] ^= relat[parent[x]];
/* Due to path compression x The parent node of points directly to the root node , That is, it changes x The father node of , So update the node x Relationship with root node .
*/
parent[x] = px;
}
return parent[x];
}
/*
about "relat[x] ^= relat[parent[x]];" XOR interpretation :
It can be concluded through simple analysis :
1. If ( relation[x And old father ]=0 && relation[ Old father and new father ]=0 ) perhaps (
relation[x And old father ]=1 && relation[ Old father and new father ]=1 ), be relation[x And the new father ]=0
2. If (relation[x And old father ]=1 && relation[ Old father and new father ]=0 ) perhaps (
relation[x And old father ]=0 && relation[ Old father and new father ]=1 ), be relation[x And the new father ]=1
You can find , Final relatino[x And the new father ] = relation[x And old father ] ^ relation[ Old father and new father ]
namely : relat[x] ^= relat[parent[x]];
For the following merge XOR in function is the same
*/
void merge(int x, int y, int d) { // d Either for 0, Either for 1
int px = find(x);
int py = find(y);
if (px != py) {
parent[py] = px;
relat[py] = relat[x] ^ relat[y] ^ d;
}
}
int main(void) {
int m, p, q;
while (scanf("%d%d%d", &m, &p, &q)) {
if (m + p + q == 0) {
break;
}
for (int i = 1; i <= p + q; i++) { //** Initial remarks
relat[i] = 0;
parent[i] = i;
}
while (m--) {
int x, y, d = 1;
char ch[5];
scanf("%d%d%s", &x, &y, ch);
if (ch[0] == 'y') {
d = 0;
}
merge(x, y, d);
}
memset(num, 0, sizeof(num)); //**num Store the number of sets and number them
memset(path, 0, sizeof(path));
memset(cnt, 0, sizeof(cnt));
memset(dp, 0, sizeof(dp));
memset(flag, 0, sizeof(flag));
int tot = 0;
for (int i = 1; i <= p + q; i++) { //** Count the number of sets and number
if (find(i) == i) {
num[i] = ++tot; // tot Number of connected blocks ,num Record root=i The number of the connected block of
}
}
for (int i = 1; i <= p + q;
i++) { //** Count the number of two types of each set and store them in cnt in
cnt[num[find(i)]][relat[i]]++;
}
dp[0][0] = 1;
for (int i = 1; i <= tot; i++) { // tot=2
for (int j = 0; j <= p+q; j++) { // p+q=7
//**dp[i][j] Store to page i Select the kind and for sets j The number of ways
if (j - cnt[i][0] >= 0 && dp[i - 1][j - cnt[i][0]]) {
dp[i][j] += dp[i - 1][j - cnt[i][0]];
path[i][j] =
cnt[i][0]; //**path Array record path , That is 1 still 0
}
if (j - cnt[i][1] >= 0 && dp[i - 1][j - cnt[i][1]]) {
dp[i][j] += dp[i - 1][j - cnt[i][1]];
path[i][j] = cnt[i][1];
}
}
}
/*
There are two in this part if It's a little hard to understand , Because you may think , Two if If you are satisfied , So the final result is dp[i][j] It is possible that two small sets are selected from the same large set , It's against “ Select only one small set from a large set ” The situation of . but , You can find , We finally limited the number of methods to dp[tot][p]=1 when , There is only one plan . If it's like the two just mentioned if All satisfied with , that dp[i][j] A certain >1, It will not meet the following dp[tot][p]=1 Limit , So it solved the problem .
*/
if (dp[tot][p] != 1) {
printf("no\n");
} else {
for (int i = tot, j = p; j > 0 && i > 0; i--) { //** Tag path
if (path[i][j] == cnt[i][0]) {
flag[i][0] = 1;
} else {
flag[i][1] = 1;
}
j -= path[i][j];
// Remember to reduce . Because I just choose enough backpacks p, So follow p Gradually reduce the items at that time , Find the way
}
for (int i = 1; i <= p + q; i++) {
if (flag[num[find(i)]][relat[i]]) {
printf("%d\n", i);
}
}
printf("end\n");
}
}
return 0;
}
边栏推荐
- [C language] string left rotation
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- 数学三大核心领域概述:几何
- 【C语言】qsort函数
- 【无App Push 通用测试方案
- 异常检测方法总结
- 【eolink】PC客户端安装
- Clock in during winter vacation
- 黑猫带你学UFS协议第18篇:UFS如何配置逻辑单元(LU Management)
- 功能安全之故障(fault),错误(error),失效(failure)
猜你喜欢
![Buuctf-[[gwctf 2019] I have a database (xiaoyute detailed explanation)](/img/2c/43ce298794589c5282edda94161d62.jpg)
Buuctf-[[gwctf 2019] I have a database (xiaoyute detailed explanation)
Understanding of processes and threads
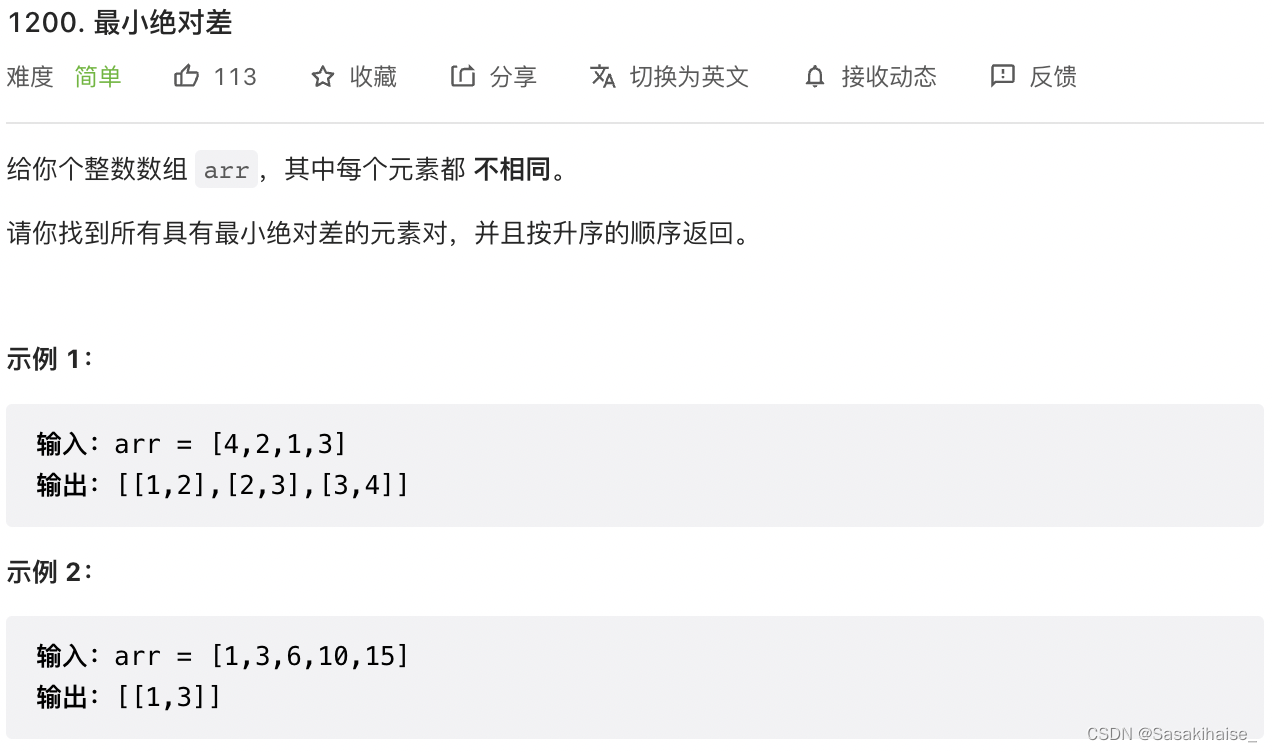
LeetCode 1200. 最小绝对差
SQLMAP使用教程(三)实战技巧二
Clock in during winter vacation

Overview of three core areas of Mathematics: algebra

Digital triangle model acwing 1015 Picking flowers

10m25dcf484c8g (FPGA) amy-6m-0002 BGA GPS module

win10无法操作(删除、剪切)文件
P问题、NP问题、NPC问题、NP-hard问题详解
随机推荐
黑猫带你学eMMC协议第10篇:eMMC读写操作详解(read & write)
isam2运行流程
Network protocol model
Cognitive introspection
公司視頻加速播放
Bit operation rules
【无App Push 通用测试方案
[C language] string left rotation
[postman] dynamic variable (also known as mock function)
Significance of unit testing
曼哈顿距离与曼哈顿矩形-打印回字型矩阵
LeetCode 739. 每日温度
Detailed explanation of BF and KMP
Testing and debugging of multithreaded applications
LeetCode 729. 我的日程安排表 I
Expose the serial fraudster Liu Qing in the currency circle, and default hundreds of millions of Cheng Laolai
Hypothesis testing learning notes
[postman] collections - run the imported data file of the configuration
Configuring OSPF GR features for Huawei devices
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower