当前位置：网站首页>Basic knowledge of error

Basic knowledge of error

2022-07-06 06:04:00 【Zhan Miao】

1. Source of error

Numerical calculation of practical problems with computer , Calculation error is inevitable . There are four main sources of error ：

1.1. Model error

Describe practical problems with mathematical models , Generally, some simplification should be made , There will be differences between the solution of the mathematical model and the solution of the actual problem , This difference is called model error .

1.2. Observation error

Some parameters or constants contained in the mathematical model , It is often obtained by instrument observation or experiment , There will be an error between the observed value and the actual value , This error is called observation error .

1.3. Truncation error

The numerical calculation method used to solve the mathematical model is often the approximate method , Thus, only the approximate solution of the mathematical model can be obtained , The resulting error is called method error . Because the approximate method generally uses the finite four arithmetic operation steps to replace the infinite limit operation , This error caused by truncating an infinite process , Is truncation error . Therefore, the method error is also called truncation error .

1.4. Rounding error

Because the electronic digital computer can only express numbers as finite bits for operation , Therefore, numbers exceeding digits should be rounded according to certain rules , The resulting error is called rounding error .

The numerical calculation method mainly studies the influence of truncation error and rounding error on the calculation results , Generally, model error and observation error are not considered .

2. Absolute error and relative error

The data processed in numerical calculation and the results of calculation , It is usually approximate , There is an error between them and the exact value .

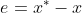set up x^* Is the exact value x An approximation of , said e=x^*-x Is approximate x^* The absolute error of .

Approximate value x^* Absolute error and accuracy of x The ratio is called the approximate value x^* The relative error of , Write it down as

$e_r=\frac{e}{x}=\frac{x^*-x}{x}$

actually , Due to the accurate value x It is unknown. , Therefore, the relative error is usually changed to

$e_r=\frac{e}{x}=\frac{x^*-x}{x^*}$

3. Error estimation and algorithm stability of numerical calculation

The error propagation in numerical calculation is complex , It is difficult to accurately estimate the error of each calculation step , Therefore, the differential error analysis method is usually used to estimate the error , That is, if the error is small, ignore the second-order and higher-order small quantities of error .

The so-called numerical stable algorithm refers to , In the process of digital computer executing this numerical algorithm , The resulting rounding error can be controlled within a certain range , And has little effect on the final result . If the rounding error increases during the calculation , Make the final result differ greatly from the accurate value , Such an algorithm is numerically unstable .

4. Some principles that should be paid attention to in numerical calculation

Use the calculation method with good numerical stability , In order to control the propagation of rounding error ;

When adding and subtracting two numbers with large orders of magnitude , To prevent the small number from adding or subtracting less than the large number ;

Avoid subtracting two similar numbers , In order to avoid serious loss of significant figures ;

In Division , Avoid that the absolute value of the divisor is much smaller than the absolute value of the dividend ;

Prevent machine zero sum overflow shutdown ;

Simplify the calculation steps , Reduce the number of operations .