Working principle of gradient descent algorithm in machine learning

flutter + Applet + Back end ,3 Individuals can open your APP The way | Registration will be sent to Dajiang Yuntai 、 Huawei watch ！>>>

How gradient descent algorithm works in machine learning

author |NIKIL_REDDY compile |VK source |Analytics Vidhya

Introduce

Gradient descent algorithm is one of the most commonly used machine learning algorithms in industry . But it confuses a lot of new people .

If you're new to machine learning , The math behind the gradient decline is not easy . In this paper , My goal is to help you understand the intuition behind the gradient descent .

We will quickly understand the role of the cost function , The explanation for the gradient descent , How to choose learning parameters .

What is the cost function

It's a function , Used to measure the performance of a model against any given data . The cost function quantifies the error between the predicted value and the expected value , And expressed in the form of a single real number .

After assuming the initial parameters , We calculated the cost function . The goal is to reduce the cost function , The gradient descent algorithm is used to modify the given data . Here's the mathematical representation of it ：

_LI.jpg)

What is gradient descent

Suppose you're playing a game , Players are at the top of the mountain , They were asked to reach the lowest point of the mountain . Besides , They're blindfolded . that , How do you think you can get to the lake ？

Before you go on reading , Take a moment to think about .

The best way is to look at the ground , Find out where the ground is falling . From this position , Take a step down , Repeat the process , Until we reach the lowest point .

Gradient descent method is an iterative optimization algorithm for solving local minimum of function .

We need to use the gradient descent method to find the local minimum of the function , The negative gradient of the function at the current point must be selected （ Away from the gradient ） The direction of . If we take a positive direction with the gradient , We are going to approach the local maximum of the function , This process is called gradient rise .

Gradient descent was originally made by Cauchy in 1847 Put forward in . It's also known as steepest descent .

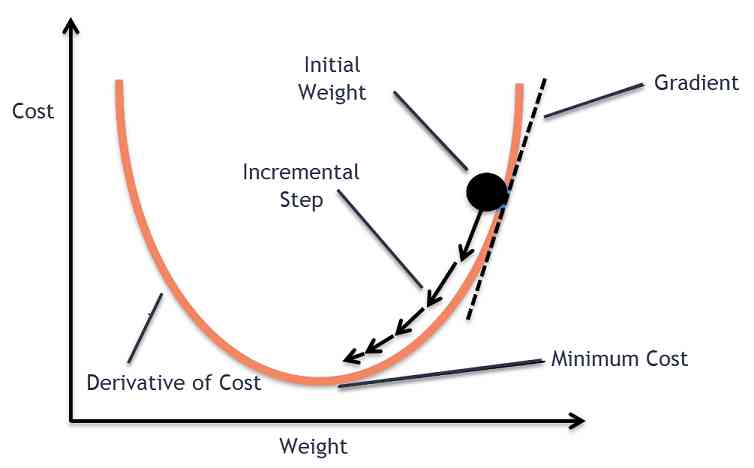
The goal of gradient descent algorithm is to minimize the given function （ For example, the cost function ）. In order to achieve this goal , It iteratively performs two steps ：

1. Calculate the gradient （ Slope ）, The first derivative of a function at that point

2. Do the opposite direction to the gradient （ Move ）

.png)

Alpha It's called the learning rate - An adjustment parameter in the optimization process . It determines the step size .

Draw gradient descent algorithm

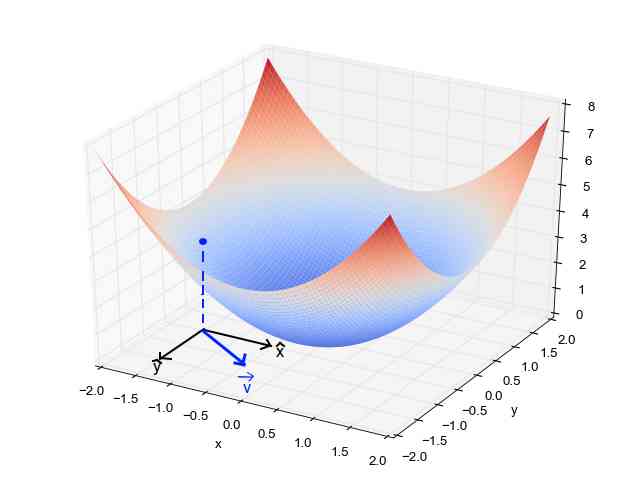
When we have a single parameter （θ）, We can do it in y Plot the dependent variable cost on the axis , stay x Draw on the axis θ. If you have two parameters , We can do three-dimensional drawing , There's a cost on one of the shafts , There are two parameters on the other two axes （θ）.

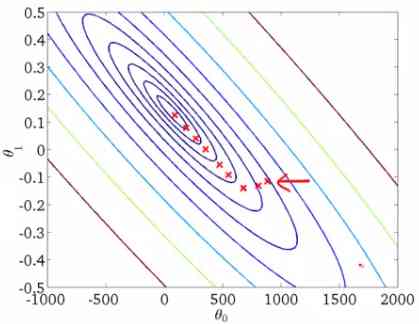
It can also be visualized by using contours . This shows a two-dimensional three-dimensional drawing , These include the parameters along the two axes and the response values of the contour lines . The response value away from the center increases , And it increases with the increase of rings .

α- Learning rate

We have a way forward , Now we have to decide the size of the steps we have to take .

You have to choose carefully , To achieve a local minimum .

• If the learning rate is too high , We may exceed the minimum , It doesn't reach a minimum

• If the learning rate is too low , The training time may be too long

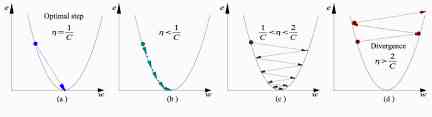
a） The best learning rate , The model converges to the minimum

b） The learning speed is too slow , It takes more time , But it converges to the minimum

c） The learning rate is higher than the optimal value , Slower convergence （1/c<η < 2/c）

d） The learning rate is very high , It will deviate too much from , Deviation from the minimum , Learning performance declines

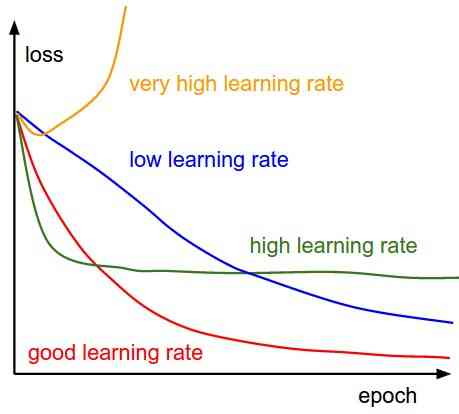
notes ： As the gradient decreases, it moves to the local minimum , Step size reduction . therefore , Learning rate （alpha） It can remain unchanged during the optimization process , And you don't have to change it iteratively .

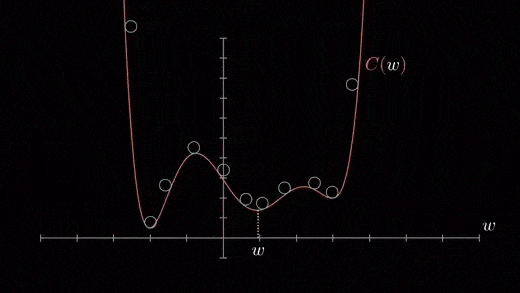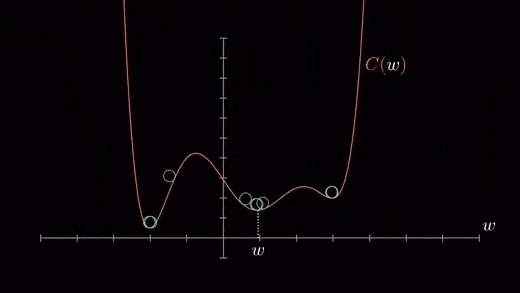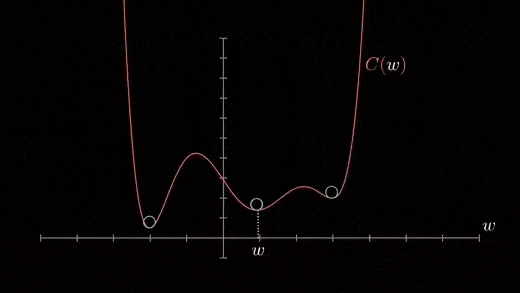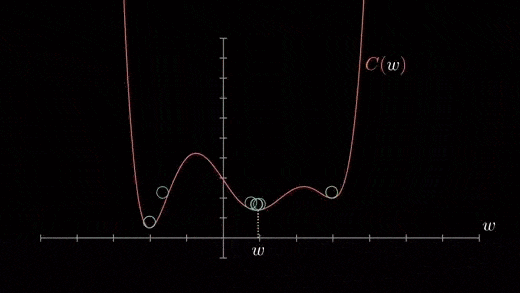
Local minimum

The cost function can consist of many minimum points . The gradient can fall on any minimum , It depends on the starting point （ That's the initial parameter θ） And learning rate . therefore , At different starting points and learning rates , Optimization can converge to different points .

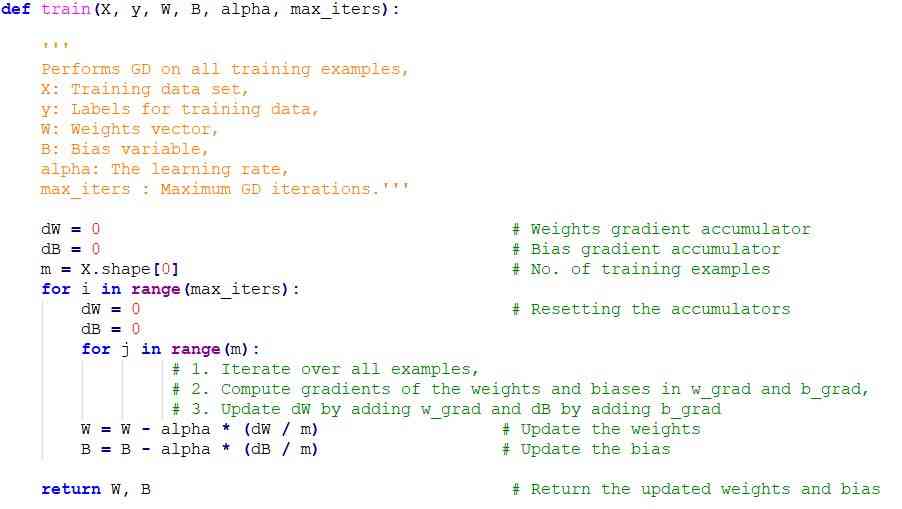
Gradient down Python Code implementation

ending

Once we adjust the learning parameters (alpha) The optimal learning rate is obtained , We start iterating , Until we converge to a local minimum .

Link to the original text ：https://www.analyticsvidhya.com/blog/2020/10/how-does-the-gradient-descent-algorithm-work-in-machine-learning/

Welcome to join us AI Blog station ： http://panchuang.net/

sklearn Machine learning Chinese official documents ： http://sklearn123.com/

Welcome to pay attention to pan Chuang blog resource summary station ： http://docs.panchuang.net/