当前位置:网站首页>French scholars: the explicability of counter attack under optimal transmission theory
French scholars: the explicability of counter attack under optimal transmission theory
2022-07-05 13:26:00 【I love computer vision】
Official account , Find out CV The beauty of Technology
This article shares papers 『When adversarial attacks become interpretable counterfactual explanations』, The explicability of counter attack under optimal transmission theory .
The details are as follows :

The author is from the third University of Toulouse in France and IRT Saint-Exupéry Research institute, .
Thesis link :https://arxiv.org/pdf/2206.06854.pdf
01
introduction
This paper is a theoretical article on countering attacks , The author provides a very reliable explanation for countering attacks . At present, the optimal transmission theory is a very popular direction in the deep learning theory , The author analyzes the phenomenon of anti attack from the perspective of optimal transmission theory . When learning a neural network with dual loss of optimal transmission problem , The gradient of the model is the direction of the optimal transmission scheme , It is also the direction closest to the confrontation sample .
Moving along the gradient to the decision boundary is no longer a counter attack , It's a counterfactual explanation , That is, it can be seen as explicitly transferring from one class to another . Through a large number of experiments on interpretable metrics, we can find , The simple saliency mapping method applied to the optimal transmission network is a reliable explanation , And it is superior to the latest interpretation method in the unconstrained model .
02
Optimal transmission , Robustness and interpretability
Let is about the optimal transmission scheme of minimizing the loss function . Given , Ling is about images . Because it is uncertain , Can be made as the biggest point about , Then there is the following proposition :
( Transmission scheme direction ) Let be an optimal solution to minimize the loss function . Given sum , So when , There are almost everywhere .
This proposition without regularization is true for dual problems . It proves that for most , Indicates the direction of the transmission scheme .
( Decision boundaries ) Let sum be two separable distributions with minimum distance , To minimize an optimal solution of the loss function , among . Given sum , Then there is and , Among them is the decision boundary .
Let sum be two separable distributions with minimum distance , To minimize an optimal solution of the loss function , among , Given , Then there are
Almost everywhere , among .
inference 1 indicate , The classifier based on the loss function can accurately obtain the countermeasure samples . under these circumstances , The best counter attack is in the gradient direction , All attacks applied to the optimal transmission neural network model , Such as attack or attack , Are equivalent to attacks .
To illustrate these propositions , The author learned a dense binary classifier with loss function to separate two complex distributions . The figure below (a) Two distributions are shown ( Blue and orange snowflakes ), The boundaries of learning ( Red dotted line ). The figure below (b) and (c) Shows the random samples in both distributions , Which is defined in proposition 2 Middle paragraph .
Just like the proposition 2 As described , This point falls right on the decision boundary . Besides , Such as proposition 1 Described , Each segment provides the orientation of the image relative to the transportation scheme .
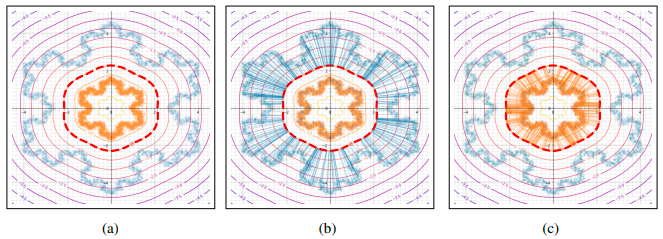
The author proves that the optimal transmission neural network , Counter attacks are known in form , And easy to calculate . Besides , The author also proves that the counter attack is carried out along the transmission map , So fighting attacks is no longer an imperceptible modification , But an understandable transformation of the sample . The author will use these attributes to provide a natural counterfactual explanation , It has provable explanatory properties .
The counterfactual interpretation of the sample in a given class is the closest sample . Because the global information of and is usually not directly available , Therefore, the author only aims at the classifier to obtain its local information . under these circumstances , Counterfactual corresponds to proposition 2 Counter attack defined in . For classical neural networks , This can only be achieved by adding anti noise , This is not a valuable explanation . Because it only depends on and , The definition of this counterfactual interpretation is partial . contrary , The transmission scheme as the minimum of describes the optimal scheme from class to , So the transmission scheme is a global counterfactual explanation , And it is a partial explanation of .
It should be noted that , The transport scheme does not provide the closest sample on the opposite class , But it provides the closest average in the pairing process . According to the proposition 1, The image in the optimal transmission scheme is . Even if only partially known , at that time , It can be seen that on the boundary of decision , And the path of the optimal transmission scheme can be further determined .
In the past, saliency graph only provides a very intuitive and fuzzy explanation for classifier classification , In this paper , The author puts forward a very reliable explanation in the optimal transmission neural network . Indicates the direction of the optimal transmission scheme , Therefore, the saliency diagram shows the importance of each input feature in this direction .
03
hKR Loss function
You know, one disadvantage of functions is , It strongly depends on the parameters of the loss function . In the case of two categories , There are two parameters : Gap parameters and weight parameters respectively , It is used to balance the robustness and accuracy of the classification model . When classes are separable and small enough , The part of the loss function tends to . This makes it difficult to choose parameters , In this paper, the author proposes a new loss formula as follows :
402 Payment Required
Here is a learnable parameter , Is a new parameter . The gap at the boundary is uniformly distributed , When the ratio is , bring , Then the optimal clearance parameters can be obtained , The latter can be explained as the proportion of target data involved in the key part of the loss .
choice , In the process of optimization , The weight part of is roughly the same as the part . Using this method , The only parameter that can be selected is , It can be explained as the approximate error rate of the goal in the learning process . Given a multi classification problem with classes , Is a one to many two classifier , The loss function is as follows
among
402 Payment Required
The above formula has three main shortcomings : One is that the best margins for each class may be different , As a result, a large number of super parameters need to be adjusted ; The second is that the unbalanced distribution of samples in a large number of classes may lead to slow convergence of the model ; The third is ( Functions of real classes ) The weight relative to other categories decreases as the number of categories increases . To overcome these shortcomings , The author proposes a method based on Of Regularization loss function :among , For real categories , And other functions always have the same weight . In the early stages of learning , Because the value of is average ; During the training , The value of will vary gradually , Until a component reaches its maximum and stabilizes .
04
experimental result
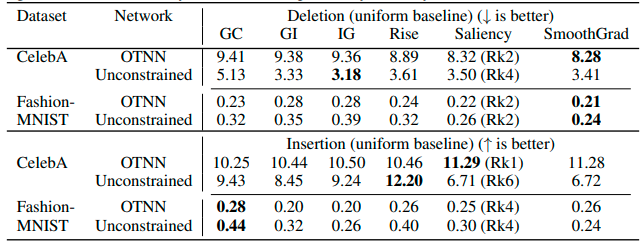
The authors use insertion and deletion indexes to evaluate the quality of saliency map interpretation of optimal transmission neural networks . Classical interpretation methods are evaluated for two types of networks on and datasets .
The following table shows that the saliency map method becomes competitive in the indicators on the optimal transmission neural network and provides a more reliable explanation .
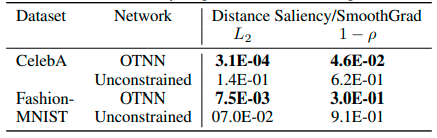
The following table evaluates two indicators and grade correlation coefficients of different data sets on the optimal transmission network . The interpretation distance on the optimal transmission network is much lower than the unconstrained interpretation distance , And very close to .
The following figure shows the qualitative visualization results , The intuitive discovery shows that the optimal neural network provides a better and clearer explanation .

From the quantitative results in the table below, we can find , Through all these experiments, it is concluded that , Use multiple types of interpretive indicators , The interpretability of the optimal transmission neural network is better than that of the unconstrained neural network .
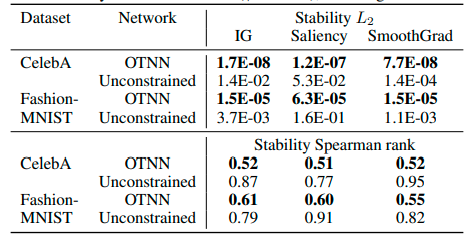
The following two figures show the optimal transmission network learned on and data sets respectively , The following two figures show the original image , The average gradient on the channel , And images with transmission scheme direction . You can intuitively find , Most gradients are visually consistent .



END
Welcome to join 「 Against learning 」 Exchange group notes :Ad

边栏推荐
- mysql econnreset_ Nodejs socket error handling error: read econnreset
- 【Hot100】33. 搜索旋转排序数组
- FPGA 学习笔记:Vivado 2019.1 添加 IP MicroBlaze
- 私有地址有那些
- Flutter 3.0更新后如何应用到小程序开发中
- #从源头解决# 自定义头文件在VS上出现“无法打开源文件“XX.h“的问题
- CAN和CAN FD
- Sorry, we can't open xxxxx Docx, because there is a problem with the content (repackaging problem)
- 49. 字母异位词分组:给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
- Win10 - lightweight gadget
猜你喜欢
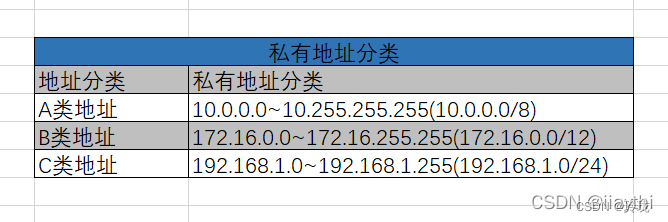
私有地址有那些
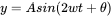
Flutter draws animation effects of wave movement, curves and line graphs

Sorry, we can't open xxxxx Docx, because there is a problem with the content (repackaging problem)
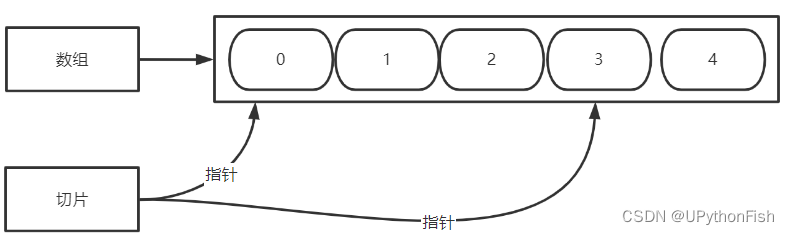
go 数组与切片
What is a network port
Principle and configuration of RSTP protocol

DataPipeline双料入选中国信通院2022数智化图谱、数据库发展报告

MySQL --- 数据库查询 - 排序查询、分页查询
数据湖(七):Iceberg概念及回顾什么是数据湖

LB10S-ASEMI整流桥LB10S
随机推荐
真正的缓存之王,Google Guava 只是弟弟
Get you started with Apache pseudo static configuration
uni-app开发语音识别app,讲究的就是简单快速。
Jenkins installation
一网打尽异步神器CompletableFuture
一文详解ASCII码,Unicode与utf-8
Can and can FD
Put functions in modules
Although the volume and price fall, why are the structural deposits of commercial banks favored by listed companies?
Datapipeline was selected into the 2022 digital intelligence atlas and database development report of China Academy of communications and communications
记录一下在深度学习-一些bug处理
RHCSA9
Alibaba cloud SLB load balancing product basic concept and purchase process
运筹说 第68期|2022年最新影响因子正式发布 快看管科领域期刊的变化
A detailed explanation of ASCII code, Unicode and UTF-8
DataPipeline双料入选中国信通院2022数智化图谱、数据库发展报告
解决uni-app配置页面、tabBar无效问题
Notion 类笔记软件如何选择?Notion 、FlowUs 、Wolai 对比评测
jenkins安装
华为推送服务内容,阅读笔记