当前位置:网站首页>Gradient understanding decline
Gradient understanding decline
2020-11-06 01:14:00 【Artificial intelligence meets pioneer】
author |PHANI8 compile |VK source |Analytics Vidhya
Introduce
In this article , We'll see what a real gradient descent is , Why it became popular , Why? AI and ML Most of the algorithms in follow this technique .
Before we start , What the gradient actually means ? That sounds strange, right !
Cauchy is 1847 The first person to propose gradient descent in
Um. , The word gradient means the increase and decrease of a property ! And falling means moving down . therefore , in general , The act of descending to a certain point and observing and continuing to descend is called gradient descent

therefore , Under normal circumstances , As shown in the figure , The slope of the top of the mountain is very high , Through constant movement , When you get to the foot of the mountain, the slope is the smallest , Or close to or equal to zero . The same applies mathematically .
Let's see how to do it
Gradient descent math
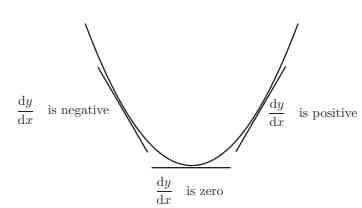
therefore , If you see the shape here is the same as the mountains here . Let's assume that this is a form of y=f(x) The curve of .
Here we know , The slope at any point is y Yes x The derivative of , If you use a curve to check , You'll find that , When you move down , The slope decreases at the tip or minimum and equals zero , When we move up again , The slope will increase
Remember that , We're going to look at the smallest point x and y What happens to the value of ,
Look at the picture below , We have five points in different positions !
.png)
When we move down , We will find that y The value will decrease , So in all the points here , We get a relatively minimum value at the bottom of the graph . therefore , Our conclusion is that we always find the minimum at the bottom of the graph (x,y). Now let's take a look at how ML and DL Pass this , And how to reach the minimum point without traversing the whole graph ?
In any algorithm , Our main purpose is to minimize the loss , This shows that our model works well . To analyze this , We're going to use linear regression
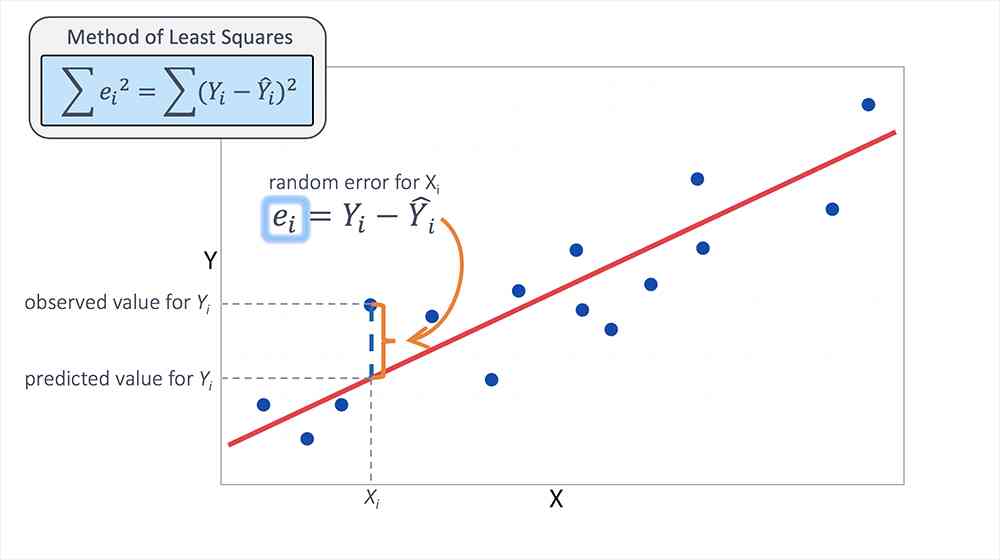
Because linear regression uses straight lines to predict continuous output -
Let's set a straight line y=w*x+c
Here we need to find w and c, In this way, we have the best fitting line to minimize the error . So our goal is to find the best w and c value
Let's start with some random values w and c, We update these values based on the loss , in other words , We update these weights , Until the slope is equal to or close to zero .
We will take y The loss function on the axis ,x There's... On the shaft w and c. Look at the picture below -
.png)
In order to achieve the minimum in the first graph w value , Please follow these steps -
-
use w and c Start calculating a given set of x _values The loss of .
-
Draw points , Now update the weight to -
w_new =w_old – learning_rate * slope at (w_old,loss)
Repeat these steps , Until the minimum value is reached !
-
We subtract the gradient here , Because we want to move to the foot of the mountain , Or moving in the steepest direction of descent
-
When we subtract , We're going to get a smaller slope than the previous one , This is where we want to move to a point where the slope is equal to or close to zero
-
We'll talk about the learning rate later
The same applies to pictures 2, Loss and c Function of
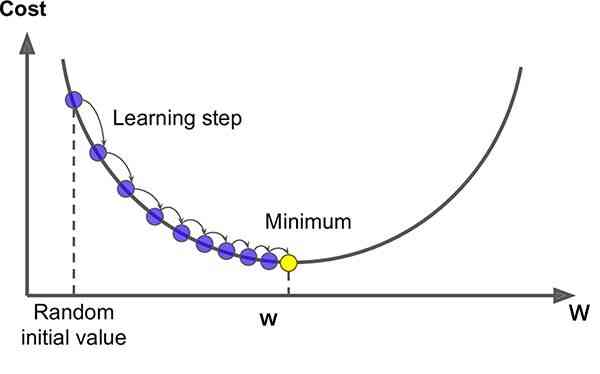
Now the question is why we put learning rate in the equation ? Because we can't traverse all the points between the starting point and the minimum
We need to skip a few points
-
We can take big steps at the beginning .
-
however , When we're close to the minimum , We need to take small steps , Because we're going to cross the minimum , Move to a slope to add . In order to control the step size and movement of the graph , The introduction of learning rate . Even if there is no learning rate , We'll also get the minimum , But what we care about is that our algorithms are faster !!
.png)
Here is an example algorithm for linear regression using gradient descent . Here we use the mean square error as the loss function -
1. Initialize model parameters with zero
m=0,c=0
2. Use (0,1) Any value in the range initializes the learning rate
lr=0.01
The error equation -
.png)
Now use (w*x+c) Instead of Ypred And calculate the partial derivative
.png)
3.c It can also be calculated that
.png)
4. Apply this to all epoch Data set of
for i in range(epochs):
y_pred = w * x +c
D_M = (-2/n) * sum(x * (y_original - y_pred))
D_C = (-2/n) * sum(y_original - y_pred)
Here the summation function adds the gradients of all points at once !
Update parameters for all iterations
W = W – lr * D_M
C = C – lr * D_C
Gradient descent method is used for deep learning of neural networks …
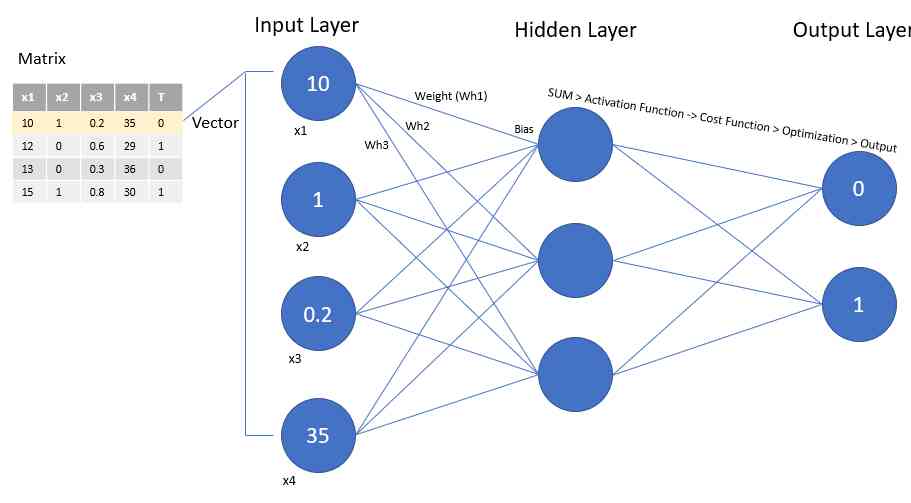
ad locum , We update the weights of each neuron , In order to get the best classification with minimum error . We use gradient descent to update the ownership value of each layer …
Wi = Wi – learning_rate * derivative (Loss function w.r.t Wi)
Why it's popular ?
Gradient descent is the most commonly used optimization strategy in machine learning and deep learning .
It's used to train data models , It can be combined with various algorithms , Easy to understand and implement
Many statistical techniques and methods use GD To minimize and optimize their process .
Reference
- https://en.wikipedia.org/wiki/Gradient_descent
- https://en.wikipedia.org/wiki/Stochastic_gradient_descent
Link to the original text :https://www.analyticsvidhya.com/blog/2020/10/what-does-gradient-descent-actually-mean/
Welcome to join us AI Blog station : http://panchuang.net/
sklearn Machine learning Chinese official documents : http://sklearn123.com/
Welcome to pay attention to pan Chuang blog resource summary station : http://docs.panchuang.net/
版权声明
本文为[Artificial intelligence meets pioneer]所创,转载请带上原文链接,感谢
边栏推荐
猜你喜欢
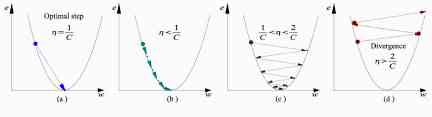
Working principle of gradient descent algorithm in machine learning
Pycharm快捷键 自定义功能形式
JetCache埋点的骚操作,不服不行啊

简直骚操作,ThreadLocal还能当缓存用

How to demote a domain controller in Windows Server 2012 and later

用Python构建和可视化决策树

ipfs正舵者Filecoin落地正当时 FIL币价格破千来了

“颜值经济”的野望:华熙生物净利率六连降,收购案遭上交所问询
网络安全工程师演示:原来***是这样获取你的计算机管理员权限的!【维持】

Didi elasticsearch cluster cross version upgrade and platform reconfiguration
随机推荐
容联完成1.25亿美元F轮融资
DevOps是什么
熬夜总结了报表自动化、数据可视化和挖掘的要点,和你想的不一样
“颜值经济”的野望:华熙生物净利率六连降,收购案遭上交所问询
嘘!异步事件这样用真的好么?
6.7 theme resolver theme style parser (in-depth analysis of SSM and project practice)
Jmeter——ForEach Controller&Loop Controller
DTU连接经常遇到的问题有哪些
7.2.1 cache configuration of static resources
X Window System介紹
Ubuntu18.04上安裝NS-3
基於MVC的RESTFul風格API實戰
drf JWT認證模組與自定製
mac 下常用快捷键,mac启动ftp
Analysis of ThreadLocal principle
自然语言处理之命名实体识别-tanfordcorenlp-NER(一)
数字城市响应相关国家政策大力发展数字孪生平台的建设
条码生成软件如何隐藏部分条码文字
The practice of the architecture of Internet public opinion system
采购供应商系统是什么?采购供应商管理平台解决方案