当前位置:网站首页>C language (high-level) data storage + Practice
C language (high-level) data storage + Practice
2022-07-07 07:20:00 【ℳ white ℳ night ℳ】
Deep analysis of data storage in memory
Introduction
How data type variables are stored in memory ? What is the positive and negative complement ?
This chapter will explain the storage of data in detail .
This chapter uses 32 Bit platform
1. Data type introduction
We've already learned about basic built-in types :
char // Character data type
short // Short
int // plastic
long // Long integer
long long // Longer plastic surgery
float // Single-precision floating-point
double // Double precision floating point
//C Does the language have string type ?
And the amount of storage they occupy .
The meaning of type :
- Use this type to exploit the size of memory space ( Size determines the range of use ).
- How to look at the perspective of memory space .
1.1 Basic classification of types
Plastic surgery Family :
char // because char Type stores ASCII Code value , So it belongs to the plastic surgery family
unsigned char
signed char
short
unsigned short [int]
signed short [int]
int
unsigned int
signed int
long
unsigned long [int]
signed long [int]
Floating point family :
float
double
Construction type :
An array type
Type of structure struct
Enumeration type enum
Joint type union
Pointer types :
int*pi;
char* pc;
float* pf;
void* pv;
Empty type :
void Indicates empty type ( No type )
Usually applied to the return type of a function 、 The parameters of the function 、 Pointer types .
2. Shaping storage in memory
As we mentioned before, the creation of a variable is to open up space in memory . The size of space is determined according to different types .
How data is stored in the opened memory ?
such as :
int a = 20;
int b = -10;
We know for a Allocate four bytes of space .
How to store ?
Come down to understand the following concepts :
2.1 Original code 、 Inverse code 、 Complement code
There are three kinds of integers in the computer 2 Decimal representation , The original code 、 Inverse and complement .
There are three ways of expression Sign bit and Value bits Two parts , The sign bits are all used 0 Express “ just ”, use 1 Express “ negative ”, And the number bit .
A positive number 、 back 、 The complement is the same .
The three representations of negative integers are different .
Original code
The original code can be obtained by directly translating the numerical value into binary in the form of positive and negative numbers .
Inverse code
Change the sign bit of the original code , The reverse code can be obtained by inverting other bits in turn .
Complement code // Values stored in memory
Inverse code +1 You get the complement .
For plastic surgery : Data stored in memory is actually stored in the complement .
Why? ?
In computer system , All values are represented and stored by complements . The reason lies in , Use complement , Symbol bits and value fields can be treated in a unified way ;
meanwhile , Addition and subtraction can also be handled in a unified way (CPU Only adders ) Besides , Complement code and original code are converted to each other , Its operation process is the same , No need for additional hardware circuits .
Let's take an example :
int a=1;
int c=a-1;
It says ,CPU Can only handle addition , in other words c=a+(-1), Let's look at it from a binary point of view .
a The original code is
00000000000000000000000000000001 // The original and inverse complements of positive numbers are the same
-1 The original code is
10000000000000000000000000000001 // Original code
11111111111111111111111111111110 // Inverse code
11111111111111111111111111111111 // Complement code
If according to CPU Methods ,a The original code and -1 The original code of is added and found :
10000000000000000000000000000010
But if there is a complement , give the result as follows :
Let's look at the storage in memory :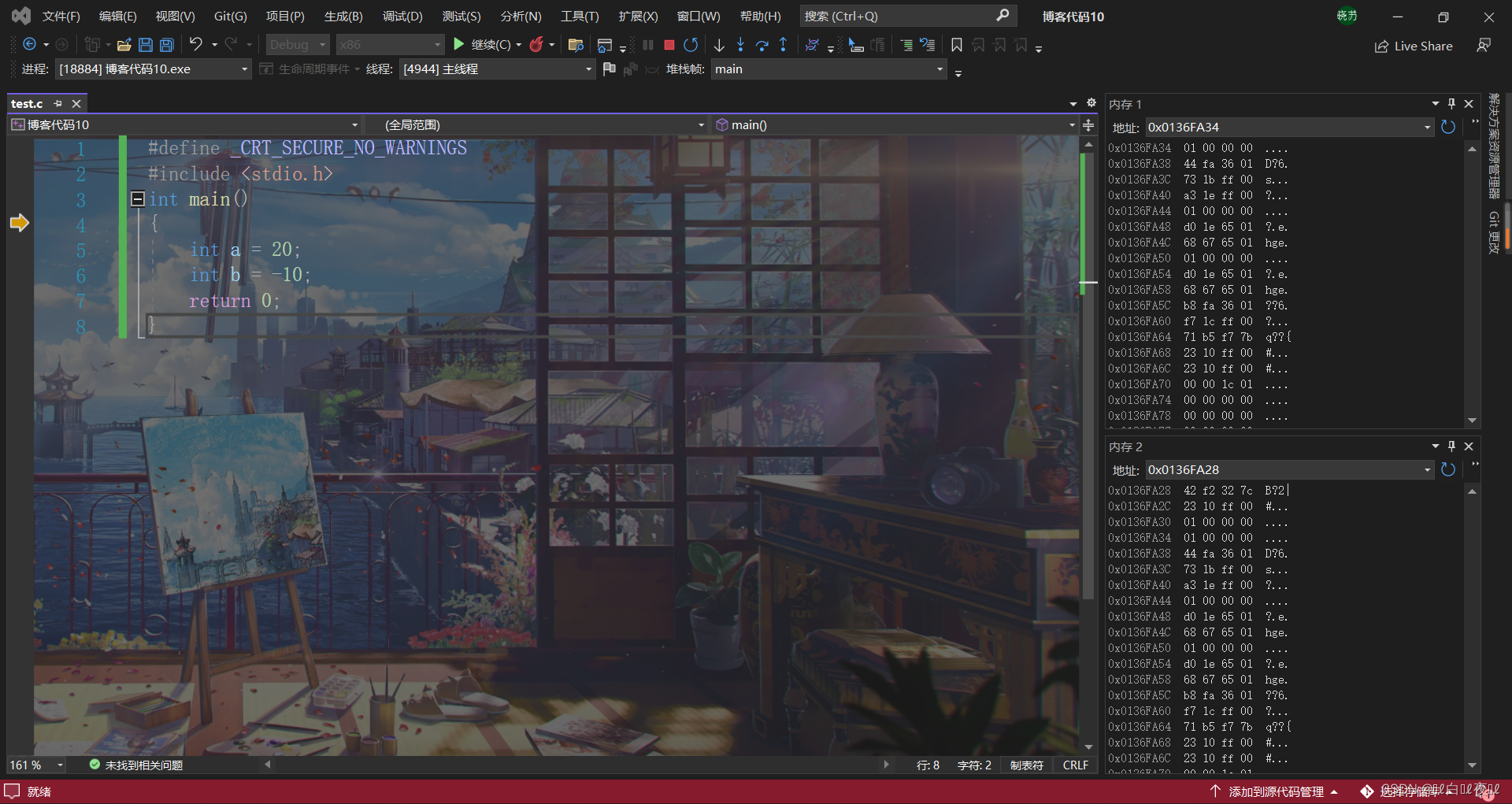
We can see that for a and b The complement code is stored separately . But we found the order a little Something's wrong .
That's why ?
2.2 Introduction to big and small end
What is big end, small end :
Big end ( Storage ) Pattern , The low bit of data is stored in the high address of memory , And the high end of the data , Stored in a low address in memory ;
The small end ( Storage ) Pattern , The low bit of data is stored in the low address of memory , And the high end of the data ,, Stored in a high address in memory .
The value stored in memory is expressed in hexadecimal , As for why not use binary representation , Because binary is too long , And it's not good , But what is actually stored in memory is binary .
We use it 0x11223344 For example :
11 Is the high order of the data ,44 Is the low order of the data 
Why there are big end and small end :
Why are there big and small end patterns ? This is because in a computer system , We are in bytes , Each address corresponds to a byte , A byte is 8 bit. But in C In language, except 8 bit Of char outside , also 16 bit Of short type ,32 bit Of long type ( It depends on the compiler ), in addition , For digits greater than 8 Bit processor , for example 16 Bits or 32 Bit processor , Because the register width is larger than one byte , So there must be a problem of how to arrange multiple bytes . So it leads to big end storage mode and small end storage mode .
for example : One 16bit Of short type x , The address in memory is 0x0010 , x The value of is 0x1122 , that 0x11 For high byte , 0x22 Is low byte . For big end mode , will 0x11 Put it in the low address , namely 0x0010 in , 0x22 Put it in a high address , namely 0x0011 in . The small end model , Just the opposite . That we use a lot X86 The structure is small end mode , and KEIL C51 It's the big end mode . A great deal of ARM,DSP It's all small end mode . There are some ARM The processor can also choose the big end mode or the small end mode by the hardware .
Baidu 2015 System Engineer written test questions :
Please briefly describe the concepts of big end byte order and small end byte order , Design a small program to determine the current machine byte order .
First consider the logic that this code should implement :
We can create a variable as 1, Then take the address , Cast type to char type , Because the address taken is the address of the first byte , So the value in the first byte we print out is 1 still 0.
Reference code :
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char*)&i);
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf(" The small end \n");
}
else
{
printf(" Big end \n");
}
return 0;
}
The result of the code is :
The hardware of my computer is small end storage .
practice
The following code , Without simple thinking , The output will surprise you .
What does the following program output ?
// Code 1
#include <stdio.h>
int main()
{
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a=%d,b=%d,c=%d", a, b, c);
return 0;
}
The code runs as follows :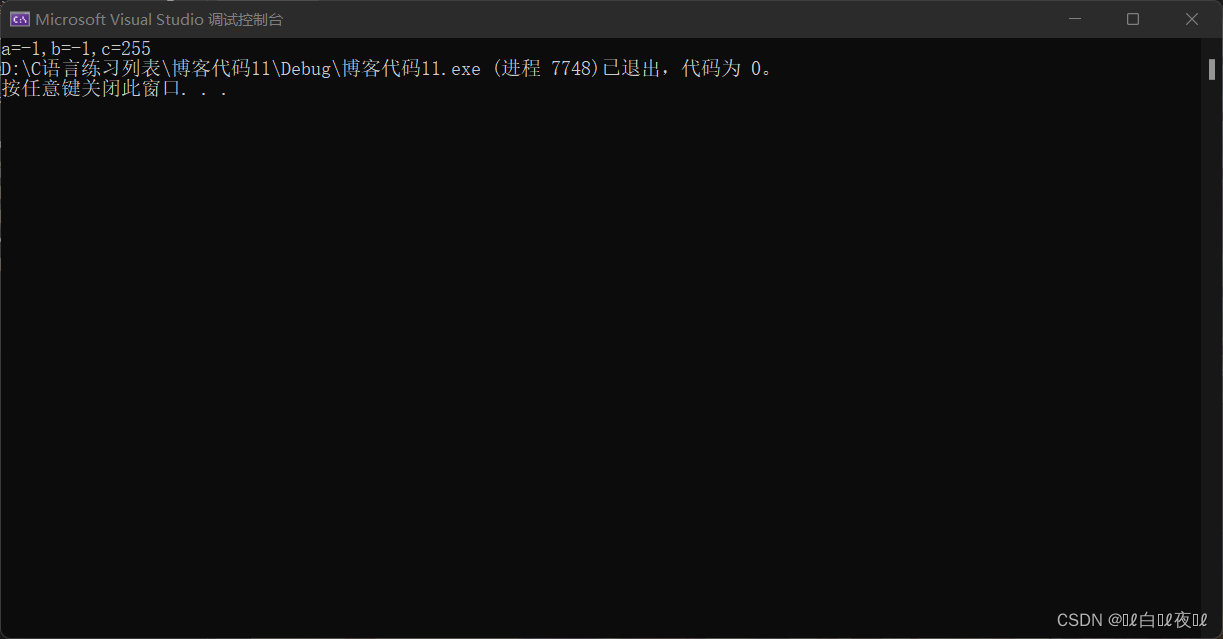
-1 The complement of is
11111111111111111111111111111111
Store into a in , the reason being that char type , So here we will truncation , That is to say, take the last eight bits of binary .
Store into b in , the reason being that signed char( The signed char type ), And the above char Same type .
Store into c in , the reason being that unsigned char( Unsigned char type ), That is to say, there is no sign bit .
We use it when printing %d, Need shaping and lifting ,a and b It's a signed type , So the integer lift is the left fill 1, Last sum -1 The complement of is the same .
However c It's an unsigned type , Left complement 0, The complement after completion is like this :
00000000000000000000000011111111
So what you print out is 255.
// Code 2
#include <stdio.h>
int main()
{
char a = -128;
printf("%u\n", a);
return 0;
}
The code runs as follows :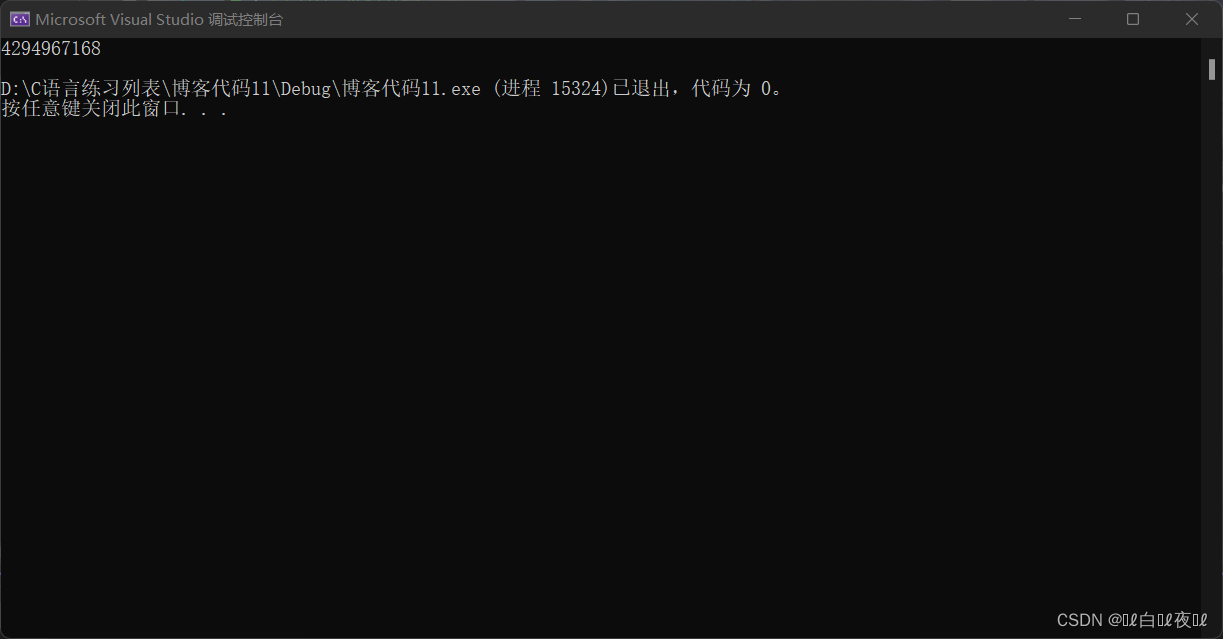
-128 The complement of is :
11111111111111111111111110000000
Store into char Type of a To be truncated in ,10000000, This is a signed bit , What we print is unsigned shaping , So we need to improve integer , It's like this .
11111111111111111111111110000000
Because it is an unsigned integer , The complement is equal to the original code , The result is the big number above .
// Code 3
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n", a);
return 0;
}
The result of this code is the same as above , It's just 128 The complement of is
00000000000000000000000010000000.
// Code 4
#include <stdio.h>
int main()
{
int i = -20;
unsigned int j = 10;
printf("%d\n", i + j);
// Operate in the form of complement , Finally, it is formatted as a signed integer
return 0;
}
Code run results :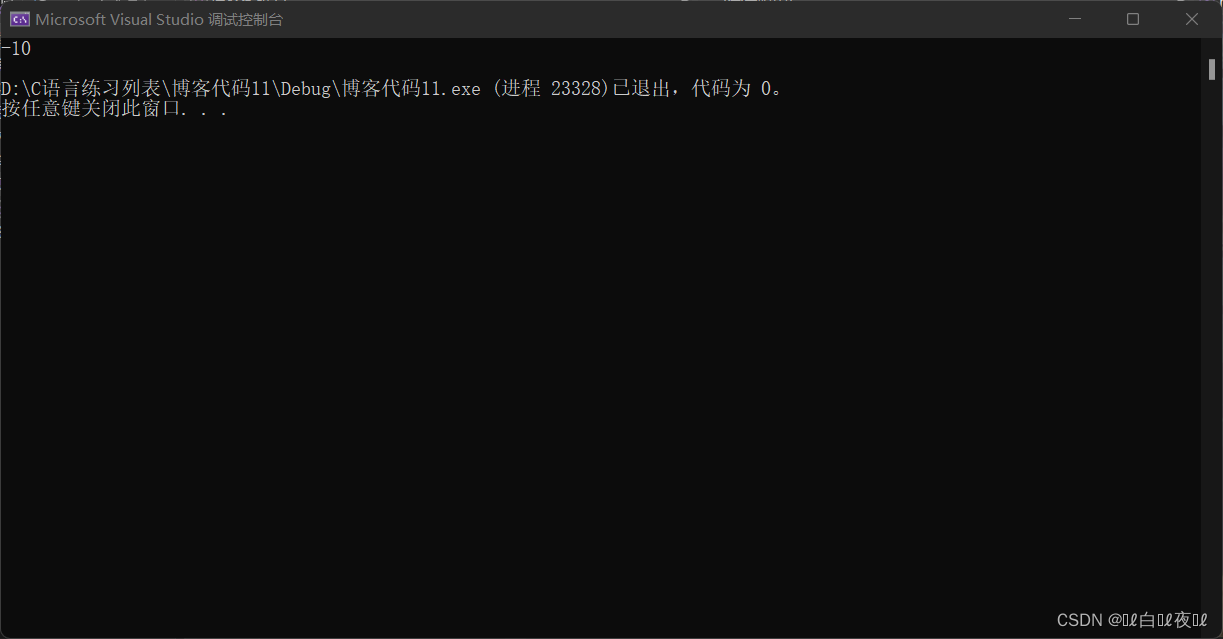
Variable i The complement of is :
11111111111111111111111111101100
Variable j The complement of is :
00000000000000000000000000001010
i+j The complement of is :
i+j The complement of becomes the original code
10000000000000000000000000001010
Finally %d Way to print .
// Code 5
#include <stdio.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}
The printed result of this code is an endless loop .
because i yes unsigned int type , In any case, it is a positive number , So there will be a dead cycle .
// Code 6
#include <stdio.h>
#include <string.h>
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}
The output of this code is :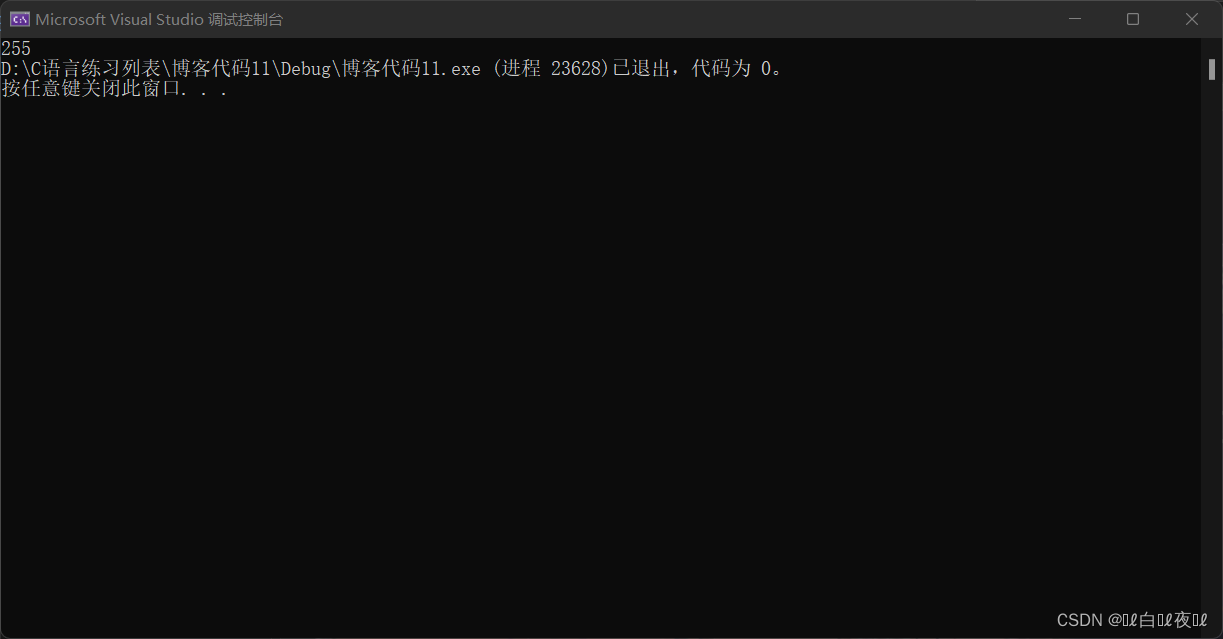
When we first entered the cycle ,char a[1000] The first element in this array is :
-1, And then there was -2…
From a binary point of view :
-1 Complement 11111111111111111111111111111111
-2 Complement 11111111111111111111111111111110
…
We can only store data in the last eight digits , Pay attention here ,strlen It's meeting \0 Then stop , Don't count \0 The location of ,‘\0’ be equal to char Stored inside 0.
That is to say, binary will not stop until here :
11111111111111111111111100000000
So the output is 255.
Here we also found one thing , A signed char The range of types is 0~127 and -1~-128
Unsigned char The type range is 0~255.
// Code 7
#include <stdio.h>
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("hello world\n");
}
return 0;
}
The running result of this code is also an endless loop .
because i yes unsigned char type , No matter what i How to add , All positive numbers. , So the dead cycle .
3. Floating point storage in memory
Common floating point numbers :
3.14159
1E10
The family of floating-point numbers includes : float、double、long double type .
The range represented by floating point numbers :float.h In the definition of
3.1 An example
Examples of floating point storage :
#include <stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
*pFloat = 9.0;
printf("num The value of is :%d\n", n);
printf("*pFloat The value of is :%f\n", *pFloat);
return 0;
}
Our output is :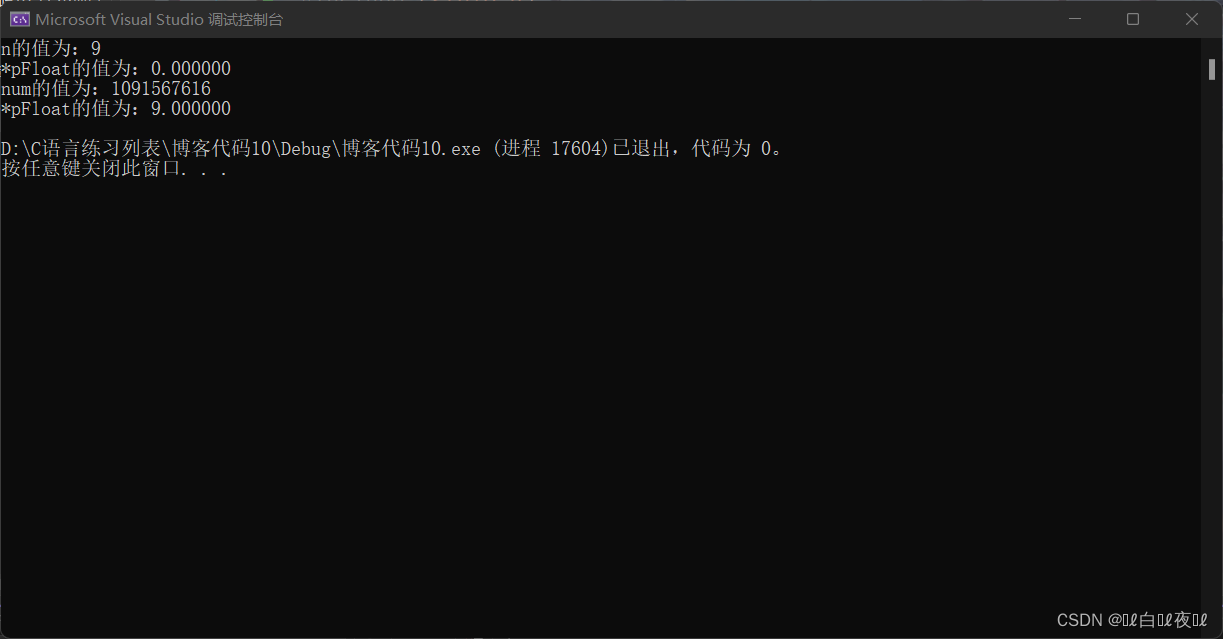
Is the actual result very inconsistent with our expected result ?
Why is that ? Let's look down :
3.2 Floating point storage rules
num and *pFloat It's the same number in memory , Why are the interpretation results of floating-point numbers and integers so different ?
To understand this result , Be sure to understand the representation of floating-point numbers in the computer .
Detailed interpretation :
According to international standards IEEE( Institute of electrical and Electronic Engineering ) 754, Any binary floating point number V It can be expressed in the following form :
(-1)^S * M * 2^E
(-1)^S The sign bit , When S=0,V Is a positive number ; When S=1,V It's a negative number .
M Represents a significant number , Greater than or equal to 1, Less than 2.
2^E Indicates the index bit .
for instance :
Decimal 5.0, Written as binary is 101.0 , amount to 1.01×2^2 .
that , According to the above V The format of , We can draw S=0,M=1.01,E=2.
Decimal -5.0, Written as binary is -101.0 , amount to -1.01×2^2 . that ,S=1,M=1.01,E=2.
IEEE 754 Regulations :
about 32 Floating point number of bits , The highest 1 Bits are sign bits s, And then 8 Bits are exponents E, The rest 23 Bits are significant numbers M.
about 64 Floating point number of bits , The highest 1 Bits are sign bits S, And then 11 Bits are exponents E, The rest 52 Bits are significant numbers M.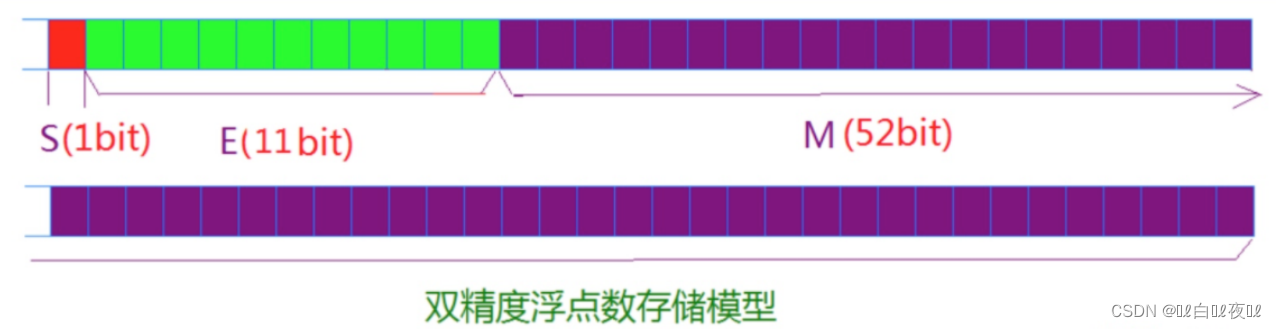
IEEE 754 For significant figures M And the index E, There are some special rules .
As I said before , 1≤M<2 , in other words ,M It can be written. 1.xxxxxx In the form of , among xxxxxx Represents the fractional part .
IEEE 754 Regulations , Keep it in the computer M when , By default, the first digit of this number is always 1, So it can be discarded , Save only the back xxxxxx part . For example preservation 1.01 When , Save only 01, Wait until you read , Put the first 1 Add . The purpose of this , It's saving 1 Significant digits . With 32 For example, a floating-point number , Leave to M Only 23 position , Will come first 1 After giving up , It's equivalent to being able to save 24 Significant digits .
As for the index E, The situation is more complicated .
First ,E For an unsigned integer (unsigned int)
It means , If E by 8 position , Its value range is 0 ~ 255; If E by 11 position , Its value range is 0 ~ 2047. however , We know , In scientific counting E You can have negative numbers , therefore IEEE 754 Regulations , In memory E The true value of must be added with an intermediate number , about 8 Bit E, The middle number is 127; about 11 Bit E, The middle number is 1023. such as ,2^10 Of E yes 10, So save it as 32 When floating-point numbers are in place , Must be saved as 10+127=137, namely 10001001.
then , Index E Fetching from memory can be further divided into three cases :
E Not all for 0 Or not all of them 1
At this time , Floating point numbers are represented by the following rules , The index E The calculated value of minus 127( or 1023), Get the real value , And then the significant number M Add the first 1.
such as :
0.5(1/2) The binary form of is 0.1, Since it is stipulated that the positive part must be 1, That is to move the decimal point to the right 1 position , Then for 1.0*2^(-1), Its order code is -1+127=126, Expressed as
01111110, And the mantissa 1.0 Remove the integer part and make it 0, A filling 0 To 23 position 00000000000000000000000, Then its binary representation is :
0 01111110 00000000000000000000000
E All for 0
At this time , The exponent of a floating point number E be equal to 1-127( perhaps 1-1023) That's the true value , Significant figures M No more first 1, It's reduced to 0.xxxxxx Decimals of . This is to show that ±0, And close to 0 A very small number of .
E All for 1
At this time , If the significant number M All for 0, Express ± infinity ( It depends on the sign bit s);
This is how floating-point data is stored .
Explain the previous topic :
below , Let's go back to the initial question : Why? 0x00000009 Restore to floating point number , became 0.000000 ?
First , take 0x00000009 Split , Get the first sign bit s=0, Back 8 Bit index E=00000000 , Last 23 A significant number of bits M=000 0000 0000 0000 0000 1001.
9 -> 0000 0000 0000 0000 0000 0000 0000 1001
Because the index E All for 0, So the second case in the previous section . therefore , Floating point numbers V The just :
V=(-1)^0 × 0.00000000000000000001001×2^(-126)=1.001×2^(-146)
obviously ,V It's a very small one, close to 0 Positive number of , So the decimal number is 0.000000.(%f Print only after the decimal point 6 The number of bits )
Let's look at the second part of the example .
Floating point number 9.0, How to express... In binary ? How much is it to restore to decimal ?
First , Floating point numbers 9.0 Equal to binary 1001.0, namely 1.001×2^3.
9.0 -> 1001.0 ->(-1)^01.0012^3 -> s=0, M=1.001,E=3+127=130
that , The first sign bit s=0, Significant figures M be equal to 001 Add... To the back 20 individual 0, Cramming 23 position , Index E be equal to 3+127=130, namely 10000010.
therefore , Written in binary form , Should be s+E+M, namely
0 10000010 001 0000 0000 0000 0000 0000
This 32 The binary number of bits , Restore to decimal , It is 1091567616 .
Conclusion
Please give your family a compliment , The big guys don't give enough advice .
边栏推荐
- Tool class: object to map hump to underline underline hump
- Leetcode t1165: log analysis
- 【JDBC以及内部类的讲解】
- Algorithm --- bit count (kotlin)
- How can brand e-commerce grow against the trend? See the future here!
- 弹性布局(二)
- MIPS uclibc cross compile ffmpeg, support g711a encoding and decoding
- Blue Bridge Cup Birthday candles (violence)
- Tumor immunotherapy research prosci Lag3 antibody solution
- 我理想的软件测试人员发展状态
猜你喜欢
Master-slave replication principle of MySQL

. Net 5 fluentftp connection FTP failure problem: this operation is only allowed using a successfully authenticated context

$parent(获取父组件) 和 $root(获取根组件)
Nesting and splitting of components
Anr principle and Practice
Bindingexception exception (error reporting) processing
Special behavior of main function in import statement
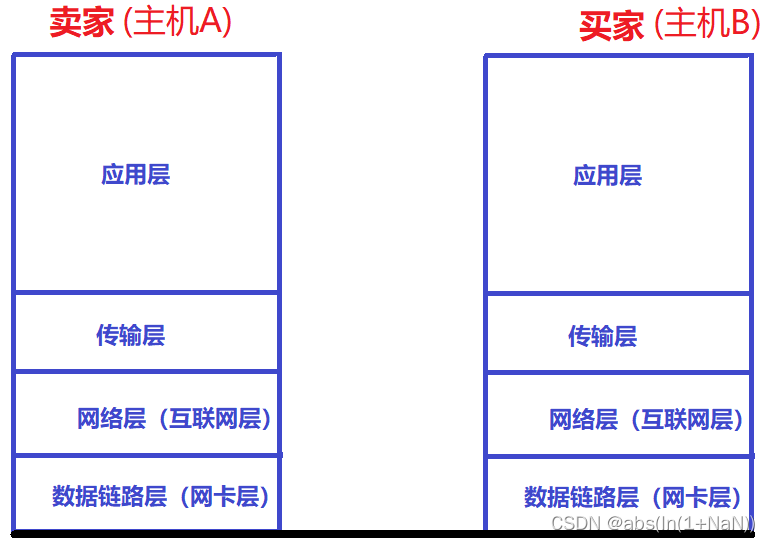
Basic process of network transmission using tcp/ip four layer model
Abnova immunohistochemical service solution

main函数在import语句中的特殊行为
随机推荐
How can clothing stores make profits?
Détailler le bleu dans les tâches de traduction automatique
Initial experience of addresssanitizer Technology
main函数在import语句中的特殊行为
[explanation of JDBC and internal classes]
js小练习
Implementation of AVL tree
云备份项目
Advantages of using net core / why
1090: integer power (multi instance test)
詳解機器翻譯任務中的BLEU
FPGA course: application scenario of jesd204b (dry goods sharing)
Sword finger offer high quality code
Four goals for the construction of intelligent safety risk management and control platform for hazardous chemical enterprises in Chemical Industry Park
Big coffee gathering | nextarch foundation cloud development meetup is coming
Communication of components
mips uclibc 交叉编译ffmpeg,支持 G711A 编解码
父组件传递给子组件:Props
软件验收测试
抽丝剥茧C语言(高阶)数据的储存+练习
