当前位置:网站首页>[exercise -11] 4 values why sum is 0 (and 4 values of 0)
[exercise -11] 4 values why sum is 0 (and 4 values of 0)
2022-07-06 15:57:00 【Flame car】
Description
The SUM problem can be formulated as follows: given four lists A,B,C,D of integer values, compute how many quadruplet (a,b,c,d)∈A×B×C×D are such that a+b+c+d=0. In the following, we assume that all lists have the same size n.
Input
The input begins with a single positive integer on a line by itself indicating the number of the cases following, each of them as described below. This line is followed by a blank line, and there is also a blank line between two consecutive inputs.
The first line of the input file contains the size of the lists n (this value can be as large as 4000). We then have n lines containing four integer values (with absolute value as large as 228) that belong respectively to A,B,C and D.
Output
For each test case, your program has to write the number quadruplets whose sum is zero.
The outputs of two consecutive cases will be separated by a blank line.
Samples
Input
1
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45
Output
5
Hint
Sample Explanation: Indeed, the sum of the five following quadruplets is zero: (-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46), (-32, 30, -75, 77), (-32, -54, 56, 30).
The question :
Enter one per line a,b,c,d, Ask the input a[n],b[n],c[n],d[n] How many combinations can make a+b+c+d=0 establish .
The question is very simple .
First of all, we can definitely think of the enumeration of violence , four layers for loop , But it will obviously time out (4000^4).
This time , You can think of divide and conquer ( Turn the big problem into several small problems ). I can put a+b recorded , Then see if there is -c-d(a+b+c+d=0 ==> a+b = -c-d).
AC Code :
#include<bits/stdc++.h>
using namespace std;
#define CLEAR(a) memset(a,0,sizeof a)
#define Clear(a) memset(a,-1,sizeof a)
typedef long long ll;
const int N = 1e5+5;
const ll mod = 1e9+7;
ll a[4005],b[4005],c[4005],d[4005];
ll tmp[16000005];
int main()
{
int n,t;
ll res;
cin>>t;
while(t--)
{
while (~scanf("%d",&n))
{
res = 0;
for (int i = 0; i < n; i++)
scanf ("%lld%lld%lld%lld", &a[i], &b[i], &c[i], &d[i]);
int cnt = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
tmp[cnt++] = c[i] + d[j];
sort(tmp, tmp + cnt);
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
ll sum =-a[i]-b[j];
res += upper_bound(tmp,tmp+cnt,sum) - lower_bound(tmp,tmp+cnt,sum);
}
printf ("%lld\n\n",res);
}
}
return 0;
}
use scanf To prevent timeout ..
The most important thing here is to understand :
res += upper_bound(tmp,tmp+cnt,sum) - lower_bound(tmp,tmp+cnt,sum);
upper_bound Yes, return greater than ,lower_bound Is to return greater than or equal to . If this time is not equal to , Then it must be 0,(lower = upper = The first one is greater than sum Number of numbers ). But if there is equal to sum The number of will return its number .
You can use this to find The number of a certain number .
边栏推荐
- Learning records: serial communication and solutions to errors encountered
- Penetration test (2) -- penetration test system, target, GoogleHacking, Kali tool
- 【高老师软件需求分析】20级云班课习题答案合集
- STM32 learning record: LED light flashes (register version)
- JS调用摄像头
- 洛谷P1102 A-B数对(二分,map,双指针)
- Learning record: STM32F103 clock system overview working principle
- 【练习-11】4 Values whose Sum is 0(和为0的4个值)
- C语言是低级和高级的分水岭
- Cost accounting [13]
猜你喜欢
![mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’](/img/e6/f4a696179282fe1f4193410c5a493a.png)
mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’

渗透测试 ( 2 ) --- 渗透测试系统、靶机、GoogleHacking、kali工具
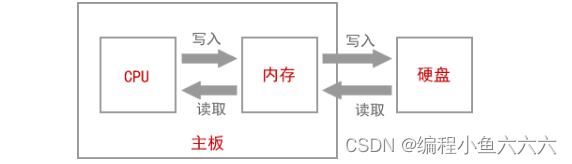
数据在内存中的存储&载入内存,让程序运行起来
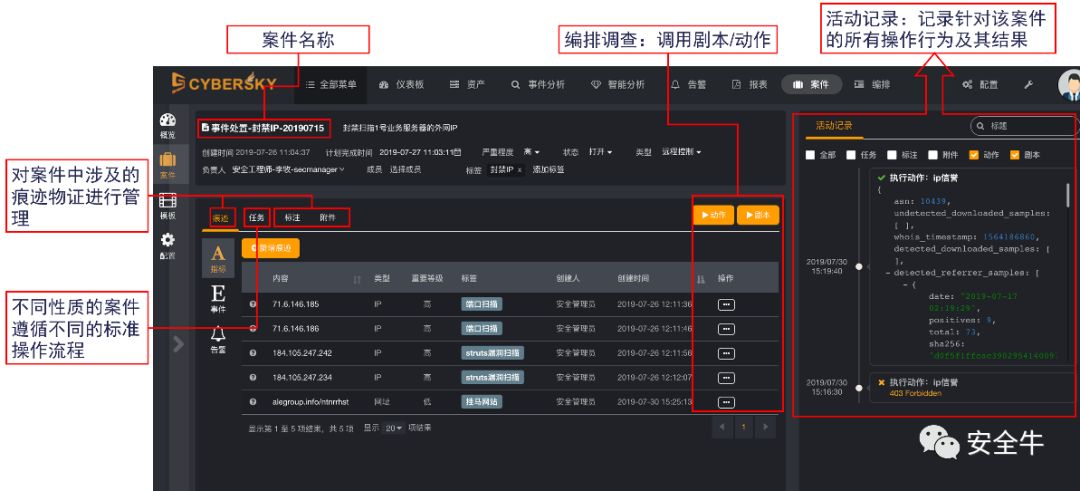
信息安全-安全编排自动化与响应 (SOAR) 技术解析
用C语言写网页游戏
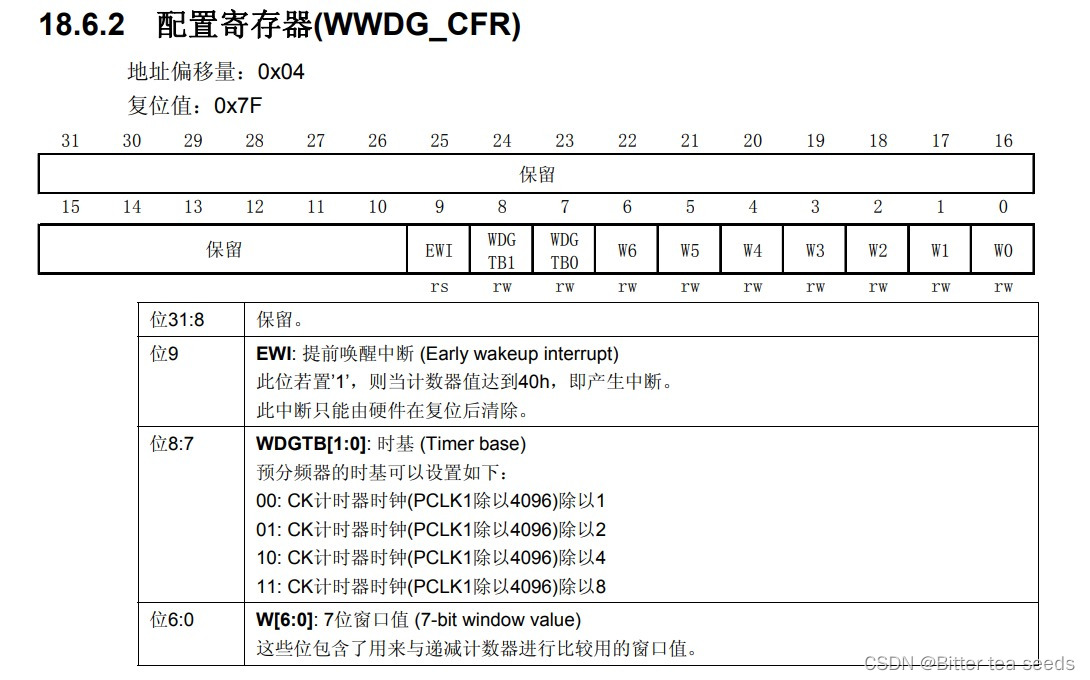
Learning record: use stm32f1 watchdog
Gartner: five suggestions on best practices for zero trust network access
【高老师软件需求分析】20级云班课习题答案合集

Information security - Analysis of security orchestration automation and response (soar) technology

入门C语言基础问答
随机推荐
【练习-6】(PTA)分而治之
Find 3-friendly Integers
【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
C语言是低级和高级的分水岭
E. Breaking the Wall
China earth moving machinery market trend report, technical dynamic innovation and market forecast
信息安全-威胁检测-flink广播流BroadcastState双流合并应用在过滤安全日志
Learning record: use stm32f1 watchdog
信息安全-安全编排自动化与响应 (SOAR) 技术解析
Cost accounting [13]
Opencv learning log 18 Canny operator
Gartner:关于零信任网络访问最佳实践的五个建议
对iptables进行常规操作
Cost accounting [19]
Opencv learning log 31 -- background difference
【高老师软件需求分析】20级云班课习题答案合集
China potato slicer market trend report, technical dynamic innovation and market forecast
D - Function(HDU - 6546)女生赛
【练习-1】(Uva 673) Parentheses Balance/平衡的括号 (栈stack)
Shell脚本编程