Time complexity and space complexity

* The efficiency of the algorithm

After the algorithm is written into an executable program , Runtime needs Waste time, resources and space ( Memory ) resources . So measure the quality of an algorithm , Usually from Time and Space Measured in two dimensions , That is, time complexity and space complexity .
Time complexity mainly measures the performance of an algorithm Running fast or slow , The spatial complexity mainly measures the time required for the operation of an algorithm Extra space . In the early days of computer development , The storage capacity of the computer is very small . So I care about space complexity . But after the rapid development of the computer industry , The storage capacity of the computer has reached a high level . So now we don't need to pay special attention to the spatial complexity of an algorithm

* Time complexity

The time that an algorithm takes to execute , In theory , It can't be worked out , Only you put your program on the machine and run , To know . That's why we have the time complexity analysis . The time taken by an algorithm is proportional to the number of statements executed . In the algorithm Basic operation Number of executions , Time complexity of the algorithm , namely ： Find a basic statement and the scale of the problem N Mathematical expressions between , Is to calculate the time complexity of the algorithm .

* Big O Asymptotic representation of

In practice, when we calculate the time complexity , We don't really have to calculate the exact number of execution , And it only takes about the number of times , Here we use Big O Asymptotic representation of .

Derivation is great O Order method ：
1、 With constant 1 Replace all the addition constants in runtime .
2、 In the modified run times function , Only the highest order terms .
3、 If the highest order term exists and is not 1, The constant multiplied by this item is removed . The result is big O rank .

Big O The progressive representation of Remove those items that have little impact on the results , Simple and clear Indicates the number of executions

In addition, some algorithms have the best time complexity 、 Average and worst case ：
The worst ： Maximum number of runs of any input size ( upper bound )
On average ： Expected number of runs of any input size
The best situation ： Minimum number of runs of any input size ( Lower bound )
for example ： At a length of N Search for a data in the array x
The best situation ：1 Times found
The worst ：N Times found
On average ：N/2 Times found
In practice, the general concern is the worst-case operation of the algorithm , Therefore, the time complexity of searching data in the array is O(N)

* Time complexity of calculation

Here is a well written article that is very helpful to understand the calculation of complexity
example 1：

//  Calculation BubbleSort Time complexity of ？
void BubbleSort(int* a, int n)
{
    
  assert(a);
  for (size_t end = n; end > 0; --end)
  {
    
     int exchange = 0;
     for (size_t i = 1; i < end; ++i)
     {
    
       if (a[i-1] > a[i])
       {
    
         Swap(&a[i-1], &a[i]);
         exchange = 1;
       }
     }
   if (exchange == 0)
   break;
  }
}

example 5 Basic operations perform best N Time , At worst, it's executed (N*(N+1)/2 Time , By deducing the big O Order method + Time complexity is generally the worst , The time complexity is O(N^2)

example 2：

//  Compute factorial recursion Fac Time complexity of ？
long long Fac(size_t N)
{
    
 if(0 == N)
 return 1;
 
 return Fac(N-1)*N;
}

Through calculation and analysis, it is found that the basic operation is recursive N Time , The time complexity is O(N)

example 3：

// Compute Fibonacci recursion Fib Time complexity of ？
long long Fib(size_t N)
{
    
  if(N < 3)
  return 1;
 
  return Fib(N-1) + Fib(N-2);
}

The time complexity can be approximated as 2^N

But strictly speaking In this way

* Spatial complexity

Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation . Space complexity is not how much the program takes up bytes Space , Because it doesn't make much sense either , So the space complexity is the number of open spaces .
The calculation rules of spatial complexity are basically similar to that of time complexity , Also use large O Asymptotic representation .

Be careful ： Stack space required for function runtime ( Store parameters 、 local variable 、 Some register information, etc ) It has been determined during compilation , Therefore, the spatial complexity is mainly determined by the additional space explicitly requested by the function at run time .

* Computational space complexity

example 1：

//  Calculation BubbleSort Spatial complexity of ？
void BubbleSort(int* a, int n)
{
    
   assert(a);
   for (size_t end = n; end > 0; --end)
   {
    
      int exchange = 0;
      for (size_t i = 1; i < end; ++i)
      {
    
        if (a[i-1] > a[i])
        {
    
          Swap(&a[i-1], &a[i]);
          exchange = 1;
        }
      }
     if (exchange == 0)
     break;
   }
}

We've used an extra space , So the space complexity is zero O(1)

example 2：

//  Calculation Fibonacci Spatial complexity of ？
//  Returns the first of the Fibonacci sequence n term 
long long* Fibonacci(size_t n)
{
    
  if(n==0)
  return NULL;
 
  long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
  fibArray[0] = 0;
  fibArray[1] = 1;
  for (int i = 2; i <= n ; ++i)
  {
    
    fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
  }
  return fibArray;
}

Dynamic opens up N Space , The space complexity is O(N)

example 3：

//  Compute factorial recursion Fac Spatial complexity of ？
long long Fac(size_t N)
{
    
  if(N == 0)
  return 1;
 
  return Fac(N-1)*N;
}

example 3 Recursively called N Time , Opens the N Stack frame , Each stack frame uses a constant space . The space complexity is O(N)

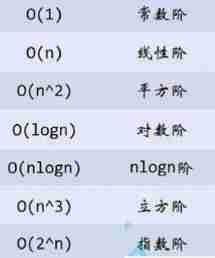
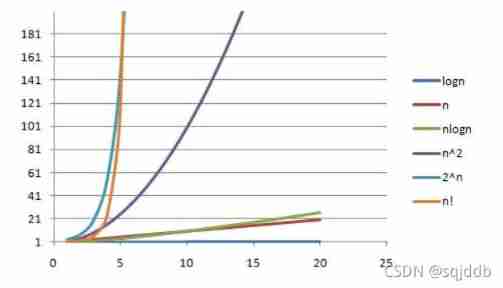
* Complexity comparison