当前位置:网站首页>MATLAB小技巧(28)模糊綜合評價
MATLAB小技巧(28)模糊綜合評價
2022-07-05 08:24:00 【mozun2020】
MATLAB小技巧(28)模糊綜合評價
前言
MATLAB進行圖像處理相關的學習是非常友好的,可以從零開始,對基礎的圖像處理都已經有了封裝好的許多可直接調用的函數,這個系列文章的話主要就是介紹一些大家在MATLAB中常用一些概念函數進行例程演示!
模糊綜合評價法是一種基於模糊數學的綜合評價方法。該綜合評價法根據模糊數學的隸屬度理論把定性評價轉化為定量評價,即用模糊數學對受到多種因素制約的事物或對象做出一個總體的評價。它具有結果清晰,系統性强的特點,能較好地解决模糊的、難以量化的問題,適合各種非確定性問題的解决。
模糊綜合評價法的最顯著特點是:
相互比較
以最優的評價因素值為基准,其評價值為1;其餘欠優的評價因素依據欠優的程度得到相應的評價值。函數關系
可以依據各類評價因素的特征,確定評價值與評價因素值之間的函數關系(即:隸屬度函數)。確定這種函數關系(隸屬度函數)有很多種方法,例如,F統計方法,各種類型的F分布等。當然,也可以請有經驗的評標專家進行評價,直接給出評價值。
在招標文件的編制中,應依據項目的具體情况,有重點地選擇評價因素,科學地確定評價值與評價因素值之間的函數關系以及合理地確定評價因素的權重。模糊綜合評價的一般步驟:
模糊綜合評價指標的構建
模糊綜合評價指標體系是進行綜合評價的基礎,評價指標的選取是否適宜,將直接影響綜合評價的准確性。進行評價指標的構建應廣泛涉獵與該評價指標系統行業資料或者相關的法律法規。采用構建好權重向量
通過專家經驗法或者AHP層次分析法構建好權重向量。構建隸屬矩陣
建立適合的隸屬函數從而構建好隸屬矩陣。隸屬矩陣和權重的合成
采用適合的合成因子對其進行合成,並對結果向量進行解釋。
仿真示例MATLAB版本為MATLAB2015b。
一. MATLAB仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:本程序為模糊綜合評判的程序,人為給定權重
%環境:Win7,Matlab2015b
%Modi: C.S
%時間:2022-06-27
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% I. 清空環境變量
clear all
clc
tic
%--------------------------------------------------------------------------
%程序運行,直接輸入命令mohu即可
%本程序可以進行擴展
%對於進行二級模糊綜合評判,可編制mohufun.m函數來實現
%如[yy1,qdh,qdh1]=mohufun(R,L,M,w,XX,yy]來實現運行兩次這個函數,並編制相應的m文件,其中放至兩個這樣的函數即可實現
%模糊評判的結果說明:
%1:對於所有等級的隸屬度之和為1。
%2:輸出結果隨某個變量的增大而qdh1的結果呈現出單調遞增或遞减
%3:最後的等級出[0.2 0 0 0.8]這種情况是正常的,和可拓評判中的對於等級的距離的概念是不一樣的。
%只錶現有變量是屬於0.2這個等級的。
%--------------------------------------------------------------------------
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%此部分由計算時,人為給定部分,即相關求解條件
%要求計算前輸入部分
R=4; %影響因素的個數
L=4; %評判的等級個數
M=29; %待評價洞段的個數
w=[0.1 0.7 0.1 0.1];%各指標的權重
%可拓評判的經典域,每天列構成一組,共有L組,由左到右依此為1,2,3,4
%評判結果為1,則錶示屬於最左邊的經典域,為4則屬於最右邊的經典域
%XX為隸屬函數的範圍,具體可參見論文基於粗集的模糊綜合評判,一個有四個隸屬函數
%前兩個數,確定是一個下降段的隸屬函數,分成三段
%以後依此4上數為一組,確定一個梯形的隸屬函數,分成五段
%最後兩個是單獨一組,為一個上昇段的隸屬函數分成三段
%下面的每行有12個數,其分成4個等級,分辦界點數個2 4 4 2 之和為12
%也就是構成四個等級範圍
%XX也是計算的核心數據
xx=[70 90 70 90 110 130 110 130 170 190 170 190
45 35 45 35 30 20 30 20 17 10 17 10
1.5 2.5 1.5 2.5 3 4 3 4 4.5 5.5 4.5 5.5
0.25 0.35 0.25 0.35 0.45 0.55 0.45 0.55 0.65 0.75 0.65 0.75];
%pp1為個指標為越大,等級越高,還是越大,等級越小的指標
%0為指標值越大,等級越大
%1為指標值越大,等級越小
%這一點要嚴格執行,XX(i,:),從小到大為0,XX(i,:)從大到小為1,
%若將以上的XX第行的順序顛倒,則為pp1=[1 0 1 1 ]
pp1=[0 1 0 0];
%各待評價洞段參數
yy=[200 8 6 0.8
200 9.5 6 0.8
200 11 6 0.8
200 12.5 6 0.8
200 14 6 0.8
200 15.5 6 0.8
200 17 6 0.8
200 18.5 6 0.8
200 20 6 0.8
200 21.5 6 0.8
200 23 6 0.8
200 24.5 6 0.8
200 26 6 0.8
200 27.5 6 0.8
200 29 6 0.8
200 30.5 6 0.8
200 32 6 0.8
200 33.5 6 0.8
200 35 6 0.8
200 36.5 6 0.8
200 38 6 0.8
200 39.5 6 0.8
200 41 6 0.8
200 42.5 6 0.8
200 44 6 0.8
200 45.5 6 0.8
200 47 6 0.8
200 48.5 6 0.8
200 50 6 0.8
];
%下昇段和下降段的隸屬函數形式
%注意隸屬函數的形式和論文中的隸屬函數形式也要一樣,否則要更改程序中的基些部分
%這裏的a指區間的中間點,b指區間的寬度
f1=inline('0.5-0.5*sin((x-a)*pi/b)','a','b','x');
f2=inline('0.5+0.5*sin((x-a)*pi/b)','a','b','x');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每個指標對於第一個等級的隸屬度
for i=1:M,
for k=1:R,
j=1;
if pp1(k)==0 %先是求越大,等級越高的指標
if yy(i,k)<xx(k,j)
yy1(i,k,j)=1;
elseif yy(i,k)<=xx(k,j+1)
yy1(i,k,j)=f1(0.5*(xx(k,j)+xx(k,j+1)),abs(xx(k,j)-xx(k,j+1)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
%再是求值越小,等級越高的指標
%下在和一個相比大於和小於要互換,函數f1和f2也要互換
elseif yy(i,k)>xx(k,j)
yy1(i,k,j)=1;
elseif yy(i,k)>=xx(k,j+1)
yy1(i,k,j)=f2(0.5*(xx(k,j)+xx(k,j+1)),abs(xx(k,j)-xx(k,j+1)),yy(i,k));
else yy1(i,k,j)=0;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每個指標對於最後一個等級的隸屬度
for i=1:M,
for k=1:R,
j=L;
if pp1(k)==0 %先是求越大,等級越高的指標
if yy(i,k)<xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)<=xx(k,j*4-4)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
else yy1(i,k,j)=1;
end
%再是求值越小,等級越高的指標
%下在和一個相比大於和小於要互換,函數f1和f2也要互換
elseif yy(i,k)>xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)>=xx(k,j*4-4)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k)) ;
else yy1(i,k,j)=1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求每個指標對於中間幾個等級的隸屬度
for i=1:M,
for k=1:R,
for j=2:L-1;
if pp1(k)==0 %先是求越大,等級越高的指標
if yy(i,k)<xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)<=xx(k,j*4-4)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
elseif yy(i,k)<=xx(k,j*4-3)
yy1(i,k,j)=1;
elseif yy(i,k)<=xx(k,j*4-2)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-3)+xx(k,j*4-2)),abs(xx(k,j*4-3)-xx(k,j*4-2)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
%再是求值越小,等級越高的指標
%下在和一個相比大於和小於要互換,函數f1和f2也要互換
elseif yy(i,k)>xx(k,j*4-5)
yy1(i,k,j)=0;
elseif yy(i,k)>=xx(k,j*4-4)
yy1(i,k,j)=f1(0.5*(xx(k,j*4-5)+xx(k,j*4-4)),abs(xx(k,j*4-5)-xx(k,j*4-4)),yy(i,k));
elseif yy(i,k)>=xx(k,j*4-3)
yy1(i,k,j)=1;
elseif yy(i,k)>=xx(k,j*4-2)
yy1(i,k,j)=f2(0.5*(xx(k,j*4-3)+xx(k,j*4-2)),abs(xx(k,j*4-3)-xx(k,j*4-2)),yy(i,k)) ;
else yy1(i,k,j)=0;
end
end
end
end
% %相乘計算,隸屬度乘權重各洞段對每一等級的隸屬度,取最大值
%dot函數為內積函數,為兩向量各對應分量相等後再求和
for i=1:M,
for j=1:L,
qdh(i,j)=dot(yy1(i,:,j),w);
end
end
%隸屬度乘等級值,確定級別
% %qdh為評價結果,取最大的,屬於哪一個等級
% qdh1,等級值
for i=1:M,
for j=1:L,
[maxlevel(i),qdh1(i)]=max(qdh(i,:));
end
disp(['樣本',num2str(i),'對應分類為:',num2str(qdh1(i))]);
end
figure(1)
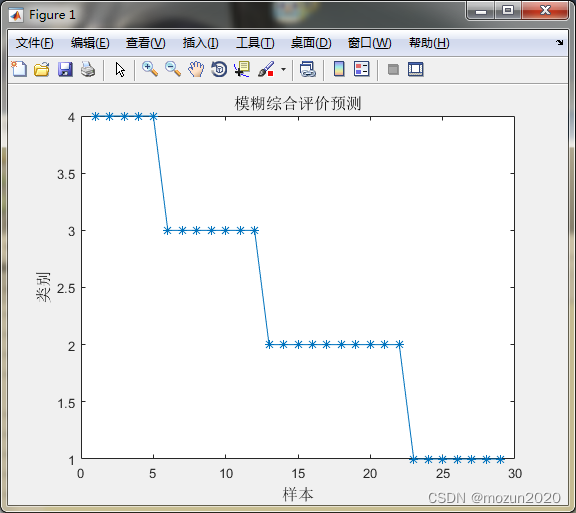
plot(qdh1(1:29),'-*');
title('模糊綜合評價預測','fontsize',12)
xlabel('樣本','fontsize',12)
ylabel('類別','fontsize',12)
toc
二. 仿真結果
樣本1對應分類為:4
樣本2對應分類為:4
樣本3對應分類為:4
樣本4對應分類為:4
樣本5對應分類為:4
樣本6對應分類為:3
樣本7對應分類為:3
樣本8對應分類為:3
樣本9對應分類為:3
樣本10對應分類為:3
樣本11對應分類為:3
樣本12對應分類為:3
樣本13對應分類為:2
樣本14對應分類為:2
樣本15對應分類為:2
樣本16對應分類為:2
樣本17對應分類為:2
樣本18對應分類為:2
樣本19對應分類為:2
樣本20對應分類為:2
樣本21對應分類為:2
樣本22對應分類為:2
樣本23對應分類為:1
樣本24對應分類為:1
樣本25對應分類為:1
樣本26對應分類為:1
樣本27對應分類為:1
樣本28對應分類為:1
樣本29對應分類為:1
時間已過 0.075994 秒。
三. 小結
模糊綜合評價法(fuzzy comprehensive evaluation method)是模糊數學中最基本的數學方法之一,該方法是以隸屬度來描述模糊界限的。由於評價因素的複雜性、評價對象的層次性、評價標准中存在的模糊性以及評價影響因素的模糊性或不確定性、定性指標難以定量化等一系列問題,使得人們難以用絕對的“非此即彼”來准確的描述客觀現實,經常存在著“亦此亦彼”的模糊現象,其描述也多用自然語言來錶達,而自然語言最大的特點是它的模糊性,而這種模糊性很難用經典數學模型加以統一量度。因此,建立在模糊集合基礎上的模糊綜合評判方法,從多個指標對被評價事物隸屬等級狀况進行綜合性評判,它把被評判事物的變化區間做出劃分,一方面可以顧及對象的層次性,使得評價標准、影響因素的模糊性得以體現;另一方面在評價中又可以充分發揮人的經驗,使評價結果更客觀,符合實際情况。模糊綜合評判可以做到定性和定量因素相結合,擴大信息量,使評價數度得以提高,評價結論可信。
傳統的綜合評價方法很多,應用也較為廣泛,但是沒有一種方法能够適合各種場所,解决所有問題,每一種方法都有其側重點和主要應用領域。如果要解决新的領域內產生的新問題,模糊綜合法顯然更為合適。模糊評價法奠基於模糊數學。模糊數學誕生於1965年,他的創始人美國自動控制專家L.A.Zadeh。20世紀80年代後期,日本將模糊技術應用於機器人、過程控制、地鐵機車、交通管理、故障診斷、醫療診斷、聲音識別、圖像處理、市場預測等眾多領域。模糊理論及模糊法在日本的應用和巨大的市場前景,給西方企業界很大震動,在學術界也得到了普遍的認同。國內對於模糊數學及模糊綜合評價法的研究起步相對較晚,但在近些年各個領域(如醫學、建築業、環境質量監督、水利等)的應用也已初顯成效。每天學一個MATLAB小知識,大家一起來學習進步阿!
边栏推荐
- 99 multiplication table (C language)
- Stm32--- systick timer
- 剑指 Offer 09. 用两个栈实现队列
- 实例010:给人看的时间
- Live555 push RTSP audio and video stream summary (I) cross compilation
- 实例001:数字组合 有四个数字:1、2、3、4,能组成多少个互不相同且无重复数字的三位数?各是多少?
- QEMU STM32 vscode debugging environment configuration
- My-basic application 1: introduction to my-basic parser
- Example 009: pause output for one second
- STM32---IIC
猜你喜欢
leetcode - 445. 两数相加 II
实例009:暂停一秒输出
Negative pressure generation of buck-boost circuit
实例003:完全平方数 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
Matlab2018b problem solving when installing embedded coder support package for stmicroelectronic

Example 006: Fibonacci series
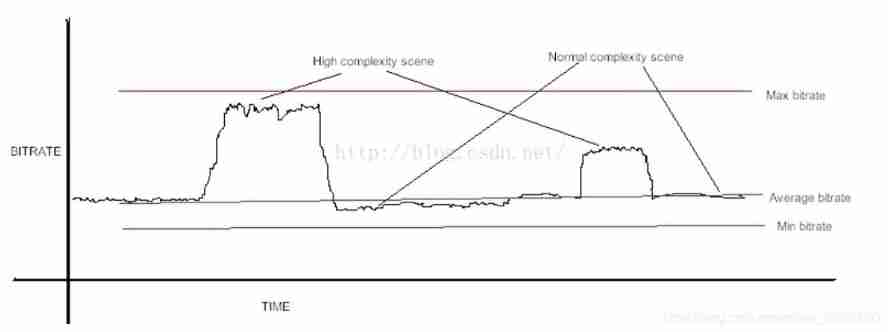
H264 (I) i/p/b frame gop/idr/ and other parameters
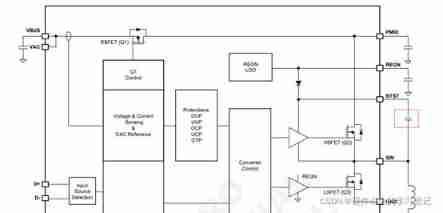
DCDC circuit - function of bootstrap capacitor
99 multiplication table (C language)

实例002:“个税计算” 企业发放的奖金根据利润提成。利润(I)低于或等于10万元时,奖金可提10%;利润高于10万元,低于20万元时,低于10万元的部分按10%提成,高于10万元的部分,可提成7.
随机推荐
H264 (I) i/p/b frame gop/idr/ and other parameters
Live555 push RTSP audio and video stream summary (III) flower screen problem caused by pushing H264 real-time stream
[paper reading] the latest transfer ability in deep learning: a survey in 2022
Management and use of DokuWiki (supplementary)
Infected Tree(树形dp)
实例007:copy 将一个列表的数据复制到另一个列表中。
Example 005: three numbers sorting input three integers x, y, Z, please output these three numbers from small to large.
Verilog -- state machine coding method
Soem EtherCAT source code analysis I (data type definition)
Several important parameters of LDO circuit design and type selection
[trio basic from introduction to mastery tutorial 20] trio calculates the arc center and radius through three points of spatial arc
Briefly talk about the identification protocol of mobile port -bc1.2
Take you to understand the working principle of lithium battery protection board
STM32 summary (HAL Library) - DHT11 temperature sensor (intelligent safety assisted driving system)
STM32 --- configuration of external interrupt
Stm32--- systick timer
STM32 single chip microcomputer -- debug in keil5 cannot enter the main function
Sql Server的存储过程详解
QEMU STM32 vscode debugging environment configuration
Naming rules for FreeRTOS