当前位置:网站首页>A detailed explanation of vector derivative and matrix derivative
A detailed explanation of vector derivative and matrix derivative
2022-07-03 10:40:00 【serity】
Catalog
Vector derivative and matrix derivative are the mathematical basis of machine learning , Read this article carefully , I believe you will have a lot to gain ~
carry And towards The amount when , if nothing , Especially say bright , I People Silent recognize by Column towards The amount \textcolor{red}{ When it comes to vectors , Unless otherwise specified , We default to {\bf Column vector }} carry And towards The amount when , if nothing , Especially say bright , I People Silent recognize by Column towards The amount
One 、 Numerator layout and denominator layout
We know , Scalar (Scalar)、 vector (Vector) And matrices (Matrix) The three of them meet the following relationship :
mark The amount ⊂ towards The amount ⊂ Moment front Scalar \subset vector \subset matrix mark The amount ⊂ towards The amount ⊂ Moment front
That is, a vector can be understood as a special matrix ( The number of columns is 1 1 1 Matrix ), Scalar can be understood as a special vector ( Dimension for 1 1 1 Vector ), It can also be understood as a 1 × 1 1\times 1 1×1 Matrix , So the vector derivative and matrix derivative we are discussing today can be collectively referred to as “ Matrix derivative ”.
There are six common matrix derivatives :
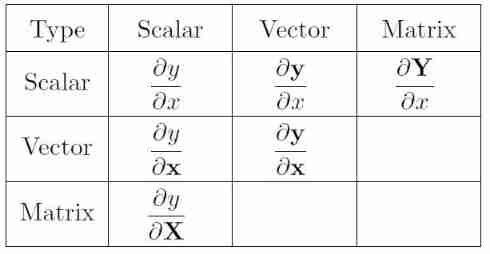
Scalar derivative of scalar is familiar to everyone ( f ′ ( x ) f'(x) f′(x) It's a typical example ), We won't discuss it here . In fact, we can also discuss the derivative between matrix and vector , Derivative between matrices , That is, where the table is empty , But because the results of these derivatives involve dimensions greater than 2 2 2 Tensor (tensor), We can no longer express in the form of matrix , Therefore, we will not discuss .
Next, we will focus on the remaining five matrix derivatives , namely :
- Vector derivative of scalar
- Scalar derivative of vector
- Vector to vector derivation
- Matrix derivative of scalar
- Scalar derivative of matrix
Suppose we have x = ( x 1 , ⋯ , x n ) T \boldsymbol{x}=(x_1,\cdots,x_n)^{\mathrm T} x=(x1,⋯,xn)T and y = ( y 1 , ⋯ , y m ) T \boldsymbol{y}=(y_1,\cdots,y_m)^{\mathrm T} y=(y1,⋯,ym)T Two vectors , be ∂ y ∂ x \displaystyle \frac{\partial \boldsymbol{y}}{\partial \boldsymbol{x}} ∂x∂y share m n mn mn Weight :
∂ y i ∂ x j , i = 1 , ⋯ , m j = 1 , ⋯ , n \frac{\partial y_i}{\partial x_j},\quad i=1,\cdots,m\quad j=1,\cdots,n ∂xj∂yi,i=1,⋯,mj=1,⋯,n
How should we arrange this m n mn mn How many components ? That's what we need Molecular arrangement (Numerator Layout) and Denominator layout (Denominator Layout) 了 . The so-called layout , It is nothing more than an arrangement of the above results , If the arrangement is not specified , It is likely to cause errors in the process of mathematical operations ( For example, due to the dimension of the matrix, it cannot be multiplied ).
When talking about vector derivatives , We have two very important premises :
① Molecules and denominators Is a vector , And one of them is Row vector , The other is Column vector
② One of the numerator and denominator is Scalar , The other is That's ok / Column vector
When ① or ② When satisfied , Our next discussion is meaningful .
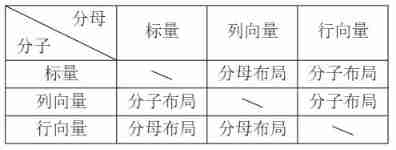
We see first ①:
- If denominator is column vector , Molecules are row vectors , It is called denominator layout
- If the molecule is a column vector , The denominator is the row vector , It is called molecular layout
In a word, it is : Who is the column vector is what layout .
about ②, We can still use “ Who is the column vector is what layout ” To judge , But if the numerator and denominator are not column vectors , How to judge ?
This situation is also summarized in one sentence : Who is scalar is what layout .
We can summarize these discussions in the following table :
about Matrix derivative , Things are a little different :

Besides , We also have the following Important equation :
branch Son cloth game Of junction fruit = branch mother cloth game Of junction fruit T , branch mother cloth game Of junction fruit = branch Son cloth game Of junction fruit T The result of molecular layout = The result of the denominator layout ^{\mathrm{T}},\qquad The result of the denominator layout = The result of molecular layout ^{\mathrm{T}} branch Son cloth game Of junction fruit = branch mother cloth game Of junction fruit T, branch mother cloth game Of junction fruit = branch Son cloth game Of junction fruit T
All the above results can be summarized into the following three figures :



More intuitive expression :
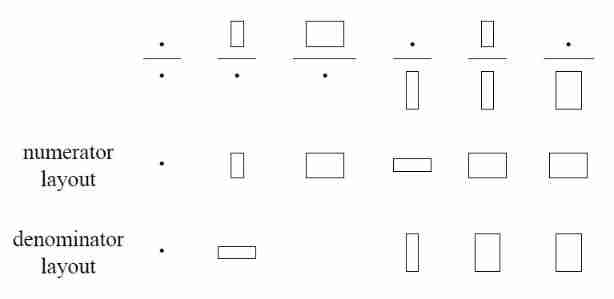
Our next discussion will be based on Molecular arrangement .
Two 、 Vector derivative
2.1 Vector derivative of scalar
Some rules for the derivation of vectors from scalars :

2.2 Scalar derivative of vector
Some rules of scalar derivation from vector :

Some of scalar derivatives of vectors Important conclusions :
∂ a ∂ x = 0 T (2.2.A) \frac{\partial a }{\partial \boldsymbol x}={\bf 0}^{\mathrm T}\tag{2.2.A} ∂x∂a=0T(2.2.A)
∂ a T x ∂ x = ∂ x T a ∂ x = a T (2.2.B) \frac{\partial \boldsymbol a^{\mathrm T}\boldsymbol x }{\partial \boldsymbol x}=\frac{\partial \boldsymbol x^{\mathrm T}\boldsymbol a }{\partial \boldsymbol x}=\boldsymbol a^{\mathrm T} \tag{2.2.B} ∂x∂aTx=∂x∂xTa=aT(2.2.B)
∂ x T x ∂ x = 2 x T (2.2.C) \frac{\partial \boldsymbol x^{\mathrm T}\boldsymbol x }{\partial \boldsymbol x}=2\boldsymbol x^{\mathrm T} \tag{2.2.C} ∂x∂xTx=2xT(2.2.C)
∂ x T A x ∂ x = x T ( A + A T ) (2.2.D) \frac{\partial \boldsymbol x^{\mathrm T}{\bf A}\boldsymbol x }{\partial \boldsymbol x}=\boldsymbol x^{\mathrm T}({\bf A}+{\bf A}^{\mathrm T}) \tag{2.2.D} ∂x∂xTAx=xT(A+AT)(2.2.D)
2.3 Vector to vector derivation
Some rules of vector to vector derivation :

Some of the derivatives of vectors Important conclusions :
∂ a ∂ x = O (2.3.A) \frac{\partial \boldsymbol a }{\partial \boldsymbol x}={\bf O}\tag{2.3.A} ∂x∂a=O(2.3.A)
∂ x ∂ x = I (2.3.B) \frac{\partial \boldsymbol x }{\partial \boldsymbol x}={\bf I}\tag{2.3.B} ∂x∂x=I(2.3.B)
∂ A x ∂ x = A (2.3.C) \frac{\partial {\bf A}\boldsymbol x }{\partial \boldsymbol x}={\bf A}\tag{2.3.C} ∂x∂Ax=A(2.3.C)
3、 ... and 、 Matrix derivative
3.1 Matrix derivative of scalar
Some rules of matrix deriving scalar :

3.2 Scalar derivative of matrix
Some rules of scalar matrix derivation :

Some of scalar derivation of matrix Important conclusions :
∂ a ∂ X = O (3.2.A) \frac{\partial a }{\partial {\bf X}}={\bf O}\tag{3.2.A} ∂X∂a=O(3.2.A)
∂ a T X b ∂ X = b a T (3.2.B) \frac{\partial \boldsymbol a^{\mathrm T}{\bf X}\boldsymbol b }{\partial {\bf X}}=\boldsymbol{ba}^{\mathrm T}\tag{3.2.B} ∂X∂aTXb=baT(3.2.B)
∂ a T X T b ∂ X = a b T (3.2.C) \frac{\partial \boldsymbol a^{\mathrm T}{\bf X}^{\mathrm T}\boldsymbol b }{\partial {\bf X}}=\boldsymbol{ab}^{\mathrm T}\tag{3.2.C} ∂X∂aTXTb=abT(3.2.C)
Besides , We often encounter the derivation of trace pair matrix , Relevant conclusions are as follows :
∂ t r ( X ) ∂ X = I (3.2.D) \frac{\partial \mathrm{tr}({\bf X})}{\partial {\bf X}}={\bf I}\tag{3.2.D} ∂X∂tr(X)=I(3.2.D)
∂ t r ( X k ) ∂ X = k X k − 1 (3.2.E) \frac{\partial \mathrm{tr}({\bf X}^{k})}{\partial {\bf X}}=k{\bf X}^{k-1}\tag{3.2.E} ∂X∂tr(Xk)=kXk−1(3.2.E)
∂ t r ( A X ) ∂ X = ∂ t r ( X A ) ∂ X = A (3.2.F) \frac{\partial \mathrm{tr}({\bf AX})}{\partial {\bf X}}=\frac{\partial \mathrm{tr}({\bf XA})}{\partial {\bf X}}={\bf A}\tag{3.2.F} ∂X∂tr(AX)=∂X∂tr(XA)=A(3.2.F)
∂ t r ( A X T ) ∂ X = ∂ t r ( X T A ) ∂ X = A T (3.2.G) \frac{\partial \mathrm{tr}({\bf AX}^{\mathrm T})}{\partial {\bf X}}=\frac{\partial \mathrm{tr}({\bf X}^{\mathrm T}{\bf A})}{\partial {\bf X}}={\bf A}^{\mathrm T}\tag{3.2.G} ∂X∂tr(AXT)=∂X∂tr(XTA)=AT(3.2.G)
∂ t r ( X T A X ) ∂ X = X T ( A + A T ) (3.2.H) \frac{\partial \mathrm{tr}({\bf X}^{\mathrm T}{\bf AX})}{\partial {\bf X}}={\bf X}^{\mathrm T}({\bf A}+{\bf A}^{\mathrm T})\tag{3.2.H} ∂X∂tr(XTAX)=XT(A+AT)(3.2.H)
∂ t r ( X − 1 A ) ∂ X = − X − 1 A X − 1 (3.2.I) \frac{\partial \mathrm{tr}({\bf X}^{-1}{\bf A})}{\partial {\bf X}}=-{\bf X}^{-1}{\bf AX}^{-1}\tag{3.2.I} ∂X∂tr(X−1A)=−X−1AX−1(3.2.I)
∂ t r ( A X B ) ∂ X = ∂ t r ( B A X ) ∂ X = B A (3.2.J) \frac{\partial \mathrm{tr}({\bf AXB})}{\partial {\bf X}}=\frac{\partial \mathrm{tr}({\bf BAX})}{\partial {\bf X}}={\bf BA}\tag{3.2.J} ∂X∂tr(AXB)=∂X∂tr(BAX)=BA(3.2.J)
∂ t r ( A X B X T C ) ∂ X = B X T C A + B T X T A T C T (3.2.K) \frac{\partial \mathrm{tr}({\bf AXBX}^{\mathrm T}{\bf C})}{\partial {\bf X}}={\bf BX}^{\mathrm T}{\bf CA}+{\bf B}^{\mathrm T}{\bf X}^{\mathrm T}{\bf A}^{\mathrm T}{\bf C}^{\mathrm T} \tag{3.2.K} ∂X∂tr(AXBXTC)=BXTCA+BTXTATCT(3.2.K)
Reference resources
[1] https://zhuanlan.zhihu.com/p/263777564
[2] https://www.zhihu.com/question/352174717
[3] https://cloud.tencent.com/developer/article/1551901
[4] https://en.wikipedia.org/wiki/Matrix_calculus
[5] https://www.comp.nus.edu.sg/~cs5240/lecture/matrix-diff.pdf
边栏推荐
- 2-program logic
- Leetcode skimming ---202
- Handwritten digit recognition: CNN alexnet
- Leetcode skimming ---278
- R language classification
- Convolutional neural network (CNN) learning notes (own understanding + own code) - deep learning
- A super cool background permission management system
- The imitation of jd.com e-commerce project is coming
- 二分查找法
- Realize an online examination system from zero
猜你喜欢

Ut2012 learning notes

Knowledge map enhancement recommendation based on joint non sampling learning

7、 Data definition language of MySQL (2)
Entropy method to calculate weight
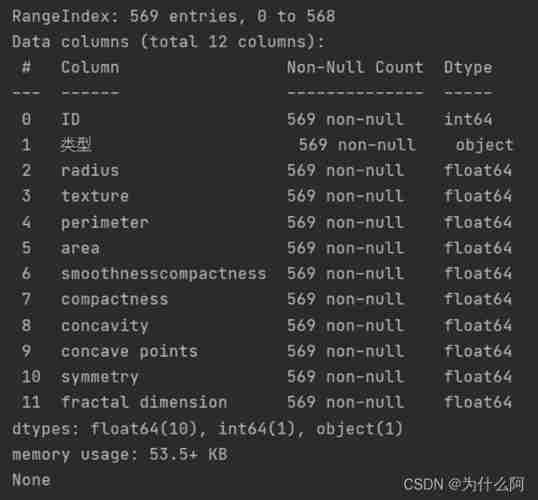
Data classification: support vector machine
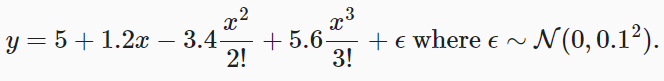
Model selection for neural network introduction (pytorch)

Configure opencv in QT Creator
GAOFAN Weibo app

Free online markdown to write a good resume
The story of a 30-year-old tester struggling, even lying flat is extravagant
随机推荐
Leetcode skimming ---44
Leetcode skimming ---75
7、 Data definition language of MySQL (2)
Leetcode刷题---852
Adaptive Propagation Graph Convolutional Network
Multilayer perceptron (pytorch)
Notes - regular expressions
Out of the box high color background system
一个30岁的测试员无比挣扎的故事,连躺平都是奢望
神经网络入门之预备知识(PyTorch)
Weight decay (pytorch)
OpenCV Error: Assertion failed (size.width>0 && size.height>0) in imshow
Unity小组工程实践项目《最强外卖员》策划案&纠错文档
Leetcode刷题---44
High imitation bosom friend manke comic app
Free online markdown to write a good resume
Type de contenu « Application / X - www - form - urlencoded; Charset = utf - 8 'not supported
Numpy Foundation
Training effects of different data sets (yolov5)
2018 Lenovo y7000 black apple external display scheme