Model selection for neural network introduction (pytorch)

https://courses.d2l.ai/zh-v2/

Model selection

Training error and generalization error

• Training error ： The error of the model in the training data
• The generalization error ： Model error on new data
• Example ： Predict future test scores based on model test scores
  • Did well in the past exam （ Training error ） It doesn't mean that the future exam must be very good （ The generalization error ）
  • Student A Get a good score in the model exam through endorsement
  • Student B Know the reason behind the answer

Validation data sets and test data sets

• Validation data set ： A data set used to evaluate the quality of the model
  • For example, take out 50% Training data
  • Don't mix with training data （ Often make mistakes ）
• Test data set ： A data set used only once . for example
  • Future exams
  • The actual transaction price of the house I bid
  • Use in Kaggle Data set in private ranking board

• Because the validation data set did not participate in the training , To some extent, it can reflect the quality of the model's superparameter selection
• Validation data set and training data must not be mixed

K- Then cross verify

• Use when there is not enough data （ This is the norm ）
• Algorithm ：
  • Split the training data into K fast
  • For i =1,…,K
    • Use the i Block as validation data set , The rest are used as training data sets
  • The report K The average error of the validation data set
• Commonly used ：K=5 or 10

validation dataset Test data set

summary

• Training data set ： Training model parameters
• Validation data set ： Select model superparameters
• Usually used on non large data sets k- Crossover verification

k- Crossover verification （k-fold cross-validation）
Divide into K Share , do K Time , Keep one copy each time for verification , The rest as a training set
To pass K The average error of the fold is used to judge the quality of the superparameter

Over fitting and under fitting

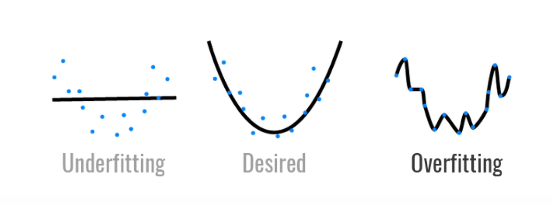
capacity Capacity , It can also be understood as ability

Model capacity

• Ability to fit various functions
• Low volume models are difficult to fit training data
• The high-capacity model can remember all the training data

Selection of model capacity

Higher order polynomial functions are much more complex than lower order polynomial functions . There are many parameters of higher-order polynomials , The selection range of model functions is wide . Therefore, in the case of fixed training data set , The training error of higher-order polynomial function should always be lower than that of lower order polynomial （ The worst is equal ）. in fact , When the data sample contains $x$ When different values of , The polynomial function whose order is equal to the number of data samples can perfectly fit the training set .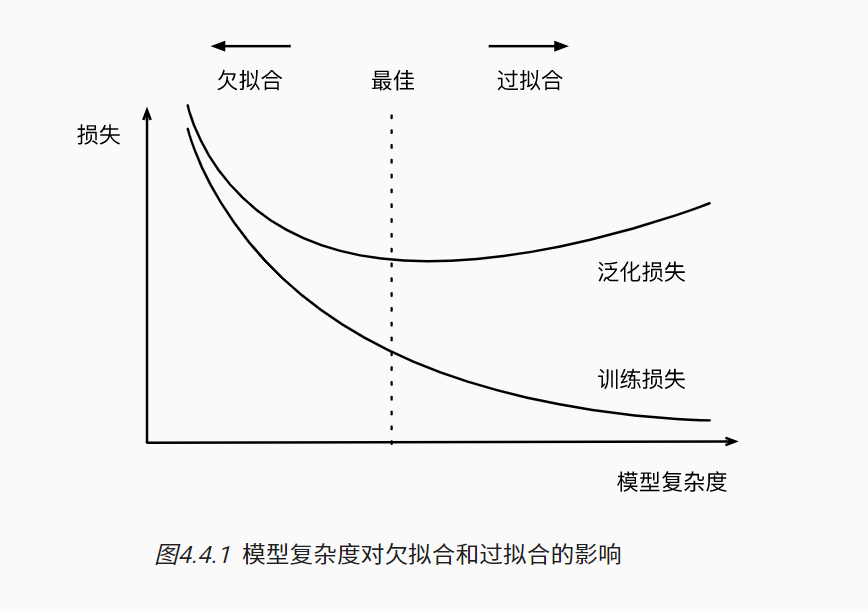

Estimate model capacity

• It is difficult to compare different kinds of algorithms
  • For example, tree model and neural network
• Given a model type , There will be two main parameters
  • Number of parameters
  • Selection range of parameter values

The number of parameters of the linear model is d+1 ,1 Is the offset of the parameter

VC dimension

• A core idea of statistical learning theory
• For a classification model ,VC Equal to the size of a largest dataset , No matter how the label is given , There is a model to classify it perfectly

Lin Xuantian spoke very well (vc dimension),<< Building blocks of machine learning >>

Linear classifier's VC dimension

• 2 Perceptron of dimension input ,VC dimension =3

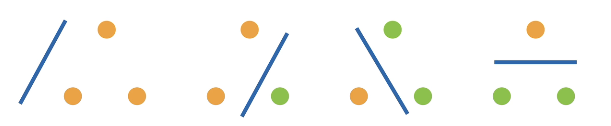
  • Be able to classify any three points , But it's not 4 individual (xor)
    
    

• Support N Dimension input of the perceptron VC Weishi N+1

• Some multi-layer perceptron VC dimension $O(Nlo{g}_{2}N)$

2 For input perceptron means , The input characteristics are 2, The output is 1

VC Use of dimension

• Provide a theoretical basis for why a model is good
  • It can measure the interval between training error and generalization error
• But it is rarely used in deep learning
  • The measurement is not very accurate
  • Calculate the depth of learning model VC It's difficult

Data complexity

• Several important factors
  • Number of samples
  • Number of elements per sample
  • Time 、 Spatial structure
  • diversity

summary

• The model capacity needs to match the data complexity , Otherwise, it may lead to under fitting and over fitting
• Statistical machine learning provides mathematical tools to measure model complexity
• In practice, training error and verification error are usually observed

Code

Polynomial regression

Explore these concepts through polynomial fitting

import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l

Generate data set

Given , We will use the following third-order polynomials to generate labels for training and test data ：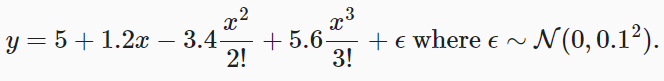

Noise term $ϵ$ To obey the mean is 0 And the standard deviation is 0.1 Is a normal distribution . In the process of optimization , We usually want to avoid very large gradient values or loss values . That's why we're going to change the characteristics from $x^i$ Adjusted for $\frac{x^i}{i!}$ Why , In this way, the extremely large index value caused by large can be avoided . We will generate for each of the training set and the test set 100 Samples .

max_degree = 20  #  The maximum order of a polynomial 
n_train, n_test = 100, 100  #  Training and test data set size 
true_w = np.zeros(max_degree)  #  Allocate a lot of space 
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])

features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
    poly_features[:, i] /= math.gamma(i + 1)  # gamma(n)=(n-1)!
# labels Dimensions :(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)

Again , Stored in poly_features The monomial in consists of gamma Function to rescale , among $\Gamma (n)=(n-1)!$. Take a look at the previous... From the generated dataset 2 Samples , The first value is the constant characteristic corresponding to the offset .

# NumPy ndarray Convert to tensor
true_w, features, poly_features, labels = [torch.tensor(x, dtype=
    torch.float32) for x in [true_w, features, poly_features, labels]]

features[:2], poly_features[:2, :], labels[:2]

Train and test the model

Loss function

First, let's implement a function to evaluate the loss of the model on a given data set .

def evaluate_loss(net, data_iter, loss):  #@save
    """ Evaluate the loss of models on a given dataset """
    metric = d2l.Accumulator(2)  #  The sum of the losses , Number of samples 
    for X, y in data_iter:
        out = net(X)
        y = y.reshape(out.shape)
        l = loss(out, y)
        metric.add(l.sum(), l.numel())
    return metric[0] / metric[1]

Training functions

Now define the training function .

def train(train_features, test_features, train_labels, test_labels,
          num_epochs=400):
    loss = nn.MSELoss(reduction='none')
    input_shape = train_features.shape[-1]
    #  No offset is set , Because we've implemented it in polynomials 
    net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
    batch_size = min(10, train_labels.shape[0])
    train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
                                batch_size)
    test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
                               batch_size, is_train=False)
    trainer = torch.optim.SGD(net.parameters(), lr=0.01)
    animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
                            xlim=[1, num_epochs], ylim=[1e-3, 1e2],
                            legend=['train', 'test'])
    for epoch in range(num_epochs):
        d2l.train_epoch_ch3(net, train_iter, loss, trainer)
        if epoch == 0 or (epoch + 1) % 20 == 0:
            animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
                                     evaluate_loss(net, test_iter, loss)))
    print('weight:', net[0].weight.data.numpy())

Third order polynomial function fitting （ normal ）

We will first use third-order polynomial functions , It has the same order as the data generation function . It turns out that , The model can effectively reduce the training loss and test loss . The learned model parameters are also close to the real value $w=[5,1.2,-3.4,5.6]$.

#  Select the front from the polynomial features 4 Dimensions , namely 1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
      labels[:n_train], labels[n_train:])

weight: [[ 5.0008 1.2447366 -3.4524488 5.443078]]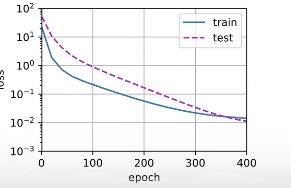

Linear function fitting （ Under fitting ）

Let's look at linear function fitting again , It is relatively difficult to reduce the training loss of the model . After the last iteration cycle , Training losses are still high . When used to fit nonlinear models （ Such as the third-order polynomial function here ） when , Linear models are prone to under fitting .

#  Select the front from the polynomial features 2 Dimensions , namely 1 and x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
      labels[:n_train], labels[n_train:])

weight: [[3.4807658 3.1861916]]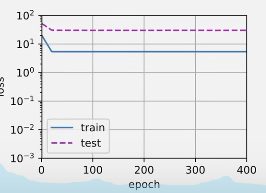

The losses haven't decreased at all

Higher order polynomial function fitting （ Over fitting ）

Now? , Let's try to train the model with a polynomial of too high order . under these circumstances , There is not enough data to learn that higher-order coefficients should have values close to zero . therefore , This overly complex model will be easily affected by the noise in the training data . Although the training loss can be effectively reduced , But the test loss is still high . It turns out that , Complex models over fit the data .

#  Select all dimensions from polynomial features 
train(poly_features[:n_train, :], poly_features[n_train:, :],
      labels[:n_train], labels[n_train:], num_epochs=1500)

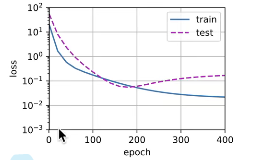
You can see the back W It should have been 0 Of , Are given values

QA

1. Data on time series , Training set and verification set may have autocorrelation , What should be done at this time ？
   Cut a piece , You can't take a piece from the middle

2. Are the model parameters different from the super parameters ？
   Model parameters refer to W and b
   Hyperparameters , For example, whether to choose linear model or multilayer perceptron . If it is a multi-layer perceptron , How many floors to choose , How big is each floor , What is the learning rate during training . Outside the model parameters , All we need to design , It's all super parameters .

3. How to effectively design super parameters , Can you only search ？ The best search method is Bayesian method or grid 、 Random ？
   The design of super parameters depends on your own experience .
   You can choose one model at a time , Then traverse the best one .