当前位置:网站首页>深度学习入门之线性代数(PyTorch)
深度学习入门之线性代数(PyTorch)
2022-07-03 09:27:00 【-素心向暖】
李沐老师学习笔记
线性代数

标量
简单操作
c = a + b
c = a·b
c = sin a
长度
∣ a ∣ = { a i f a > 0 − a o t h e r w i s e |a| = \begin{cases} a& ifa > 0 \\ -a& otherwise \end{cases} ∣a∣={ a−aifa>0otherwise
∣ a + b ∣ ≤ ∣ a ∣ + ∣ b ∣ |a+b|\le|a| + |b| ∣a+b∣≤∣a∣+∣b∣
∣ a ⋅ b ∣ = ∣ a ∣ ⋅ ∣ b ∣ |a·b|=|a|·|b| ∣a⋅b∣=∣a∣⋅∣b∣
向量
简单操作
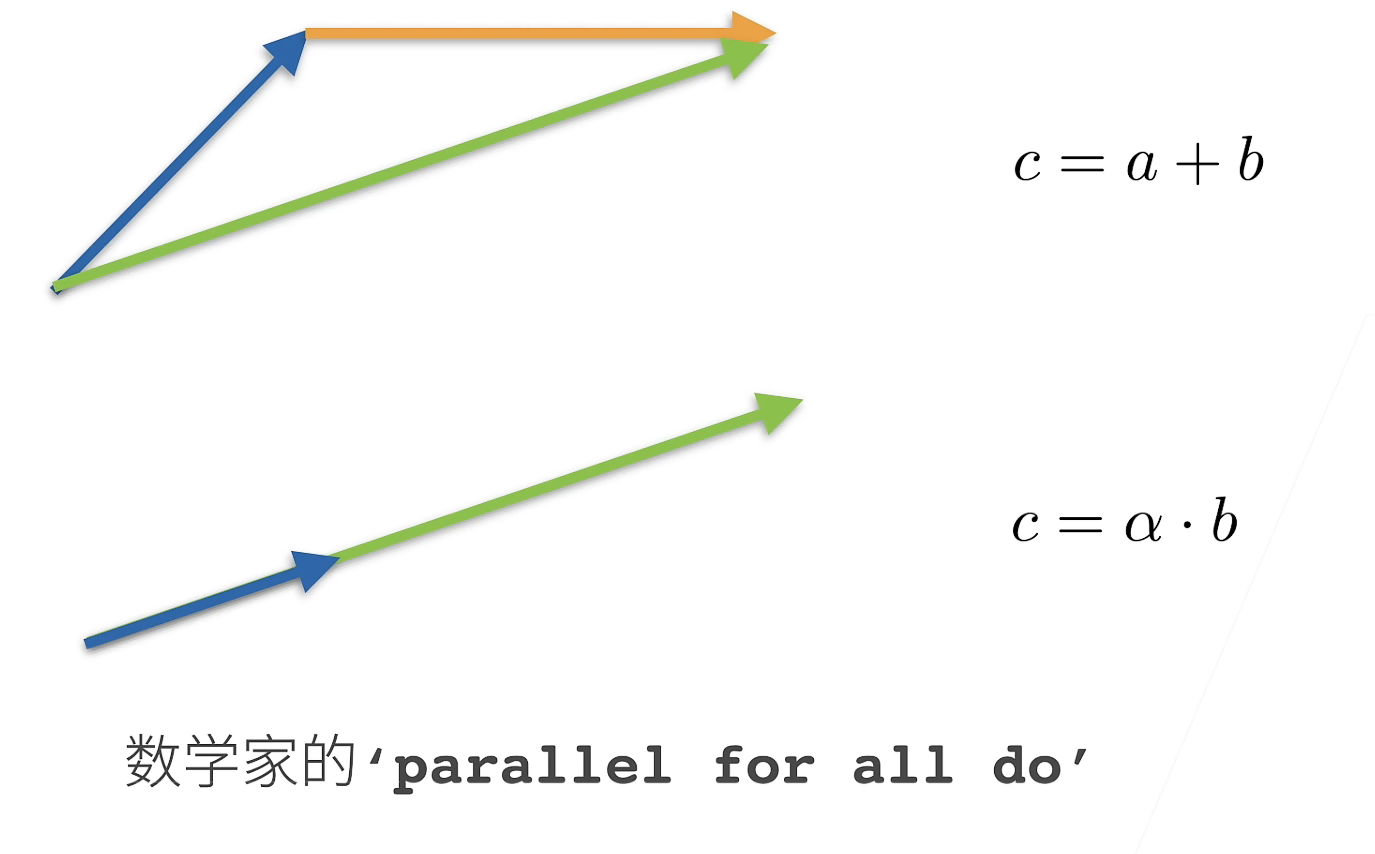
c = a + b w h e r e c i = a i + b i c=a+b\ \ \ where\ c_i=a_i+b_i c=a+b where ci=ai+bi
c = α ⋅ b w h e r e c i = α b i c=\alpha·b\ \ \ where\ c_i=\alpha b_i c=α⋅b where ci=αbi
c = s i n a w h e r e c i = s i n a i c=sina\ \ \ where\ c_i=sina_i c=sina where ci=sinai
长度
向量的长度,也就是向量的每个元素平方求和再开根号
∣ ∣ a ∣ ∣ 2 = [ ∑ i = 1 m a i 2 ] 1 2 ||a||_2=[\sum_{i=1}^ma_i^2]^{1 \over 2} ∣∣a∣∣2=[∑i=1mai2]21
∣ ∣ a ∣ ∣ ≥ 0 f o r a l l a ||a|| \ge 0\ for\ all\ a ∣∣a∣∣≥0 for all a
三角定理 ∣ ∣ a + b ∣ ∣ ≤ ∣ ∣ a ∣ ∣ + ∣ ∣ b ∣ ∣ ||a+b|| \le ||a|| + ||b|| ∣∣a+b∣∣≤∣∣a∣∣+∣∣b∣∣
如果 a 是一个常数的话 ∣ ∣ a ⋅ b ∣ ∣ = ∣ a ∣ ⋅ ∣ ∣ b ∣ ∣ ||a·b|| = |a|·||b|| ∣∣a⋅b∣∣=∣a∣⋅∣∣b∣∣
绿色是c
点乘
a T b = ∑ i a i b i a^Tb=\sum_ia_ib_i aTb=∑iaibi
正交
a T b = ∑ i a i b i = 0 a^Tb=\sum_ia_ib_i=0 aTb=∑iaibi=0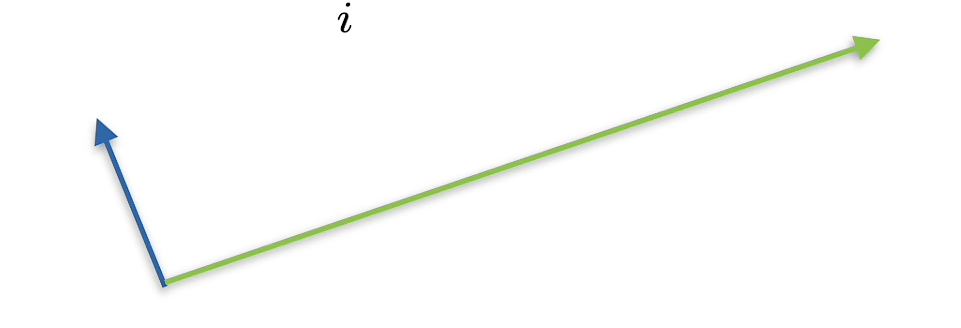
矩阵
简单操作

乘法(矩阵乘以向量)

乘法(矩阵乘以矩阵)
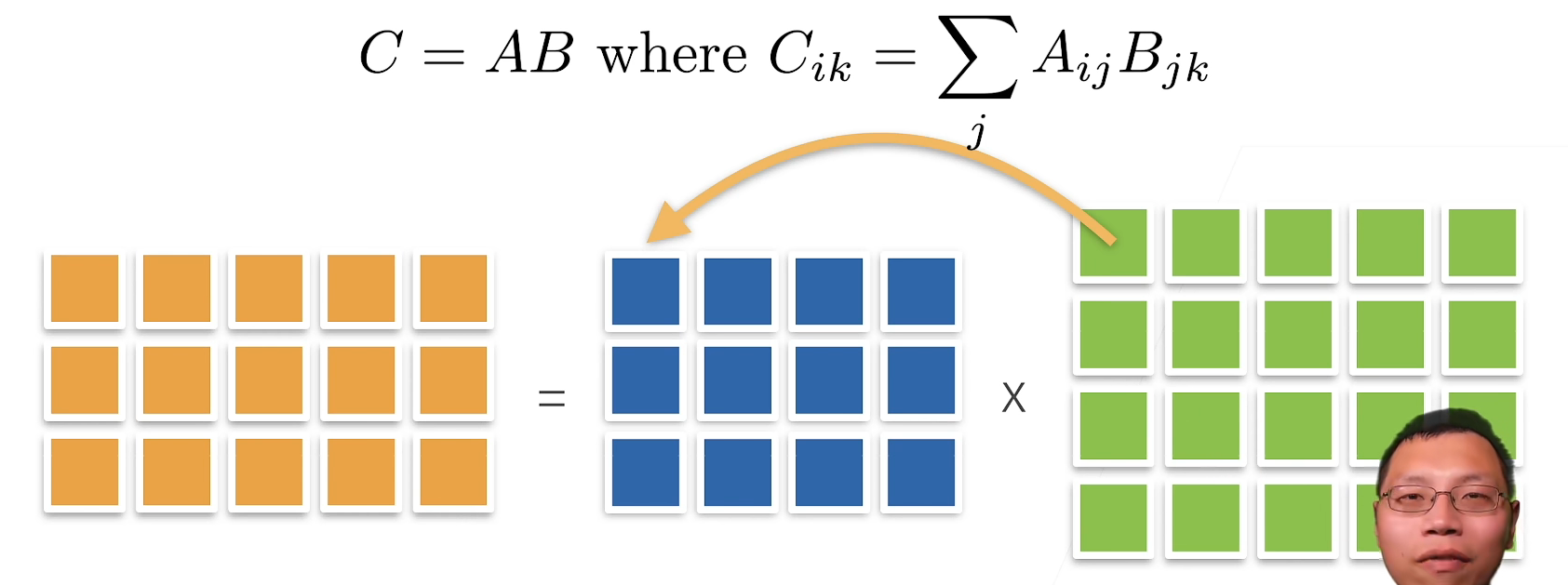
范数
c = A ⋅ b h e n c e ∣ ∣ c ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ⋅ ∣ ∣ b ∣ ∣ c=A·b\ hence\ ||c||\le||A||·||b|| c=A⋅b hence ∣∣c∣∣≤∣∣A∣∣⋅∣∣b∣∣
- 取决于如何衡量 b 和 c 的长度
- 常见范数
- 矩阵常数:最小的满足的上面公式的值
- Frobenius 范数
∣ ∣ A ∣ ∣ F r o b = [ ∑ i j A i j 2 ] 1 2 ||A||_{Frob}=[\sum_{ij}A^2_{ij}]^{1 \over 2} ∣∣A∣∣Frob=[ij∑Aij2]21
特殊矩阵
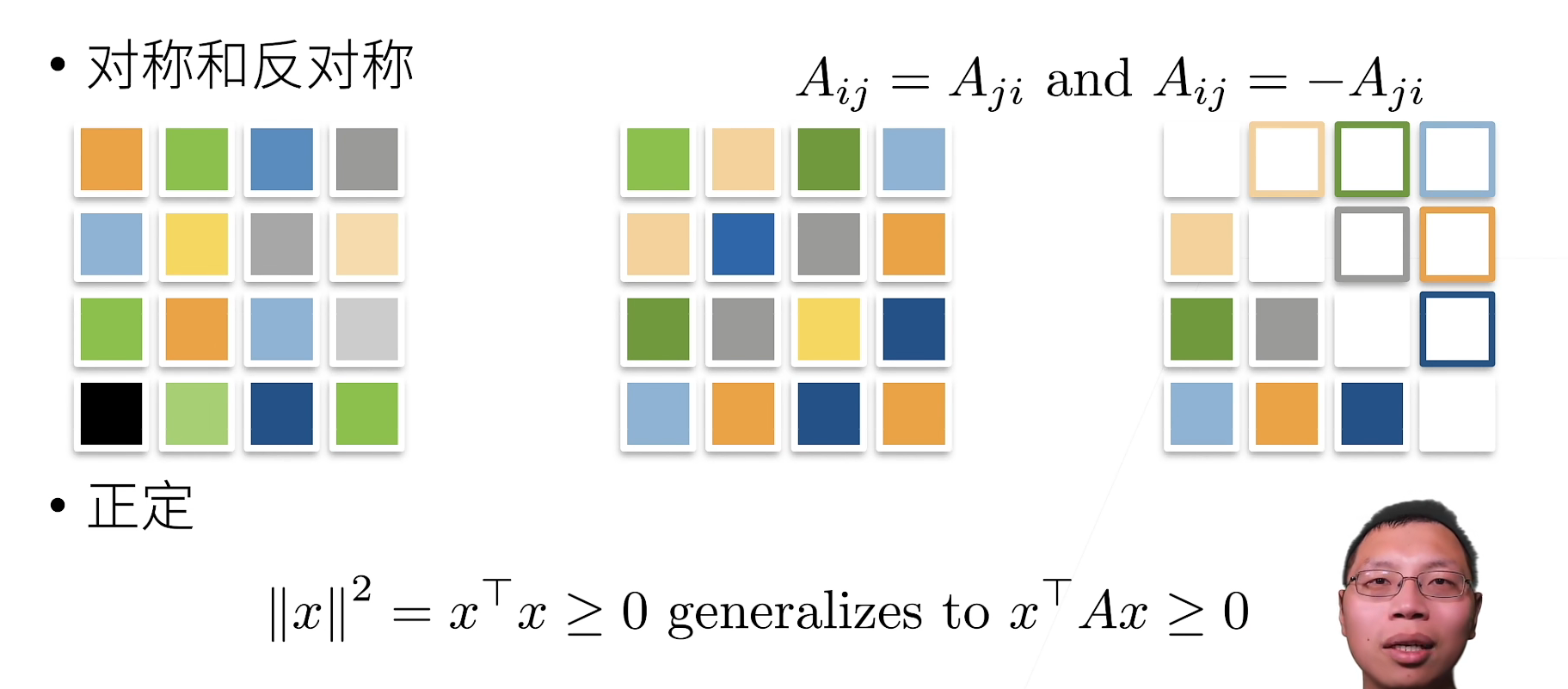
正交矩阵
所有行都相互正交
所有行都有单位长度 \qquad U w i t h ∑ j U i j U k j = δ i k U\ with \sum_jU_{ij}U_{kj}=\delta_{ik} U with∑jUijUkj=δik
可以写成 U U T = 1 UU^T=1 UUT=1置换矩阵
P w h e r e P i j = 1 i f a n d o n l y i f j = π ( i ) P\ where\ P_{ij}=1\ if\ and \ only\ if\ j=π(i) P where Pij=1 if and only if j=π(i)
置换矩阵是正交矩阵
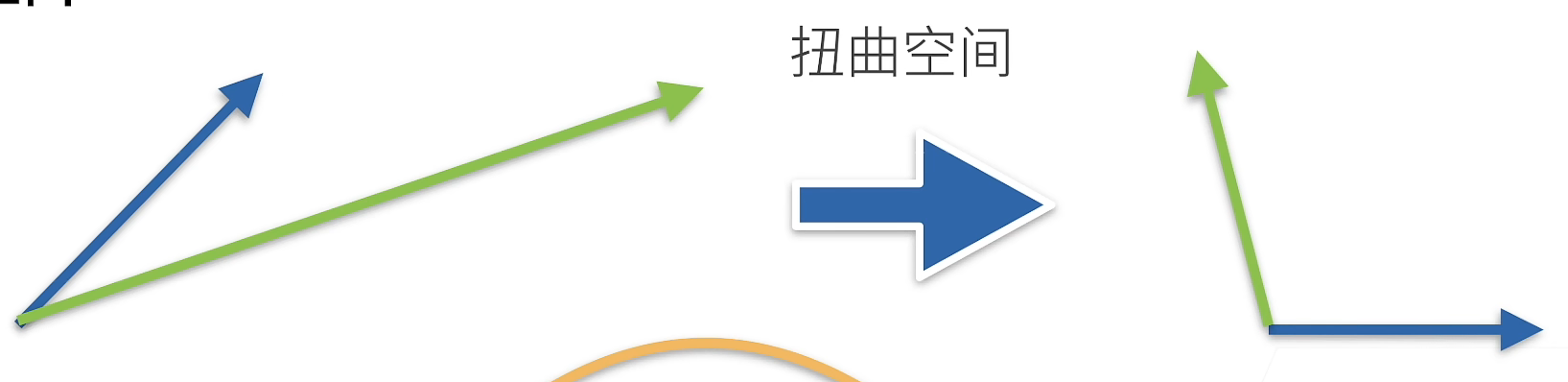
特征向量和特征值
矩阵就是将空间进行扭曲
- 不被矩阵改变方向的向量

- 对称矩阵总是可以找到特征向量
线性代数实现
标量
标量由只有一个元素的张量表示
import torch
x = torch.tensor([3.0])
y = torch.tensor([2.0])
x + y, x * y, x / y, x ** y
(tensor([5.]), tensor([6.]), tensor([1.5000]), tensor([9.]))
向量
你可以将向量视为标量组成的列表
x = torch.arange(4)
x
tensor([0, 1, 2, 3])
通过张量的索引来访问任一元素
x[3]
tensor(3)
index 都是从0开始的,数学的 index 是从1开始的
访问张量的长度
len(x)
4
只有一个轴的张量,性状只有一个元素
x.shape
torch.size([4])
矩阵
通过指定两个分量m和n来创建一个性状为m × n 的矩阵
A = torch.arange(20).reshape(5, 4)
A
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
矩阵的转置
A.T
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
对称矩阵(symmetric matrix)A 等于其转置: A = A T A=A^T A=AT
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
B
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
B == B.T
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
就像向量是标量的推广,矩阵就是向量的推广一样,我们可以构建具有更多轴的数据结构
X = torch.arange(24).reshape(2, 3, 4)
X
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
给定具有相同性状的任何两个张量,任何按元素二元结算的结构都将是相同性状的张量。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
A, A+B
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]]),
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]]))
两个矩阵的按元素乘法称为 哈达玛积(Hadamard product)(数学符号⊙)
A * B
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
a = 2
X =torch.arange(24).reshape(2, 3, 4)
a+X, (a*X).shape
(tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]]),
torch.Size([2, 3, 4]))
计算其元素的和
x = torch.arange(4, dtype=torch.float32)
x, x.sum()
(tensor([0., 1., 2., 3.]), tensor(6.))
指定求和汇总张量的轴
A = torch.arange(20*2).reshape(2, 5, 4)
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
(tensor([[20, 22, 24, 26],
[28, 30, 32, 34],
[36, 38, 40, 42],
[44, 46, 48, 50],
[52, 54, 56, 58]]),
torch.Size([5, 4]))
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
(tensor([[ 40, 45, 50, 55],
[140, 145, 150, 155]]),
torch.Size([2, 4]))
A.sum(axis=[0, 1, 2]) # Same as `A.sum()`
tensor(780)
可以理解为 axis=? ,就将那个维度处理掉
一个与求和相关的量是 平均值(mean或average)
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
A.mean(), A.sum() / A.numel()
(tensor(9.5000), tensor(9.5000))
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
(tensor([ 8., 9., 10., 11.]), tensor([ 8., 9., 10., 11.]))
计算总和或均值时保持轴数不变
sum_A = A.sum(axis=1, keepdims=True)
sum_A
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])

通过广播将A除以sum_A
A / sum_A
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
某个轴计算A元素的累计总和
A.cumsum(axis=0)
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
点积是相同位置的按元素乘积的和
y = torch.ones(4, dtype=torch.float32)
x, y, torch.dot(x, y)
(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))
我们可以通过执行按元素乘法,然后进行求和来表示两个向量的点积
torch.sum(x * y)
tensor(6.)
矩阵向量积Ax是一个长度为m的列向量,其 i t h i^{th} ith元素是点积 a i T x a_i^Tx aiTx
print(A)
print(x)
A.shape, x.shape, torch.mv(A, x)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([0., 1., 2., 3.])
(torch.Size([5, 4]), torch.Size([4]), tensor([ 14., 38., 62., 86., 110.]))
我们可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积,并将结果拼接在一起,形成 n X m 矩阵
B = torch.ones(4, 3)
torch.mm(A, B)
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
L 2 L_2 L2范数是向量元素平方和的平方根:
∣ ∣ x ∣ ∣ 2 = ∑ i = 1 n x i 2 ||x||_2= \sqrt{\sum_{i=1}^nx_i^2} ∣∣x∣∣2=i=1∑nxi2
u = torch.tensor([3.0, -4.0])
torch.norm(u)
tensor(5.)
范数 就是一个向量或者矩阵的长度
L 1 L_1 L1范数,它表示为向量元素的绝对值之和:
∣ ∣ x ∣ ∣ 1 = ∑ i = 1 n ∣ x i ∣ ||x||_1=\sum_{i=1}^n|x_i| ∣∣x∣∣1=i=1∑n∣xi∣
torch.abs(u).sum()
tensor(7.)
矩阵的弗罗贝尼乌斯范数(Frobenius norm) 是矩阵元素的平方和的平方根:
∣ ∣ X ∣ ∣ F = ∑ i = 1 m ∑ j = 1 n x i j 2 ||X||_F=\sqrt{\sum_{i=1}^m \sum_{j=1}^n x_{ij}^2} ∣∣X∣∣F=i=1∑mj=1∑nxij2
torch.norm(torch.ones((4, 9)))
tensor(6.)
等价于是把这个矩阵拉成一个向量,然后做向量的范数
QA
Q1:为什么机器学习要用张量来表示?
统计学较多使用张量来表示。
Q2:copy和clone的区别?
copy 可能不会复制内存,分浅拷贝和深拷贝
clone 必然会复制内存
Q3:torch不区分行向量和列向量?
如果想要区分行向量和列向量,需要使用矩阵。
如果用向量,向量对于计算机来说就是一个一维数组。
边栏推荐
- Leetcode-106: construct a binary tree according to the sequence of middle and later traversal
- Out of the box high color background system
- 20220605数学:两数相除
- Configure opencv in QT Creator
- Implementation of "quick start electronic" window dragging
- CV learning notes - BP neural network training example (including detailed calculation process and formula derivation)
- QT creator uses OpenCV Pro add
- SQL Server Management Studio cannot be opened
- Leetcode - the k-th element in 703 data flow (design priority queue)
- 20220601 Mathematics: zero after factorial
猜你喜欢

Secure in mysql8.0 under Windows_ file_ Priv is null solution
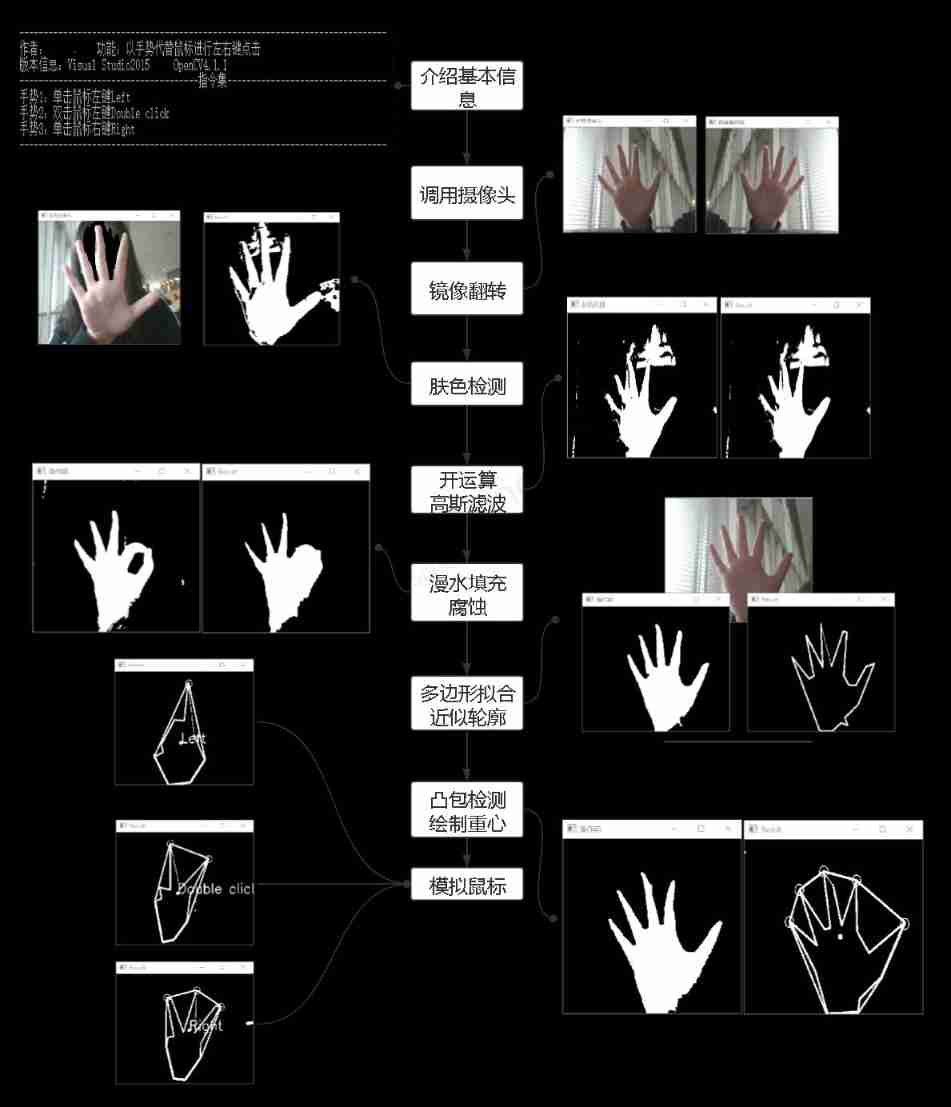
Simple real-time gesture recognition based on OpenCV (including code)
Data classification: support vector machine

Matplotlib drawing
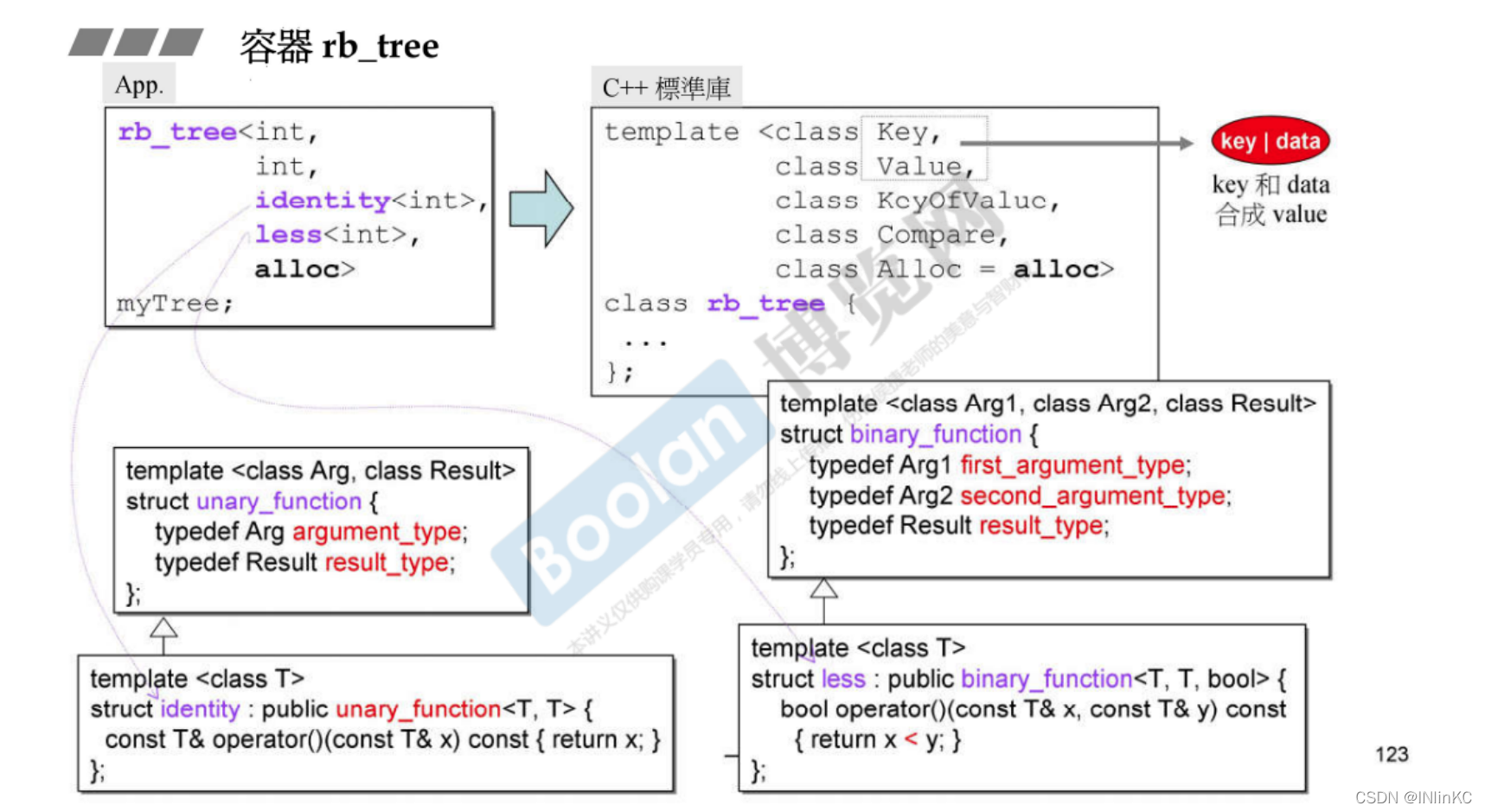
侯捷——STL源码剖析 笔记
Leetcode-112:路径总和

Hands on deep learning pytorch version exercise solution - 2.4 calculus

Leetcode-106:根据中后序遍历序列构造二叉树
一个30岁的测试员无比挣扎的故事,连躺平都是奢望

丢弃法Dropout(Pytorch)
随机推荐
1. Finite Markov Decision Process
Boston house price forecast (tensorflow2.9 practice)
Free online markdown to write a good resume
Leetcode刷题---278
Leetcode - the k-th element in 703 data flow (design priority queue)
20220605数学:两数相除
Yolov5 creates and trains its own data set to realize mask wearing detection
20220604数学:x的平方根
[graduation season] the picture is rich, and frugality is easy; Never forget chaos and danger in peace.
3.1 Monte Carlo Methods & case study: Blackjack of on-Policy Evaluation
【C 题集】of Ⅵ
20220531 Mathematics: Happy numbers
20220609其他:多数元素
Powshell's set location: unable to find a solution to the problem of accepting actual parameters
Deep learning by Pytorch
20220607 others: sum of two integers
Leetcode刷题---202
Flutter 退出当前操作二次确认怎么做才更优雅?
Leetcode刷题---374
Numpy Foundation