Machine learning theory learning: perceptron

perceptron (Perceptron) It's a two class linear classification model , The input is the eigenvector of the instance , The output is the category of the instance , take +1 and -1. The perceptron corresponds to the input space ( The feature space ) The instance is divided into positive and negative separated hyperplanes , It's a discriminant model . Perceptron prediction is to use the learned perceptron model to classify new input instances , It is the basis of neural network and support vector machine . The following reference links are highly recommended , It's very detailed .

Refer to the connection ：

machine learning —— perceptron

One 、 Perceptron model

Definition ： Input x, Corresponding to the feature points in the input space , Output y={+1,-1} Represents the category of the instance , The functions input to output are as follows ：
$$f(x)=sign(w\ast x+b)$$
It's called the perceptron .w、b Is the weight of the perceptron .

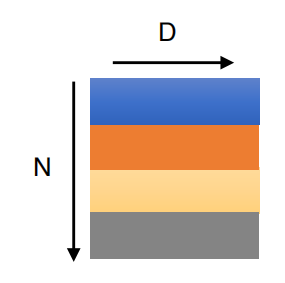
The perceptron is a linear classification model , It's a discriminant model . linear equation w*x+b=0 A hyperplane corresponding to the feature space S, This hyperplane divides the feature space into two parts , They are positive and negative .S Also called separating hyperplane , As shown in the figure below ：

Two 、 Perceptron learning strategies

Suppose the training data is linearly separable , The learning goal of the perceptron is to find a separation hyperplane that can completely separate the positive and negative samples , That is, to be sure w,b, It is necessary to define a loss function and minimize the loss function .

The perceptron selects the misclassification point to the separation hyperplane S The total distance as a loss function . input space $R^n$ Any point in $x_o$ The distance to the hyperplane ：
$$\frac{1}{||w||}|w\ast x_0+b|$$
among $||w||$ by w Of L2 norm .

【 Add 】

1、 The distance between a point and a line

Let the linear equation be Ax+By+C=0 , The last point is $(x_0,y_0)$, Then the distance is
$$d=\frac{A\ast x_0+B\ast y_0+C}{\sqrt{A^2+B^2}}$$
2、 Sample to hyperplane distance

Suppose the hyperplane is h=w⋅x+b, among w=(w0,w1,w2…wn), x=(x0,x1,x2…xn), Sample points x′ The distance to the hyperplane ：
$$d=\frac{w\ast x^{{}^{\prime }}+b}{||d||}$$

in addition , For misclassified classified data $(x_i,y_i)$ Come on , When $w\ast x_i+b>0$ when ,$y_i=-1$; And when $w\ast x_i+b<0$ when ,$y_i=+1$. therefore , Misclassification to S The distance to ：
$$-\frac{1}{||w||}{y}_i(w\ast x_i+b)$$
Don't consider $\frac{1}{||w||}$, The loss function of the perceptron is defined as ：
$$L(w,b)=-\sum y_i(w\ast x_i+b)$$

3、 ... and 、 Perceptron learning algorithm

3.1、 The original form of Perceptron Algorithm

For a given data set $T=(x_1,y_1),...,(x_N,y_N)$ Find parameters w,b Minimize the loss function ：
$$minL(w,b)=-\sum y_i(w\ast x_i+b)$$
Because we need to keep learning w,b, Therefore, we adopt the random gradient descent method to continuously optimize the objective function , ad locum , In the process of random gradient descent , Each time, only one misclassification point sample is used to reduce its gradient .

First , We solve the gradient , Respectively for w,bw,b Finding partial derivatives :
$$\begin{gathered} \nabla wL(w,b)=\frac{\partial }{\partial w}L(w,b)=-\sum yixi \\ \nabla bL(w,b)=\frac{\partial }{\partial b}L(w,b)=-\sum yi \end{gathered}$$
then , Randomly select a misclassification point pair w,bw,b updated ： ( Synchronize updates )
$$\begin{gathered} w\leftarrow w+\eta yixi \\ b\leftarrow b+\eta yi \end{gathered}$$

among ,η For learning rate , Through this iteration, the loss function L(w,b) Constantly decreasing , Until minimized .

Algorithm steps ：

Input ：$T=(x_1,y_1),...,(x_N,y_N)$, Learning rate η(0<η<=1)

Output ：w,b; Perceptron model $f(x)=sign(w\ast x+b)$

1. Select the initial value $w_0,b_0$
2. Select data $(x_i,y_i)$
3. If $y_i(w\ast x_i+b)<=0$

$$\begin{gathered} w\leftarrow w+\eta yixi \\ b\leftarrow b+\eta yi \end{gathered}$$

4. Transferred to （2）, There are no misclassification points until the training set

According to the algorithm, we can see , Perceptron mainly uses misclassification points to learn , Through adjustment w,b Value , Move the separation hyperplane to the misclassification point , Reduce the distance from the separation point to the plane , Until the hyperplane crosses the point so that it is correctly classified .

3.2、 Dual form of Perceptron Algorithm

We know the general form of weight update ：
$$\begin{gathered} w\leftarrow w+\eta yixi \\ b\leftarrow b+\eta yi \end{gathered}$$
But after many iterations , We need to update many times w、b The weight , This calculation is relatively large . Is there a way to calculate the weight without so many times ? Yes , That is the dual form of Perceptron Algorithm . Specifically, how to lead out can ？ We know what happened n After modification , The parameter changes are as follows ：
$$\begin{gathered} w=\sum _i{a}_i{y}_i{x}_i \\ b=\sum _i{a}_i{y}_i \end{gathered}$$
among $a_i$ It is a misclassification point $(x_i,y_i)$ Number of updates required

So we can learn from w,b Become the number of learning misclassification $a_i$, And in the dual form Gram Matrix to store the inner product , It can improve the operation speed , In contrast to the original form , Every time the parameters change , All matrix calculations need to be calculated , This leads to a much larger amount of computation than the dual form , This is the efficiency of the dual form . here Gram The matrix is equivalent to ${\sum }_i{y}_i{x}_i$.Gram The definition of a matrix is as follows ：
$$G=\left[\begin{array}{ccc}{x}_1{x}_1& ...& x_1{x}_N\\ x_2{x}_1& ...& x_2{x}_N\\ ...& ...& ...\\ x_N{x}_1& ...& x_N{x}_N\end{array}\right]$$
Algorithm steps ：

Input ：$T=(x_1,y_1),...,(x_N,y_N)$, Learning rate η(0<η<=1)

Output ：a,b; Perceptron model $f(x)=sign({\sum }_j{a}_j{y}_i{x}_j\ast x_i+b)$

1. Assign initial value to a0,b0 .
2. Select data points (xi,yi).
3. Judge whether the data point is the misclassification point of the current model , That is, judge if $y_i({\sum }_j{a}_j{y}_j{x}_j\ast x_i+b)<=0$ Update

$$\begin{gathered} a_i=a_i+\eta \\ b=b+\eta y_i \end{gathered}$$

4. go to （2）, Until there are no misclassification points in the training set

In order to reduce the amount of calculation , We can calculate the inner product in the formula in advance , obtain Gram matrix .

Refer to the connection ：

Introduction to machine learning 《 Statistical learning method 》 Take notes —— perceptron