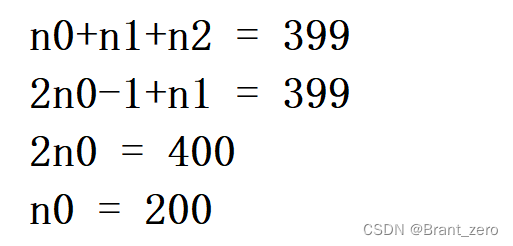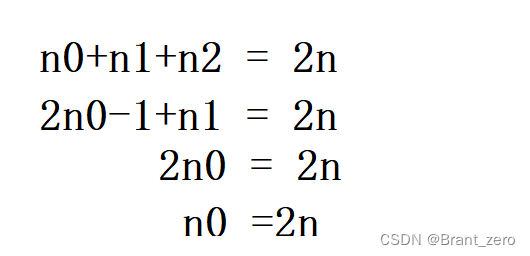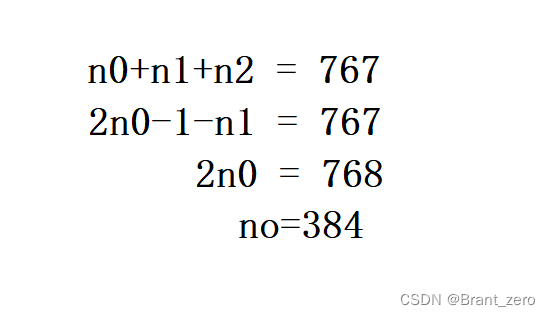当前位置:网站首页>二叉树的基本概念和性质
二叉树的基本概念和性质
2022-07-07 16:50:00 【Brant_zero】
目录
1.3 树的表示
一、树的概念和结构
1.1 树的概念
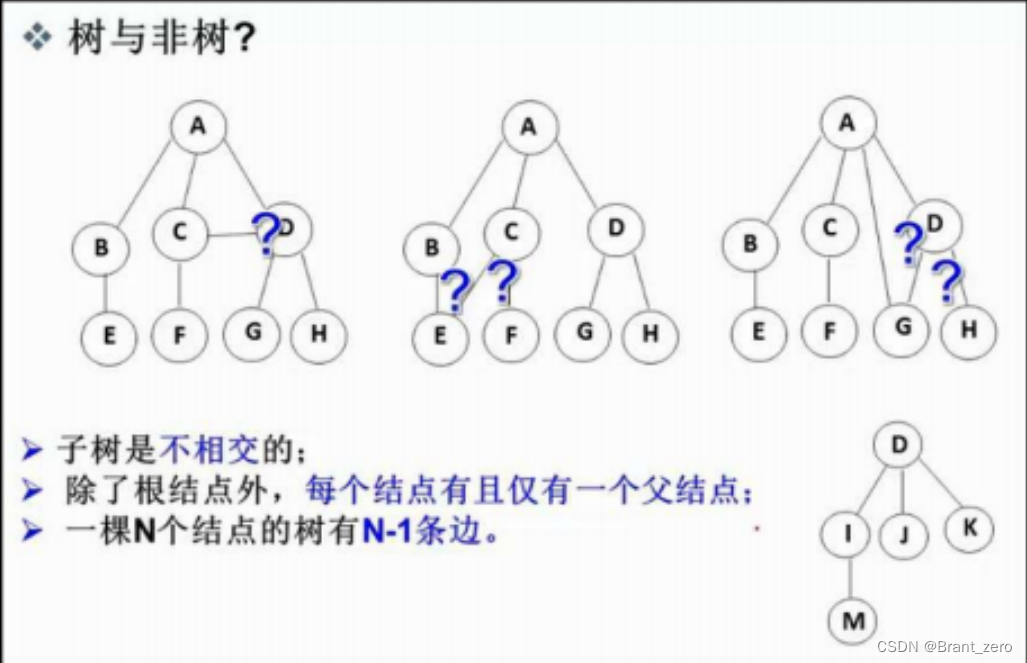
树是一种非线性的数据结构,他是由n(n>=0)个有限结点组成的一个具有层次关系的集合。叫做树是因为其结构像一颗倒挂的树,即根朝上,而叶朝下。
- 有一个特殊的节点,称为根节点,根结点没有前驱结点。
- 除了根节点,其余结点被分成M(M>0)个互不相交的集合T1、T2……Tn,其中每一个集合Ti(1 <= i <= n)又是一颗树结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继结点。
- 因此,树是递归定义的。
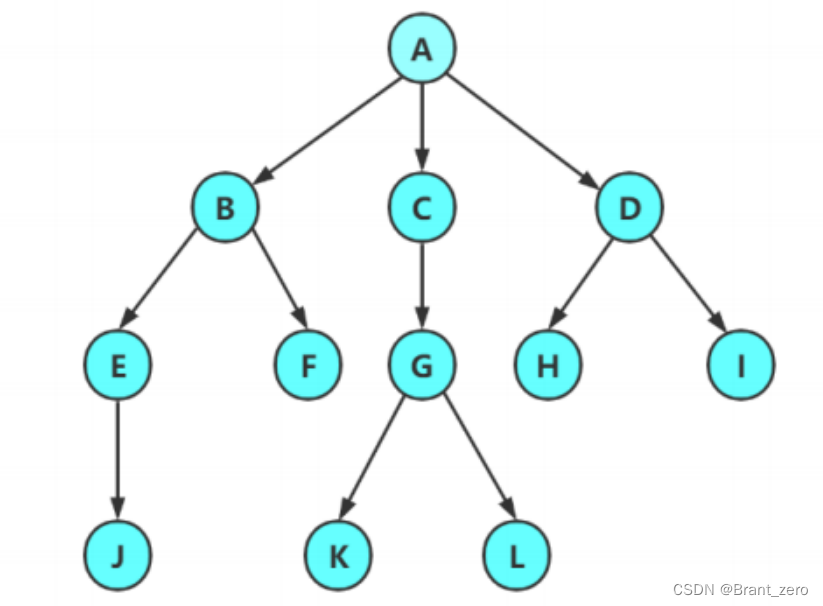
注意:树形结构中,子树之间不能有交集,否则就不是树形结构,而应是图型的数据结构。
1.2 树的重要概念
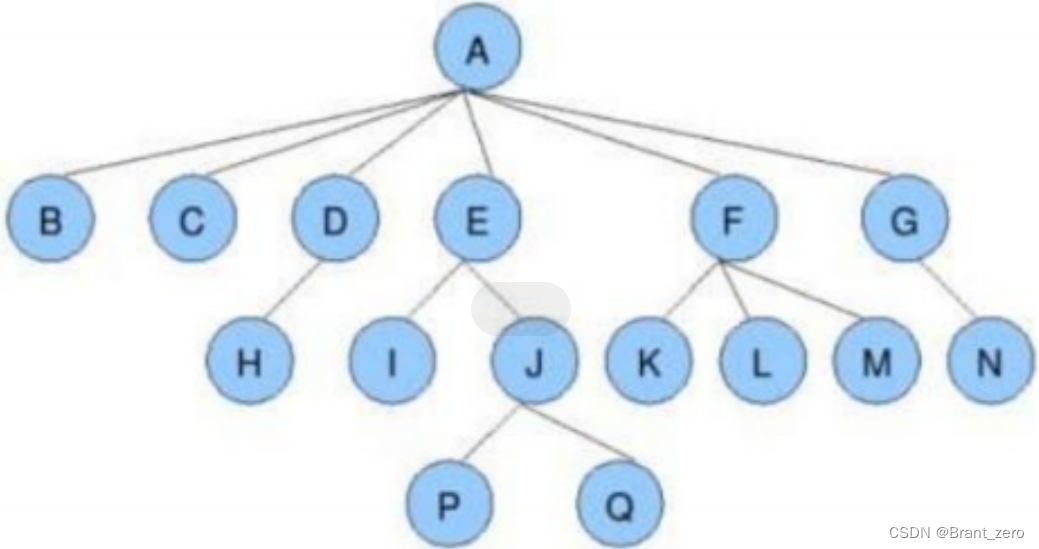
重要:
节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的度为6。
叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I……等为叶节点。
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点。
孩子节点或子节点:一个节点含有的子树的根节点称为节点的子节点;如上图:B是A的孩子节点。
树的高度或深度:树种节点的最大层次;如上图:树的高度为4。
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先。
子孙:从某节点为根的子树种任一节点都称之为该节点的子孙。如上图:所有节点都是A的子孙。
树的度:一颗树中,最大节点的度称之为树的度;如上图:树的度为6。
其次:
非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G……等节点为分支节点。
兄弟节点:具有相同父节点的节点称为兄弟节点;如上图:B、C是兄弟节点。
节点的层次:从根开始定义起,根为第一层,根的子节点为第二层,以此类推;
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为堂兄弟节点。
森林:由m(M>0)棵互不相交的树的集合称为森林。
1.3 树的表示
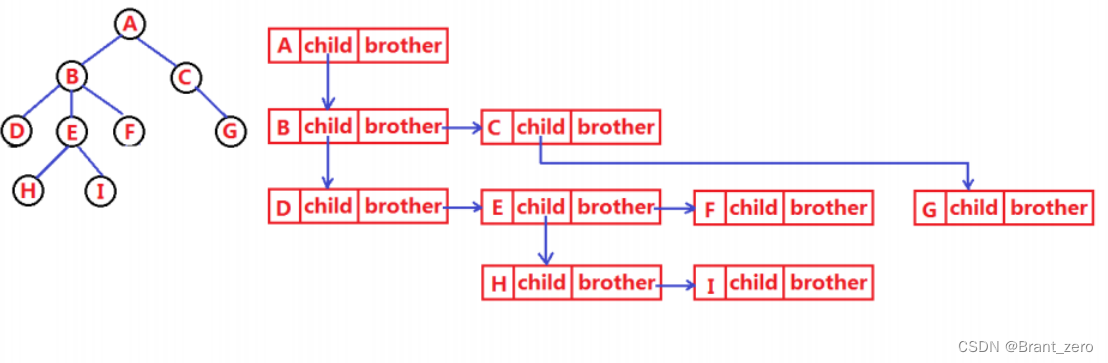
树结构相对于线性表就比较复杂了,既要保存值域、也要保存结点和结点之间的关系,实际中树有很多种表示方法,这里了解一下最常用的孩子兄弟表示法即可。
typedef int DataType;
struct Node
{
struct Node* firstChild1; // 第一个孩子结点
struct Node* pNextBrother; // 指向其下一个兄弟结点
DataType data; // 结点中的数据域
};二、 二叉树概念及结构
2.1 二叉树的概念
一颗二叉树是结点的一个有限集合,该集合:
- 或则为空
- 由一个根结点加上两棵别称为左子树和右子树的二叉树组成。
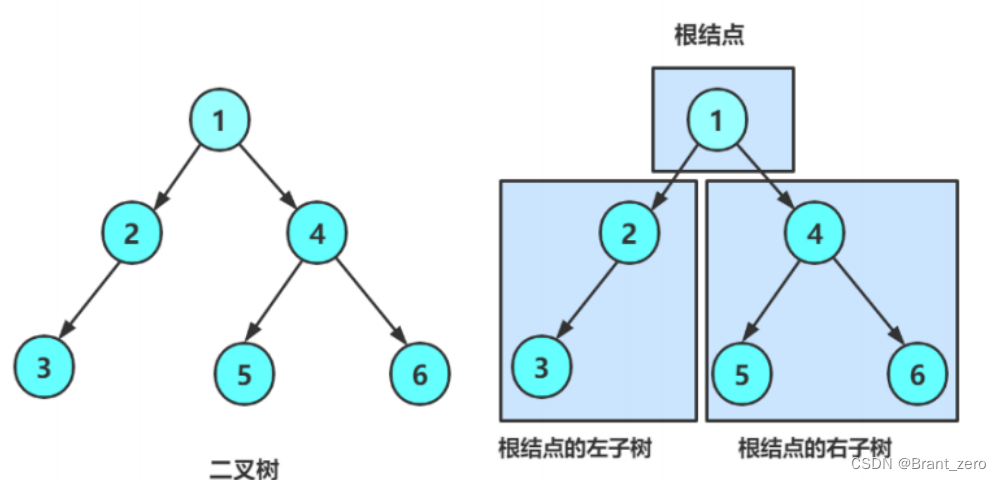
从上图可以看出:
- 二叉树不存在度大于2的结点。
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树。
2.2 特殊的二叉树
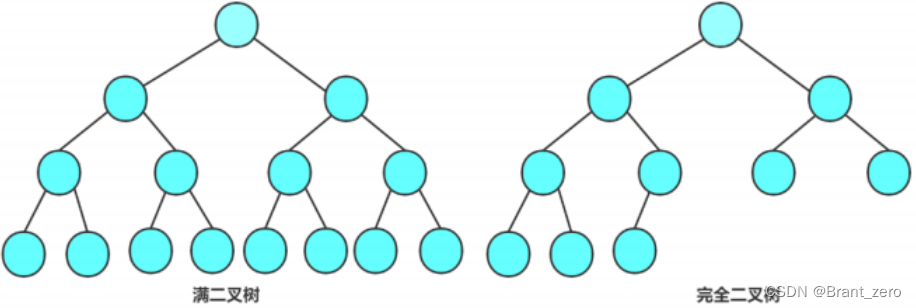
- 满二叉树:一个二叉树,如果每一层的结点树都达到最大值,啧啧换个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是
-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据机构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有N个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点——对应时称为完全二叉树。(第n层不满但是从左到右为连续,n-1层全满),要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
重要:
- 若规定根结点的层数为1,则一颗非空二叉树的第i层上最多有
个结点。
- 若规定根结点的层数为1,则深度为h的二叉树的最大节点是
.
- 对任何一颗二叉树,如果度为0其叶节点个数为n0,
- 若规定根节点的层数为1,具有n的结点的满二叉树的深度,
.
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置节点的双亲序号:(i-1)/2; i=0, i为根结点编号,无双亲结点
- 若2i+1<n , 左孩子序号:2i+1, 2i+1>=n否则无左孩子
- 若2i+2<n , 右孩子序号:2i+2,2i+2>=n 否则无右孩子
2.4 二叉树练习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为 ()A 不存在这样的二叉树B 200C 198D 199
2.下列数据结构中,不适合采用顺序存储结构的是 ()A 非完全二叉树B 堆C 队列D 栈
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为 ()A nB n+1C n-1D n/2
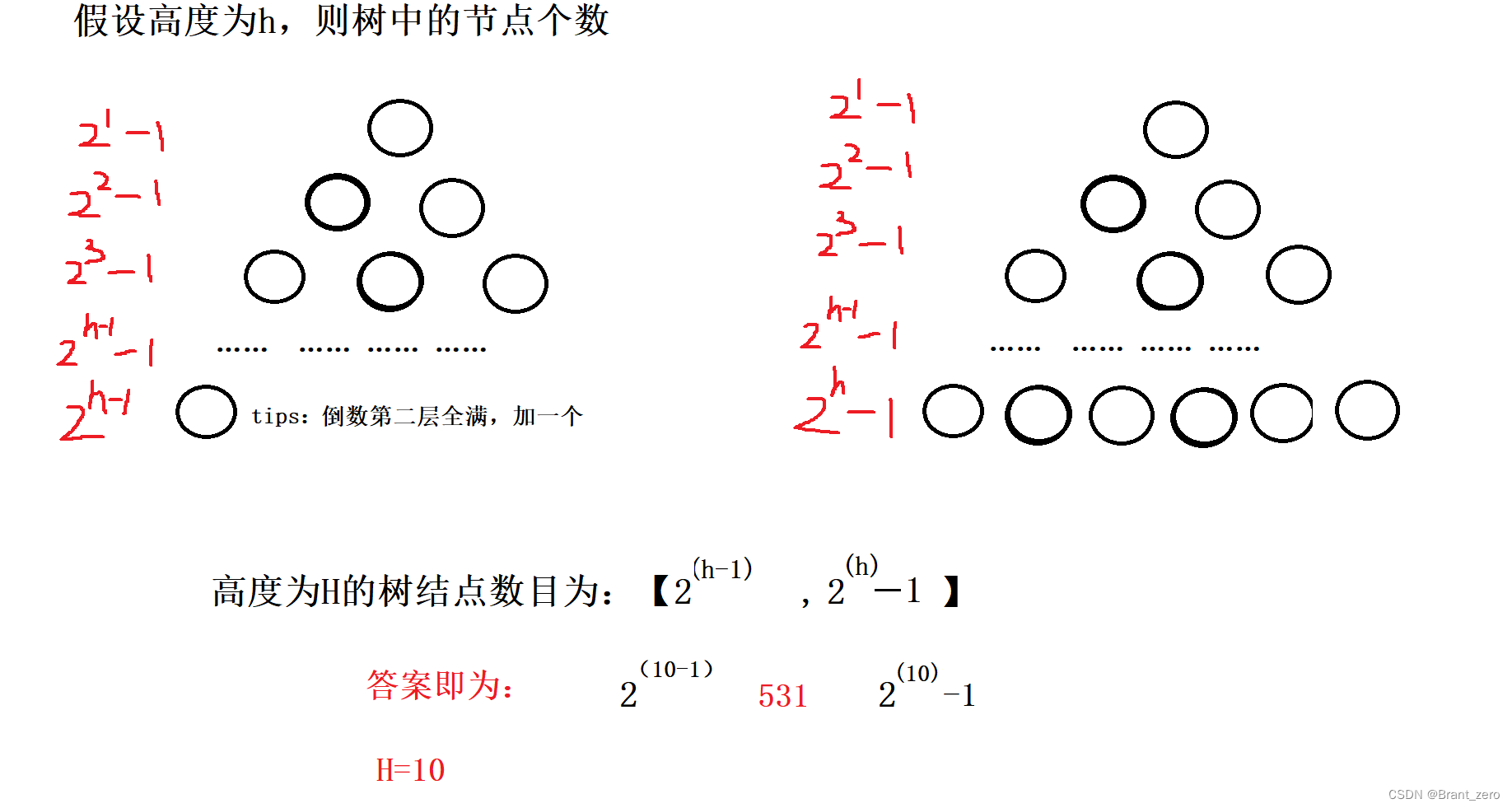
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为 ()A 11B 10C 8D 12
5.一个具有767个节点的完全二叉树,其叶子节点个数为()A 383B 384C 385D 386
答案:
第一题:
第二题: B
第三题:
第四题:
第五题:
本篇到此就结束了,其中重点在于树的概念和二叉树的性质,这些是理解二叉树的精髓,也是考试的出题点,希望大家可以理解。
下篇博客会带来链式二叉树的基本结构和功能,希望大家持续关注。
边栏推荐
- 企业展厅设计中常用的三种多媒体技术形式
- [principles and technologies of network attack and Defense] Chapter 3: network reconnaissance technology
- AntiSamy:防 XSS 攻击的一种解决方案使用教程
- 面试唯品会实习测试岗、抖音实习测试岗【真实投稿】
- Tips for this week 140: constants: safety idioms
- Unlike the relatively short-lived industrial chain of consumer Internet, the industrial chain of industrial Internet is quite long
- Save the memory of the model! Meta & UC Berkeley proposed memvit. The modeling time support is 30 times longer than the existing model, and the calculation amount is only increased by 4.5%
- debian10编译安装mysql
- socket编程之常用api介绍与socket、select、poll、epoll高并发服务器模型代码实现
- Tsinghua, Cambridge and UIC jointly launched the first Chinese fact verification data set: evidence-based, covering many fields such as medical society
猜你喜欢
Hash, bitmap and bloom filter for mass data De duplication
![[paper sharing] where's crypto?](/img/27/9b47bfcdff8307e63f2699d6a4e1b4.png)
[paper sharing] where's crypto?
Discuss | frankly, why is it difficult to implement industrial AR applications?

More than 10000 units were offline within ten days of listing, and the strength of Auchan Z6 products was highly praised
Year SQL audit platform
Debian10 compile and install MySQL
![[principles and technologies of network attack and Defense] Chapter 5: denial of service attack](/img/18/ac8b4c0dba4dd972df119d2f670416.png)
[principles and technologies of network attack and Defense] Chapter 5: denial of service attack
![学习open62541 --- [67] 添加自定义Enum并显示名字](/img/98/e5e25af90b3f98c2be11d7d21e5ea6.png)
学习open62541 --- [67] 添加自定义Enum并显示名字
debian10系统问题总结
C语言中匿名的最高境界
随机推荐
Tips of the week 136: unordered containers
持续测试(CT)实战经验分享
[paddleseg source code reading] add boundary IOU calculation in paddleseg validation (1) -- val.py file details tips
回归测试的分类
SQLite SQL exception near "with": syntax error
【软件测试】从企业版BOSS直聘,看求职简历,你没被面上是有原因的
小程序中实现付款功能
Discuss | frankly, why is it difficult to implement industrial AR applications?
回归问题的评价指标和重要知识点总结
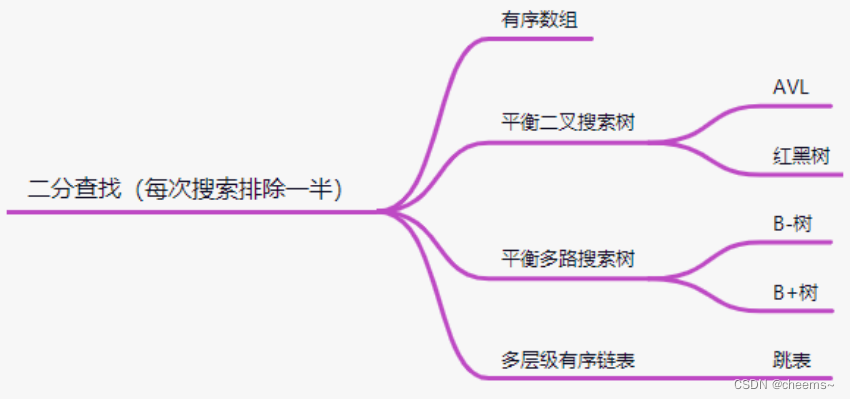
Hash, bitmap and bloom filter for mass data De duplication
Rules for filling in volunteers for college entrance examination
Performance test process and plan
Tips of this week 141: pay attention to implicit conversion to bool
CVPR 2022丨学习用于小样本语义分割的非目标知识
Nunjuks template engine
同消费互联网的较为短暂的产业链不同,产业互联网的产业链是相当漫长的
Live broadcast software construction, canvas Text Bold
idea彻底卸载安装及配置笔记
[principle and technology of network attack and Defense] Chapter 1: Introduction
AntiSamy:防 XSS 攻击的一种解决方案使用教程
 -1,则它就是满二叉树。
-1,则它就是满二叉树。 个结点。
个结点。 .
. .
.