当前位置:网站首页>自适应控制——仿真实验三 用超稳定性理论设计模型参考自适应系统
自适应控制——仿真实验三 用超稳定性理论设计模型参考自适应系统
2022-07-31 14:28:00 【lan 606】
一、问题描述
设控制对象的传递函数为
W p ( s ) = k 1 T 1 2 s 2 + 2 T 1 ξ 1 s + 1 (1) W_{p}(s)=\frac{k_{1}}{T_{1}^{2} s^{2}+2 T_{1} \xi_{1} s+1} \tag{1} Wp(s)=T12s2+2T1ξ1s+1k1(1)
参数 k 1 k_1 k1, T 1 T_{1} T1 和 ξ 1 \xi_{1} ξ1 随时间而变的变化规律为
k 1 ( t ) = 1.12 − 0.008 t , T 1 ( t ) = 0.036 + 0.004 t , ξ 1 ( t ) = 0.8 − 0.01 t (2) k_{1}(t)=1.12-0.008 t, \quad T_{1}(t)=0.036+0.004 t, \quad \xi_{1}(t)=0.8-0.01 t \tag{2} k1(t)=1.12−0.008t,T1(t)=0.036+0.004t,ξ1(t)=0.8−0.01t(2)
设参考模型的传递函数为
W m ( s ) = 1 0.0 8 2 s 2 + 2 × 0.08 × 0.75 s + 1 (3) W_{m}(s)=\frac{1}{0.08^{2} s^{2}+2 \times 0.08 \times 0.75 s+1} \tag{3} Wm(s)=0.082s2+2×0.08×0.75s+11(3)
用超稳定性理论设计模型参考自适应系统。
假定系统参考输入:
r ( t ) r(t) r(t) 是方波信号,周期为4s,振幅为 ± 2 \pm 2 ±2。
设计自适应规律,给出仿真结果。
二、问题建模
本次仿真实验主要针对的是带状态变量滤波器(情况1)下的并联模型参考自适应控制系统。设参考模型方程为:
( ∑ i = 0 n a m i p i ) y m = ( ∑ i = 0 m b m i p i ) r , a m n = 1 (4) \left(\sum_{i=0}^{n} a_{m i} p^{i}\right) y_{m}=\left(\sum_{i=0}^{m} b_{m i} p^{i}\right) r, a_{m n}=1 \tag{4} (i=0∑namipi)ym=(i=0∑mbmipi)r,amn=1(4)
接在参考模型输出端的状态变量滤波器的方程为:
( ∑ i = 0 n − 1 c i p i ) y m f = y m , c n − 1 = 1 (5) \left(\sum_{i=0}^{n-1} c_{i} p^{i}\right) y_{m f}=y_{m}, c_{n-1}=1 \tag{5} (i=0∑n−1cipi)ymf=ym,cn−1=1(5)
接在可调系统输入端的状态变量滤波器的方程为:
( ∑ i = 0 n − 1 c i p i ) r f = r , c n − 1 = 1 (6) \left(\sum_{i=0}^{n-1} c_{i} p^{i}\right) r_{f}=r, c_{n-1}=1 \tag{6} (i=0∑n−1cipi)rf=r,cn−1=1(6)
可调系统方程为:
( ∑ i = 0 n a s i ( v , t ) p i ) y s f = ( ∑ i = 0 m b s i ( v , t ) p i ) r f , a s n ( v , t ) = 1 (7) \left(\sum_{i=0}^{n} a_{s i}(v, t) p^{i}\right) y_{s f}=\left(\sum_{i=0}^{m} b_{s i}(v, t) p^{i}\right) r_{f}, a_{s n}(v, t)=1 \tag{7} (i=0∑nasi(v,t)pi)ysf=(i=0∑mbsi(v,t)pi)rf,asn(v,t)=1(7)
广义输出误差为:
ε f = y m f − y s f (8) \varepsilon_{f}=y_{m f}-y_{s f} \tag{8} εf=ymf−ysf(8)
为保证等价的前向方块严格正实,引入串联补偿器:
v = D ( p ) ε f = ( ∑ i = 0 n − 1 d i p i ) ε f (9) v=D(p) \varepsilon_{f}=\left(\sum_{i=0}^{n-1} d_{i} p^{i}\right) \varepsilon_{f} \tag{9} v=D(p)εf=(i=0∑n−1dipi)εf(9)
对于可调系统中的可调参数 a s i ( v , t ) a_{si}(v,t) asi(v,t) 及 b s i ( v , t ) b_{si}(v,t) bsi(v,t),采取PI控制,则自适应规律为
a s i ( v , t ) = ∫ 0 t φ 1 i ( v , t , τ ) d τ + φ 2 i ( v , t ) + a s i ( 0 ) , i = 0 , 1 , ⋯ , n − 1 b s i ( v , t ) = ∫ 0 t ψ 1 i ( v , t , τ ) d τ + ψ 2 i ( v , t ) + b s i ( 0 ) , i = 0 , 1 , ⋯ , m (10) \begin{aligned} a_{s i}(v, t)&=\int_{0}^{t} \varphi_{1 i}(v, t, \tau) d \tau+\varphi_{2 i}(v, t)+a_{s i}(0), i=0,1, \cdots, n-1 \\ b_{s i}(v, t)&=\int_{0}^{t} \psi_{1 i}(v, t, \tau) d \tau+\psi_{2 i}(v, t)+b_{s i}(0), i=0,1, \cdots, m \end{aligned} \tag{10} asi(v,t)bsi(v,t)=∫0tφ1i(v,t,τ)dτ+φ2i(v,t)+asi(0),i=0,1,⋯,n−1=∫0tψ1i(v,t,τ)dτ+ψ2i(v,t)+bsi(0),i=0,1,⋯,m(10)
将参考模型与状态变量滤波器互换位置,可得到形式同(7)式的参考模型方程如下:
( ∑ i = 0 n a m i p i ) y m f = ( ∑ i = 0 m b m i p i ) r f , a m n = 1 (11) \left(\sum_{i=0}^{n} a_{m i} p^{i}\right) y_{m f}=\left(\sum_{i=0}^{m} b_{m i} p^{i}\right) r_{f}, a_{m n}=1 \tag{11} (i=0∑namipi)ymf=(i=0∑mbmipi)rf,amn=1(11)
结合(7)式,(11)式和(8)式,可推导出
( ∑ i = 0 n a m i p i ) ε f = [ ∑ i = 0 n ( a s i − a m i ) p i ] y s f + [ ∑ i = 0 n ( b m i − b s i ) p i ] r f (12) \left(\sum_{i=0}^{n} a_{m i} p^{i}\right) \varepsilon_{f}=\left[\sum_{i=0}^{n}\left(a_{s i}-a_{m i}\right) p^{i}\right] y_{s f}+\left[\sum_{i=0}^{n}\left(b_{m i}-b_{s i}\right) p^{i}\right] r_{f} \tag{12} (i=0∑namipi)εf=[i=0∑n(asi−ami)pi]ysf+[i=0∑n(bmi−bsi)pi]rf(12)
令
ω 1 = [ ∑ i = 0 n ( a s i − a m i ) p i ] y s f + [ ∑ i = 0 n ( b m i − b s i ) p i ] r f (13) \omega_{1}=\left[\sum_{i=0}^{n}\left(a_{s i}-a_{m i}\right) p^{i}\right] y_{s f}+\left[\sum_{i=0}^{n}\left(b_{m i}-b_{s i}\right) p^{i}\right] r_{f} \tag{13} ω1=[i=0∑n(asi−ami)pi]ysf+[i=0∑n(bmi−bsi)pi]rf(13)
则(12)式变成
( ∑ i = 0 n a m i p i ) ε f = ω 13 (14) \left(\sum_{i=0}^{n} a_{m i} p^{i}\right) \varepsilon_{f}=\omega_{13} \tag{14} (i=0∑namipi)εf=ω13(14)
将可调系统中的可调参数选定的自适应规律(10)式代入(13)式中,可得反馈方框的输出量 ω \omega ω 的形式如下:
ω = − ω 1 = − { ∑ i = 0 n − 1 [ ∫ 0 t φ 1 i ( v , t , τ ) d τ + φ 2 i ( v , t ) + a s i ( 0 ) − a m i ] p i } y s f + { ∑ i = 0 n − 1 [ ∫ 0 t ψ 1 i ( v , t , τ ) d τ + ψ 2 i ( v , t ) + b s i ( 0 ) − b m i ] p i } r f (15) \begin{aligned} \omega=-\omega_{1}=&-\left\{\sum_{i=0}^{n-1}\right. {\left.\left[\int_{0}^{t} \varphi_{1 i}(v, t, \tau) d \tau+\varphi_{2 i}(v, t)+a_{s i}(0)-a_{m i}\right] p^{i}\right\} y_{s f} } \\ &+\left\{\sum_{i=0}^{n-1}\left[\int_{0}^{t} \psi_{1 i}(v, t, \tau) d \tau+\psi_{2 i}(v, t)+b_{s i}(0)-b_{m i}\right] p^{i}\right\} r_{f} \end{aligned} \tag{15} ω=−ω1=−{ i=0∑n−1[∫0tφ1i(v,t,τ)dτ+φ2i(v,t)+asi(0)−ami]pi}ysf+{ i=0∑n−1[∫0tψ1i(v,t,τ)dτ+ψ2i(v,t)+bsi(0)−bmi]pi}rf(15)
由波波夫积分不等式,及引理1和引理2,可得自适应规律
φ 1 i = − k a i ( t − τ ) v ( τ ) p i y s f ( τ ) , τ ≤ t , i = 0 , 1 , ⋯ , n − 1 φ 2 i = − k a i ′ ( t ) v ( t ) p i y s f ( t ) , i = 0 , 1 , ⋯ , n − 1 ψ 1 i = k b i ( t − τ ) v ( τ ) p i r f ( τ ) , τ ≤ t , i = 0 , 1 , ⋯ , m ψ 2 i = k b i ′ ( t ) v ( t ) p i r f ( t ) , i = 0 , 1 , ⋯ , m (16) \begin{aligned} \varphi_{1 i}&=-k_{a i}(t-\tau) v(\tau) p^{i} y_{s f}(\tau), \quad \tau \leq t, i=0,1, \cdots, n-1 \\ \varphi_{2 i}&=-k_{a i}^{\prime}(t) v(t) p^{i} y_{s f}(t), \quad i=0,1, \cdots, n-1 \\ \psi_{1 i}&=k_{b i}(t-\tau) v(\tau) p^{i} r_{f}(\tau), \quad \tau \leq t, i=0,1, \cdots, m \\ \psi_{2 i}&=k_{b i}^{\prime}(t) v(t) p^{i} r_{f}(t), \quad i=0,1, \cdots, m \end{aligned} \tag{16} φ1iφ2iψ1iψ2i=−kai(t−τ)v(τ)piysf(τ),τ≤t,i=0,1,⋯,n−1=−kai′(t)v(t)piysf(t),i=0,1,⋯,n−1=kbi(t−τ)v(τ)pirf(τ),τ≤t,i=0,1,⋯,m=kbi′(t)v(t)pirf(t),i=0,1,⋯,m(16)
式中, k a i ( t − τ ) k_{a i}(t-\tau) kai(t−τ) 和 k b i ( t − τ ) k_{b i}(t-\tau) kbi(t−τ) 是正定标量积分核,它们的拉普拉斯变化式为在 s = 0 s=0 s=0 处有一极点的正实传递函数; k a i ′ k_{a i}^{\prime} kai′ 和 k b i ′ k_{b i}^{\prime} kbi′ 在 t ≥ 0 t\ge0 t≥0 时为非负标量增益。
三、问题求解
将原题中给定的参考模型和可调系统的传递函数写成输入输出方程的形式:
( 0.0 8 2 p 2 + 2 × 0.08 × 0.75 p + 1 ) y m = r ( T 1 2 p 2 + 2 T 1 ξ 1 p + 1 ) y s f = k 1 r f (17) \begin{gathered} &\left(0.08^{2} p^{2}+2 \times 0.08 \times 0.75 p+1\right) y_{m}=r \\ &\left(T_{1}^{2} p^{2}+2 T_{1} \xi_{1} p+1\right) y_{s f}=k_{1} r_{f} \end{gathered} \tag{17} (0.082p2+2×0.08×0.75p+1)ym=r(T12p2+2T1ξ1p+1)ysf=k1rf(17)
再将上式写成首一古尔维兹多项式的形式:
( p 2 + 2 × 0.08 × 0.75 0.0 8 2 p + 1 0.0 8 2 ) y m = 1 0.0 8 2 r ( p 2 + 2 T 1 ξ 1 T 1 2 + 1 T 1 2 ) y s f = k 1 T 1 2 r f (18) \begin{gathered} \left(p^{2}+\frac{2 \times 0.08 \times 0.75}{0.08^{2}} p+\frac{1}{0.08^{2}}\right) y_{m}=\frac{1}{0.08^{2}} r \\ \left(p^{2}+\frac{2 T_{1} \xi_{1}}{T_{1}^{2}}+\frac{1}{T_{1}^{2}}\right) y_{s f}=\frac{k_{1}}{T_{1}^{2}} r_{f} \end{gathered} \tag{18} (p2+0.0822×0.08×0.75p+0.0821)ym=0.0821r(p2+T122T1ξ1+T121)ysf=T12k1rf(18)
对照(7)式和(11)式,可知相关参数如下:
a m 1 = 2 × 0.08 × 0.75 0.0 8 2 = 18.75 a m 0 = 1 0.0 8 2 = 156.25 b m 0 = 1 0.0 8 2 = 156.25 a s 1 ( v , t ) = 2 T 1 ( t ) ξ 1 ( t ) T 1 2 ( t ) = 2 ( 0.8 − 0.01 t ) ( 0.036 + 0.004 t ) a s 0 ( v , t ) = 1 T 1 2 ( t ) = 1 ( 0.036 + 0.004 t ) 2 b s 0 ( v , t ) = k 1 ( t ) T 1 2 ( t ) = 1.12 − 0.008 t ( 0.036 + 0.004 t ) 2 (19) \begin{aligned} &a_{m 1}=\frac{2 \times 0.08 \times 0.75}{0.08^{2}}=18.75 \\ &a_{m 0}=\frac{1}{0.08^{2}}=156.25 \\ &b_{m 0}=\frac{1}{0.08^{2}}=156.25 \\ &a_{s 1}(v, t)=\frac{2 T_{1}(t) \xi_{1}(t)}{T_{1}^{2}(t)}=\frac{2(0.8-0.01 t)}{(0.036+0.004 t)} \\ &a_{s 0}(v, t)=\frac{1}{T_{1}^{2}(t)}=\frac{1}{(0.036+0.004 t)^{2}} \\ &b_{s 0}(v, t)=\frac{k_{1}(t)}{T_{1}^{2}(t)}=\frac{1.12-0.008 t}{(0.036+0.004 t)^{2}} \end{aligned} \tag{19} am1=0.0822×0.08×0.75=18.75am0=0.0821=156.25bm0=0.0821=156.25as1(v,t)=T12(t)2T1(t)ξ1(t)=(0.036+0.004t)2(0.8−0.01t)as0(v,t)=T12(t)1=(0.036+0.004t)21bs0(v,t)=T12(t)k1(t)=(0.036+0.004t)21.12−0.008t(19)
进而可知, a s 1 ( 0 ) ≈ 44.4 a_{s 1}(0) \approx 44.4 as1(0)≈44.4, a s 0 ( 0 ) ≈ 771.6 a_{s 0}(0) \approx 771.6 as0(0)≈771.6, b s 0 ( 0 ) ≈ 864.2 b_{s 0}(0) \approx 864.2 bs0(0)≈864.2。
设输出的广义误差为
ε f = y m f − y s f (20) \varepsilon_{f}=y_{m f}-y_{s f} \tag{20} εf=ymf−ysf(20)
串联补偿器方程为
v = D ( p ) ε f = ( d 1 p + d 0 ) ε f (21) v=D(p) \varepsilon_{f}=\left(d_{1} p+d_{0}\right) \varepsilon_{f} \tag{21} v=D(p)εf=(d1p+d0)εf(21)
选取的自适应规律如下
a s i ( v , t ) = ∫ 0 t φ 1 i ( v , t , τ ) d τ + φ 2 i ( v , t ) + a s i ( 0 ) , i = 0 , 1 b s 0 ( v , t ) = ∫ 0 t ψ 10 ( v , t , τ ) d τ + ψ 20 ( v , t ) + b s 0 ( 0 ) (22) \begin{aligned} a_{s i}(v, t)&=\int_{0}^{t} \varphi_{1 i}(v, t, \tau) d \tau+\varphi_{2 i}(v, t)+a_{s i}(0), i=0,1 \\ b_{s 0}(v, t)&=\int_{0}^{t} \psi_{10}(v, t, \tau) d \tau+\psi_{20}(v, t)+b_{s 0}(0) \end{aligned} \tag{22} asi(v,t)bs0(v,t)=∫0tφ1i(v,t,τ)dτ+φ2i(v,t)+asi(0),i=0,1=∫0tψ10(v,t,τ)dτ+ψ20(v,t)+bs0(0)(22)
参考(16)式的形式,可得可调参数的自适应规律如下:
φ 10 = − k a 0 ( t − τ ) v ( τ ) y s f ( τ ) , τ ≤ t φ 20 = − k a 0 ′ ( t ) v ( t ) y s f ( t ) φ 11 = − k a 1 ( t − τ ) v ( τ ) p y s f ( τ ) , τ ≤ t φ 21 = − k a 1 ′ ( t ) v ( t ) p y s f ( t ) ψ 10 = k b 0 ( t − τ ) v ( τ ) r f ( τ ) , τ ⩽ t ψ 20 = k b 0 ′ ( t ) v ( t ) r f ( t ) (23) \begin{aligned} \varphi_{1 0}&=-k_{a 0}(t-\tau) v(\tau) y_{sf}(\tau), \quad \tau \le t \\ \varphi_{2 0}&=-k_{a 0}^{\prime}(t) v(t) y_{s f}(t) \\ \varphi_{1 1}&=-k_{a 1}(t-\tau) v(\tau) p y_{sf}(\tau), \quad \tau \le t \\ \varphi_{2 1}&=-k_{a 1}^{\prime}(t) v(t) p y_{s f}(t) \\ \psi_{1 0}&=k_{b 0}(t-\tau) v(\tau) r_{f}(\tau), \quad \tau \leqslant t \\ \psi_{2 0}&=k_{b 0}^{\prime}(t) v(t) r_{f}(t) \end{aligned} \tag{23} φ10φ20φ11φ21ψ10ψ20=−ka0(t−τ)v(τ)ysf(τ),τ≤t=−ka0′(t)v(t)ysf(t)=−ka1(t−τ)v(τ)pysf(τ),τ≤t=−ka1′(t)v(t)pysf(t)=kb0(t−τ)v(τ)rf(τ),τ⩽t=kb0′(t)v(t)rf(t)(23)
式中, k a 0 ( t − τ ) k_{a 0}(t-\tau) ka0(t−τ)、 k a 1 ( t − τ ) k_{a 1}(t-\tau) ka1(t−τ) 和 k b 0 ( t − τ ) k_{b 0}(t-\tau) kb0(t−τ) 为正定积分核, k a 0 ′ ( t ) k_{a 0}^{\prime}(t) ka0′(t)、 k a 1 ′ ( t ) k_{a 1}^{\prime}(t) ka1′(t) 和 k b 0 ′ ( t ) k_{b 0}^{\prime}(t) kb0′(t) 对 ∀ t ≥ 0 \forall t \ge 0 ∀t≥0 均为非负标量增益。
下面再讨论一下引入的串联补偿器中的参数 d 0 d_0 d0 和 d 1 d_1 d1 的取值范围,系统的等价前向线性方块传递函数为:
h ( s ) = d 1 ( s ) + d 0 s 2 + a m 1 s + a m 0 (24) h(s)=\frac {d_1(s)+d_0} {s^2+a_{m1}s+a_{m0}} \tag{24} h(s)=s2+am1s+am0d1(s)+d0(24)
其对应的能控标准型如下:
e ˙ = A m e + b ω 1 v = d T e (25) \begin{aligned} \boldsymbol{\dot e} &= \boldsymbol{A_m} \boldsymbol{e} + b \omega_1 \\ v &= d^T \boldsymbol{e} \end{aligned} \tag{25} e˙v=Ame+bω1=dTe(25)
式中, e = [ ε ε ˙ ] \boldsymbol{e}=\left[ \begin{matrix} \varepsilon \\ \dot \varepsilon \end{matrix} \right] e=[εε˙], A m = [ 0 1 − a m 0 − a m 1 ] \boldsymbol{A_m}=\left[ \begin{matrix} 0 & 1 \\ -a_{m0} & -a_{m1} \end{matrix} \right] Am=[0−am01−am1], b = [ 0 1 ] b=\left[ \begin{matrix} 0 \\ 1 \end{matrix} \right] b=[01], d = [ d 0 d 1 ] d=\left[ \begin{matrix} d_0 \\ d_1 \end{matrix} \right] d=[d0d1]。
要求 h ( s ) h(s) h(s) 是一个严格正实传递函数,则必定存在正定对称矩阵 P P P 和 Q Q Q,使方程式(26)成立:
{ P A m + A m T P = − Q P b = d (26) \left\{ \begin{aligned} &P A_m + A_m^T P = -Q\\ &P b = d \end{aligned} \right. \tag{26} { PAm+AmTP=−QPb=d(26)
由此可解得:
d 0 > 0 , d 1 d 0 > 1 a m 1 = 0.053 (27) d_0 > 0, \quad \frac {d_1} {d_0} > \frac {1} {a_{m_1}} =0.053 \tag{27} d0>0,d0d1>am11=0.053(27)
最终搭建的仿真模型框图如 图1 所示:

具体的 Simulink 仿真文件我已上传至百度网盘中,链接如下:experiment_3.slx_免费高速下载|百度网盘-分享无限制 (baidu.com)
输入信号与广义输出误差信号如 图2 所示:

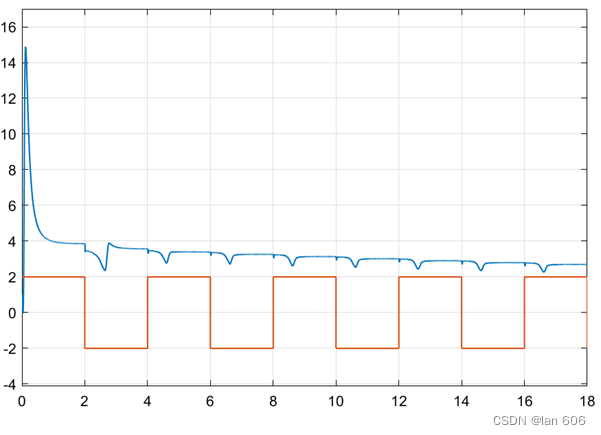
输入信号与增益信号如 图3 所示:
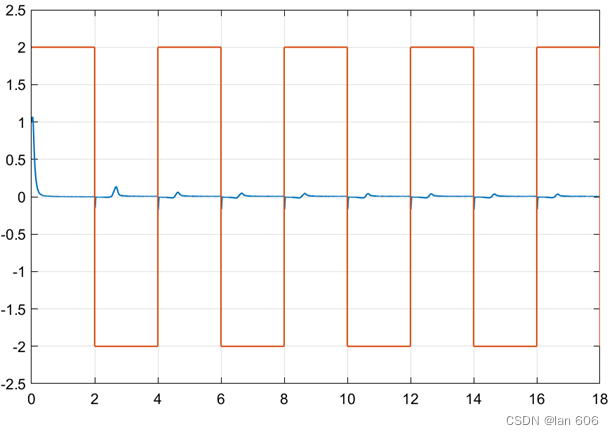
输入信号与可调参数1的变化曲线如 图4 所示:

输入信号与可调参数2的变化曲线如 图5 所示:
参考书目
李言俊, 张科. 自适应控制理论及应用[M]. 西北工业大学出版社, 2005.
边栏推荐
猜你喜欢

UnityShader入门学习(三)——Unity的Shader

纸质说明书秒变3D动画,斯坦福大学吴佳俊最新研究,入选ECCV 2022
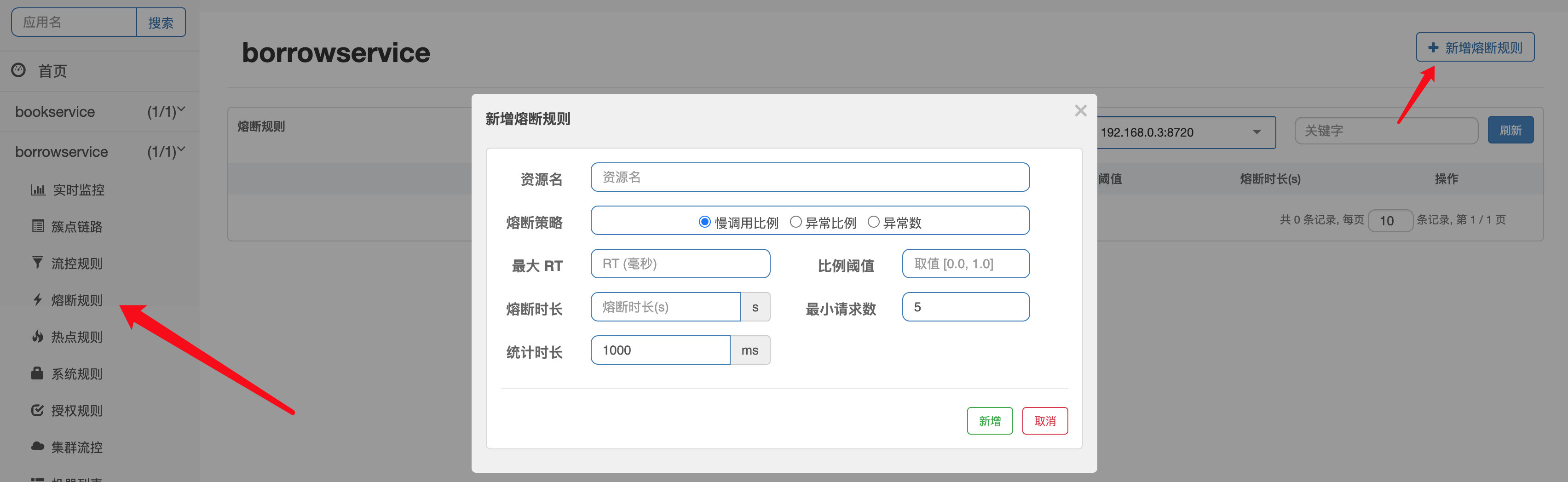
Sentinel服务熔断和降级

MySQL has played to such a degree, no wonder the big manufacturers are rushing to ask for it!

The recently popular domestic interface artifact Apipost experience

2021 OWASP TOP 10 漏洞指南

I summed up the bad MySQL interview questions
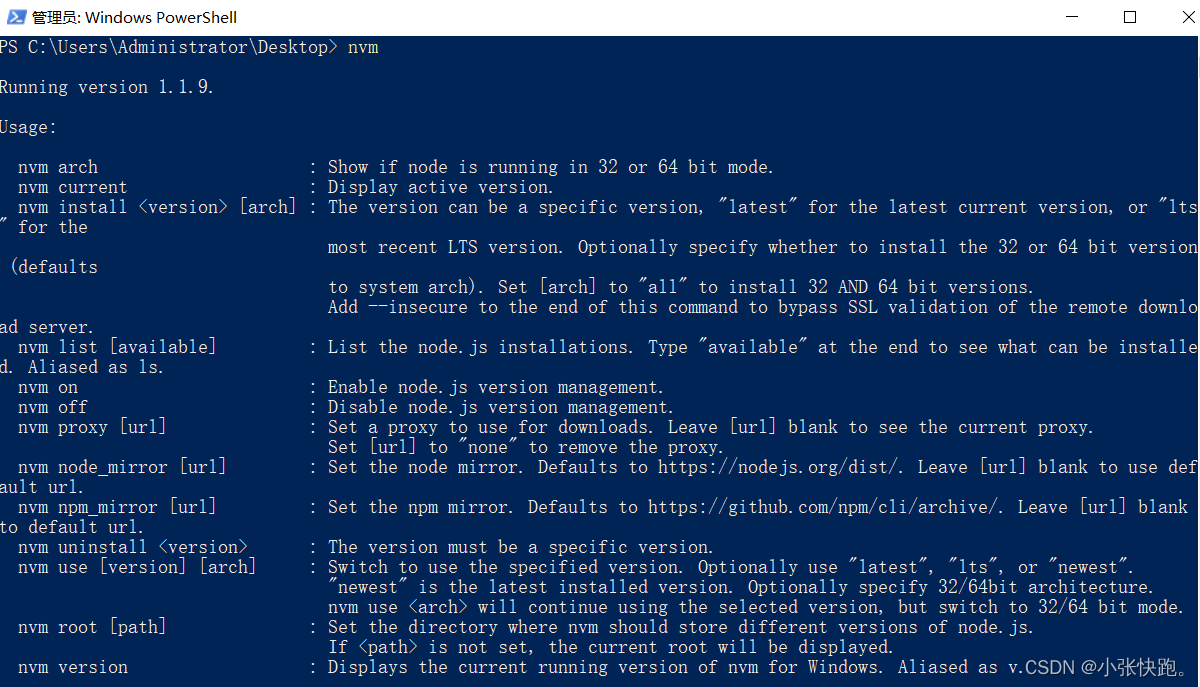
Node version switching management using NVM

IDEA connects to MySQL database and uses data

2021 OWASP TOP 10 Vulnerability Guide
随机推荐
ADS communicate with c #
Sentinel流量控制
R语言的画图代码及差异性分析[通俗易懂]
C language basic practice (nine-nine multiplication table) and printing different asterisk patterns
leetcode: 485. Maximum number of consecutive 1s
2021 OWASP TOP 10 漏洞指南
常用工具命令速查表
I summed up the bad MySQL interview questions
五个维度着手MySQL的优化
The magic of SQL MERGE statement (detailed instructions)
AWS实现定时任务-Lambda+EventBridge
Numbers that appear only once in LeetCode
MySQL [aggregate function]
LeetCode旋转数组
OAuth2:搭建授权服务器
OpenShift 4 - 定制 RHACS 安全策略,阻断生产集群使用高风险 Registry
Unity study notes Description of AVPro video jump function (Seeking)
Combination series - there are combinations when there are arrangements
The recently popular domestic interface artifact Apipost experience
架构实战营模块8消息队列表结构设计