当前位置:网站首页>Learning records on July 4, 2022
Learning records on July 4, 2022
2022-07-07 06:51:00 【a simple_ boy】
Simple XOR problem ( structure + Exclusive or )
Description:
There is a set of integers {0,1,2,…,2^m−1}, Please choose from them k Number , Make this k The XOR sum of numbers is n, Please output the maximum qualified k.
Solution:
Since you want to choose the most k So we can think of 0 and x XOR is x Let's make as many numbers as possible exclusive or and as 0 Last one x
Yes On ren What [ 0 , 2 m − 1 ] in , for example 0 ⊕ 7 = 1 ⊕ 6 = 2 ⊕ 5 = 3 ⊕ 4 = 0 that Well total different or and Just by 0 the With Such as fruit I People Need to be want One individual Count n Of word , I People Just Meeting take belt Yes n Of Count Yes Demolition fall , And Go to fall n Of another One individual , this yes One like love condition , Especially love condition Just yes When n and m , other Small Of when Hou I People Need to be want branch class please On One Next edge world love condition When n = = 0 And m ! = 1 Of when Hou , I People can With One individual all No Go to fall , k = 2 m When n = = 1 And m = = 1 Of when Hou , k = 2 Its more than love condition , all by just often love condition , Yes k = 2 m − 1 For any [0, 2^m-1] in , give an example 0\oplus7 = 1\oplus6 = 2\oplus5 = 3\oplus4 = 0 \\ Then total XOR and is 0\\ So if we need a number n Words , We will bring n Remove the number of pairs , And get rid of it n Another , This is the general situation \\ The special case is when n and m When I was very young We need to discuss the boundary conditions by categories \\ When n==0 And m!=1 When , We can remove none ,k=2^m\\ When n==1 And m==1 When ,k=2\\ Other cases , All are normal , Yes k=2^m-1 Yes On ren What [0,2m−1] in , for example 0⊕7=1⊕6=2⊕5=3⊕4=0 that Well total different or and Just by 0 the With Such as fruit I People Need to be want One individual Count n Of word , I People Just Meeting take belt Yes n Of Count Yes Demolition fall , And Go to fall n Of another One individual , this yes One like love condition , Especially love condition Just yes When n and m , other Small Of when Hou I People Need to be want branch class please On One Next edge world love condition When n==0 And m!=1 Of when Hou , I People can With One individual all No Go to fall ,k=2m When n==1 And m==1 Of when Hou ,k=2 Its more than love condition , all by just often love condition , Yes k=2m−1
Code:
int main()
{
cin >> n >> m;
LL res = (1LL << m);
if(n == 0 && m != 1)
cout << res << '\n';
else if(n == 1 && m == 1)
cout << 2 << '\n';
else
cout << res - 1LL << '\n';
}
Perfect number ( structure + Permutation and combination )
Description:
For a given number a , b , When the whole number n All digits in the decimal system are a or b when , We call n yes “ Good number ”
For good numbers n , When n In the decimal system, the sum of each digit is also “ Good number ” when , We call n It's a “ Perfect number ”
Please find out how many m The number of digits is “ Perfect number ”
(1≤m≤1e6,1≤a,b≤9).
Solution:
because m It's big What you think dfs Violence doesn't work O(2^m) I don't think it will be so simple
Why? dfs So slow Because for everyone, I have confirmed that he is a still b If I avoid this, I can save a lot of time
So we think of enumeration a and b Respective quantity But do not consider its placement Spend time O(n)
While enumerating Verify whether the scheme is feasible It's about constant time
When the plan is feasible We need to update the answer How to update Suppose there is x individual a n-x individual b This is a legal scheme
Because the scheme has nothing to do with the placement order So this x individual a It can be placed on any number of digits At this time, an arrangement and combination method comes to mind
Code:
const int N = 1e6 + 5, mod = 1e9 + 7;
int a, b;
LL m;
LL fac[N], inv[N];
LL qmi(int a, int b)
{
LL res = 1;
while(b)
{
if(b & 1) res = res * a % mod;
a = a * 1LL * a % mod;
b >>= 1;
}
return res;
}
void init()
{
inv[0] = fac[0] = 1;
rep(i, 1, N)
fac[i] = i * fac[i - 1] % mod;
inv[N - 1] = qmi(fac[N - 1], mod - 2);
for(int i = N - 2; i; i --)
inv[i] = inv[i + 1] * (i + 1) % mod;
}
LL C(int a, int b)
{
return (fac[a] * inv[b] % mod * inv[a - b] % mod) % mod;
}
// Combinatorial math board
int main()
{
cin >> a >> b >> m;
init();
LL res = 0;
rep(i, 0, m + 1) // choose i individual b m-i individual a Combine
{
LL last = m - i;
LL num = last * a + i * b;
bool flag = 1;
while(num)
{
if(num % 10 != a && num % 10 != b)
{
flag = false;
break;
}
num /= 10;
}
if(flag)
res = (res + C(m, i)) % mod;
}
cout << res;
}
Number combination (01 Knapsack for the number of solutions )
Description:
Given N A positive integer A_1,A_2,…,A_N, Choose a number from them , Make their sum for M, Find out how many options there are .
N < 100, M < 10000, A_i < 1000
Solution:
We can define an array dp[ j ], Express and for j How many schemes are there
obviously dp[0] = 1
The transfer equation is dp[j] += dp[j - a[i]]
Code:
int main()
{
cin >> n >> m;
rep(i, 1, n + 1)
cin >> a[i];
dp[0] = 1;
rep(i, 1, n + 1)
for(int j = m; j >= a[i]; j --)
dp[j] += dp[j - a[i]];
cout << dp[m];
}
Natural number splitting ( Complete knapsack solution number )
Description:
Given a natural number N, Ask for N Split into the form of adding several positive integers , The number participating in the addition operation can be repeated .
- The splitting scheme does not consider the order ;
- At least split into 2 The number and .
Solution:
This problem is still the number of schemes for summation , But the difference between the previous question is that each number can only be selected once However, you can choose any number in this question , So this is 01 The difference between a backpack and a complete backpack
Define an array dp[ j ] Express and for j Number of alternatives
dp[0] = 1
The transfer equation is dp[j] += dp[j - a[i]]
Code:
int main()
{
cin >> n;
dp[0] = 1;
for(int i = 1; i < n; i ++) //[1, n - 1]
for(int j = i; j <= n; j ++)
dp[j] = (dp[j] + dp[j - i]) % mod;
cout << dp[n];
}
Record the interval DP Board question : Merge stones
Merge two adjacent piles of stones at a time , The combination cost is the quality of two piles of stones and , Due to the different order of consolidation , Therefore, the price paid is different , The merge length is n What is the minimum cost of the stone
N = 300
Let's take a look at the interval DP The concept of
Section DP Is to solve linear DP When dividing the problem in stages , Arising from problems related to sequence and merger
Its main features are divided into the following three points
- Merge : Integrate two or more parts , Or split
- features : Decompose the problem into two combined forms
- solve : Set the optimal value for the whole problem , Enumerate merge points , Divide the problem into two parts , Finally, the optimal value of the whole problem is obtained by merging the optimal values of the two parts
For this question We need to set dp[ i ] [ j ] To express and merge [i, j] The minimum cost of
Through the interval DP Characteristics It is not difficult for us to write the transfer equation dp[ i ] [ j ] = min(dp[i] [k] + dp[k + 1] [j] + The cost of merging )
Because the interval dp The nature of It is to divide a problem into left and right parts So we must know the small part first Can we recursively solve to a large part This determines the interval DP Traversal order in In other words, we must first get the optimal value of the interval with smaller length Then the optimal value is obtained by recursion to the interval with larger length
// The core code of this topic
memset(dp, 0x3f, sizeof dp);
for(int len = 1; len <= n; len ++)
{
for(int i = 1; i + len - 1 <= n; i ++)
{
int j = i + len - 1;
if(len == 1) // Initialize to 0
dp[i][j] = 0;
else // if len Not for 1 Start tweeting
{
for(int k = i; k < j; k ++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1]); //s Represents prefix and array
}
}
}
// Practice mnemonic search
int dfs(int s, int e)
{
if(s == e) return 0;
int &v = dp[s][e];
if(v != -1) return v;
v = 1e9;
for(int k = s; k < e; k ++)
v = min(v, dfs(s, k) + dfs(k + 1, e) + pre_[e] - pre_[s - 1]);
return v;
}
Tomorrow's set CF Brush interval DP subject
边栏推荐
- 联合索引ABC的几种索引利用情况
- Basic introduction of JWT
- 2018年江苏省职业院校技能大赛高职组“信息安全管理与评估”赛项任务书
- LM11丨重构K线构建择时交易策略
- BindingException 异常(报错)处理
- RuntimeError: CUDA error: CUBLAS_STATUS_ALLOC_FAILED when calling `cublasCreate(handle)`问题解决
- Jmeter 5.5版本发布说明
- 从零到一,教你搭建「CLIP 以文搜图」搜索服务(二):5 分钟实现原型
- Tkinter window selects PCD file and displays point cloud (open3d)
- Stack and queue-p79-9
猜你喜欢

Abnova循环肿瘤DNA丨全血分离,基因组DNA萃取分析

How can I check the DOI number of a foreign document?
Installing redis and windows extension method under win system
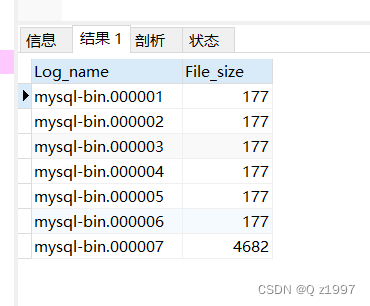
mysql查看bin log 并恢复数据
场馆怎么做体育培训?
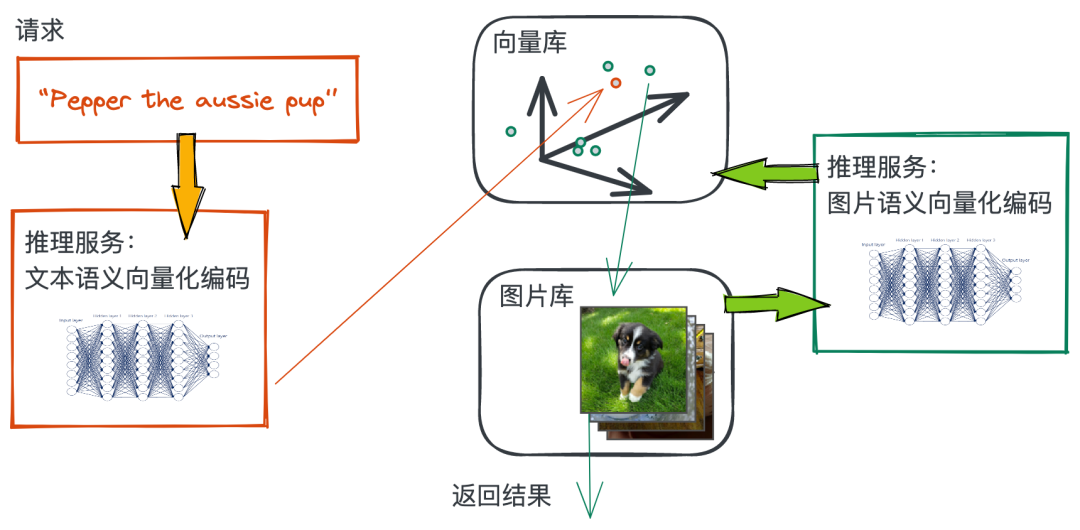
从零到一,教你搭建「CLIP 以文搜图」搜索服务(二):5 分钟实现原型
Matlab tips (30) nonlinear fitting lsqcurefit
![[noi simulation] regional division (conclusion, structure)](/img/7d/4c66cd0a30e52ccd167b6138fcb4df.png)
[noi simulation] regional division (conclusion, structure)
Config分布式配置中心

请问如何查一篇外文文献的DOI号?
随机推荐
Redis (II) - redis General Command
LM11丨重构K线构建择时交易策略
精准时空行程流调系统—基于UWB超高精度定位系统
肿瘤免疫治疗研究丨ProSci LAG3抗体解决方案
unity3d学习笔记
impdp的transform参数的测试
根据IP获取地市
联合索引ABC的几种索引利用情况
sqlserver多线程查询问题
项目实战 五 拟合直线 获得中线
Learning notes | data Xiaobai uses dataease to make a large data screen
Abnova循环肿瘤DNA丨全血分离,基因组DNA萃取分析
Unity C# 函数笔记
libcurl返回curlcode说明
工具类:对象转map 驼峰转下划线 下划线转驼峰
Go straight to the 2022ecdc fluorite cloud Developer Conference: work with thousands of industries to accelerate intelligent upgrading
Several index utilization of joint index ABC
网络基础 —— 报头、封装和解包
MySQL的主从复制原理
MySQL卸载文档-Windows版