当前位置：网站首页>LeetCode刷题day49

LeetCode刷题day49

2022-07-07 15:35:00 【51CTO】

今日刷题重点—贪心

文章目录

55. 跳跃游戏

题目描述
思路分析
参考代码

45. 跳跃游戏 II

题目描述
思路分析
参考代码

1005. K 次取反后最大化的数组和

题目描述
思路分析
参考代码

55. 跳跃游戏

题目描述

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

示例 2：

       
       输入：nums 
       
       = [
       
       3,
       
       2,
       
       1,
       
       0,
       
       4]
       
       输出：false
       
       解释：无论怎样，总会到达下标为 
       
       3 
       
       的位置。但该下标的最大跳跃长度是 
       
       0
      
1.
2.
3.

思路分析

刚看到本题一开始可能想：当前位置元素如果是3，我究竟是跳一步呢，还是两步呢，还是三步呢，究竟跳几步才是最优呢？

其实跳几步无所谓，关键在于可跳的覆盖范围！

这个范围内，别管是怎么跳的，反正一定可以跳过来。

那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

局部最优推出全局最优，找不出反例，试试贪心！

如图：

LeetCode刷题day49_i++

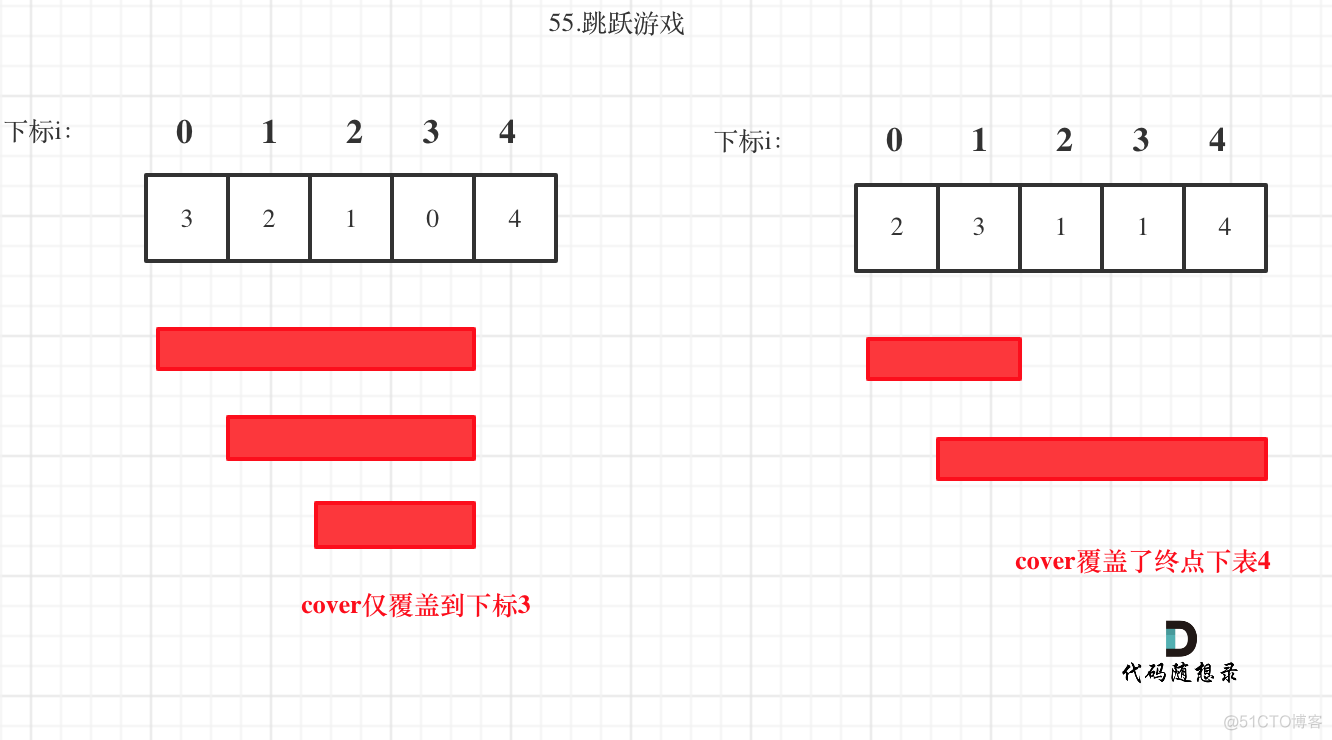
i每次移动只能在cover的范围内移动，每移动一个元素，cover得到该元素新的覆盖范围的补充，让i继续移动下去。

而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。

如果cover大于等于了终点下标，直接return true就可以了。

参考代码

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       bool 
       
       canJump(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums) { 
       
       int 
       
       cover 
       
       = 
       
       0;
       
       //最远到达(覆盖)的位置
       
       if(
       
       nums.
       
       size()
       
       ==
       
       1) { 
       
       //只有一个元素则直接结束.
       
       return 
       
       true;
       
  }
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       <= 
       
       cover; 
       
       i
       
       ++) {
       
       //范围是0-cover,每次跳跃是在cover范围内的 
       
       cover 
       
       = 
       
       max(
       
       nums[
       
       i]
       
       +
       
       i,
       
       cover);
       
       //求个最大值
       
       if(
       
       cover
       
       >=
       
       nums.
       
       size()
       
       -
       
       1) {
       
       //结束
       
       return 
       
       true;
       
    }
       
  }
       
       return 
       
       false;
       
       //如果元素遍历完毕cover还没到达最后一个元素下标,则不可能到达.
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

45. 跳跃游戏 II

题目描述

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例 1:

       
       输入: 
       
       nums 
       
       = [
       
       2,
       
       3,
       
       1,
       
       1,
       
       4]
       
       输出: 
       
       2
       
       解释: 
       
       跳到最后一个位置的最小跳跃数是 
       
       2
       
       。
       
       从下标为 
       
       0 
       
       跳到下标为 
       
       1 
       
       的位置，跳 
       
       1 
       
       步，然后跳 
       
       3
      
1.
2.
3.
4.

示例 2:

思路分析

本题要计算最小步数，那么就要想清楚什么时候步数才一定要加一呢？

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。

思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围.覆盖范围一旦覆盖了终点，得到的就是最小步数！

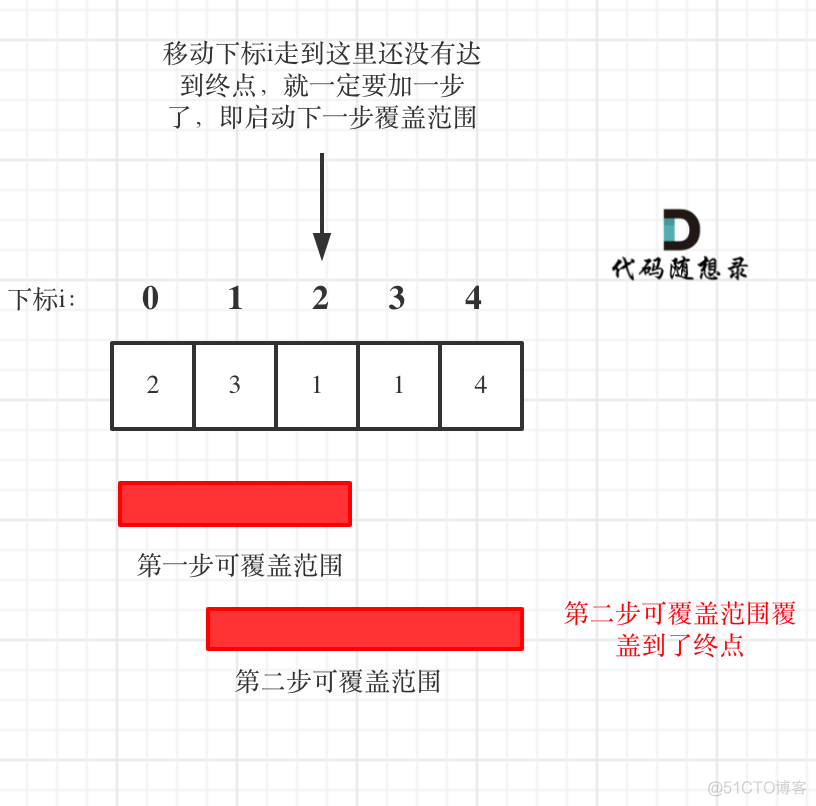
这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如图：

LeetCode刷题day49_i++_02

参考代码

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       int 
       
       jump(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums) {
       
       if(
       
       nums.
       
       size()
       
       ==
       
       1){
       
       return 
       
       0;
       
  }
       
       int 
       
       curDistance 
       
       = 
       
       0;
       
       //当前最远 覆盖的下标
       
       int 
       
       nextDistance 
       
       = 
       
       0;
       
       //下一步最远覆盖的下标
       
       int 
       
       ans 
       
       = 
       
       0;
       
       //走的步数
       
       for(
       
       int 
       
       i 
       
       = 
       
       0;
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       nextDistance 
       
       = 
       
       max(
       
       nums[
       
       i]
       
       +
       
       i,
       
       nextDistance);
       
       //更新nextDistance (在走当前这一步的时候) 
       
       if(
       
       i
       
       ==
       
       curDistance){
       
       //相等时,说明可能需要再往前走一步了. 
       
       if(
       
       i
       
       !=
       
       nums.
       
       size()
       
       -
       
       1){
       
       //还没到达,则一定需要继续走 
       
       ans
       
       ++; 
       
       curDistance 
       
       = 
       
       nextDistance;
       
       //更新覆盖范围
       
       if(
       
       curDistance 
       
       >= 
       
       nums.
       
       size()
       
       -
       
       1) {
       
       //如果新走的这一步可以到达终点,则直接结束循环 
       
       break;
       
       //这三行if代码,算是优化吧,不写只是在走到这个点会进行判断.
       
        }
       
      }
       
       else{
       
       //如果相等,则不用往前走了. 
       
       break;
       
      } 
       
    }
       
  } 
       
       return 
       
       ans; 
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.

1005. K 次取反后最大化的数组和

题目描述

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标i 并将nums[i] 替换为-nums[i] 。

重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例 1：

示例 2：

示例 3：

思路分析

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让数组和达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比反转5得到的-5 大多了），全局最优：整个数组和达到最大。

那么本题的解题步骤为：

第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
第二步：从前向后遍历，遇到负数将其变为正数，同时K–
第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
第四步：求和

参考代码

       
       #include<bits/stdc++.h>
       
       using 
       
       namespace 
       
       std;
       
       static 
       
       bool 
       
       cmp(
       
       int 
       
       a,
       
       int 
       
       b){
       
       //按照绝对值大的排在前面 
       
       return 
       
       abs(
       
       a) 
       
       > 
       
       abs(
       
       b);
       
}
       
       int 
       
       largestSumAfterKNegations(
       
       vector
       
       <
       
       int
       
       >& 
       
       nums, 
       
       int 
       
       k) {
       
       int 
       
       ans 
       
       = 
       
       0;
       
       sort(
       
       nums.
       
       begin(),
       
       nums.
       
       end());
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       if(
       
       nums[
       
       i] 
       
       < 
       
       0 
       
       && 
       
       k 
       
       > 
       
       0) {
       
       nums[
       
       i]
       
       *=-
       
       1;
       
       k
       
       --;
       
    }
       
  }
       
       if(
       
       k 
       
       % 
       
       2 
       
       == 
       
       1){ 
       
       //如果k还有剩余,就选最小的数 反复*-1,直至k用完即可
       
       nums[
       
       nums.
       
       size()
       
       -
       
       1] 
       
       *= 
       
       -
       
       1;
       
  }
       
       for(
       
       int 
       
       i 
       
       = 
       
       0; 
       
       i 
       
       < 
       
       nums.
       
       size(); 
       
       i
       
       ++){
       
       ans 
       
       += 
       
       nums[
       
       i];
       
  }
       
       return 
       
       ans;
       
}
      
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.