Path problem before Dynamic Planning

routing problem ： This chapter only talks about different paths （Leecode 62）、 Different paths （Leecode 63）、 Paths and issues （Leedcode 64）

---

Tips ： After writing the article , Directories can be generated automatically , How to generate it, please refer to the help document on the right

---

Preface

Path problem is the prequel of knapsack problem as a classical dynamic programming problem , For understanding dp The thought model of dynamic programming .

One 、 Different path problems （Leecode 62 secondary ）

1. Problem description

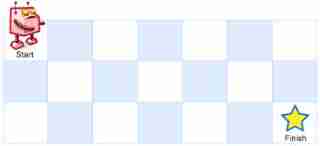
A robot is in a m x n The top left corner of the grid （ The starting point is marked as “Start” ）. The robot can only move down or right one step at a time . The robot tries to reach the bottom right of the grid （ In the figure below, it is marked as “Finish” ）. Ask how many different paths there are in total ？

2. Problem analysis

 In fact, dynamic problems only need to consider how to define the data structure 、 The meaning of structure 、 Establishment of state transition equation .

2.1 Define the data structure

The question is how many different paths , In this case, you should use dp[m-1][n-1] To express the final result , The example in the last blog is the longest palindrome string , Namely dp[i][j] To express from i To j String ,leedcode 678 The longest increasing subsequence of can be used dp[i] To express , Because it's continuous .

2.2 Interpretation of structural meaning

In this question dp[i][j] It can be interpreted as ：i Represents the row of the map ,j Representative column
In the longest palindrome string dp[i][j]：i Is the starting point of palindrome string idx,j Is the end of the palindrome string
The longest increasing subsequence ：dp[i] Is the end of the subsequence idx, Because the starting point is the end of the last cycle , So you don't need to define it as a two-dimensional array , Defined as a two-dimensional array to traverse will exceed the time limit , It takes too long

2.3 Establishment of state transition equation

In this question ：
Due to the limitation of the topic, we can only go down or to the right Move , So we follow 「 Current optional direction 」 Analyze ：
Current location can only 「 Down 」 Move , That is to say dp[i][j] = dp[i-1][j]
Current location can only 「 To the right 」 Move , That is to say dp[i][j] = dp[i][j-1]
The current position can 「 Down 」 Can also 「 To the right 」 Move , That is to say dp[i][j] =dp[i][j-1] + dp[i-1][j]
Derivation process ：
dp[i][j] It represents the arrival map grid[i][j] The number of points reaching the path , Then step up ： How to get there grid[i][j] spot , There are only two ways ： Enter this point from the front point down or to the right , So arrive at grid[i][j] The only way is to arrive dp[i][j-1] The way + arrive dp[i-1][j] The way , From this we can deduce dp[i][j] State transfer equation of ：dp[i][j] =dp[i][j-1] + dp[i-1][j]

3. Code display ：

The code is as follows （ Example ）：

class Solution {
    
public:
    int uniquePaths(int m, int n) {
    
        vector<vector<int>> dp(m, vector<int>(n));
        dp[0][0]=1;
        for(int i=0;i<m;i++)
        {
    
            for(int j=0;j<n;j++)
            {
    
                if(i>0&&j>0)
                {
    
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
                else if(i>0)
                {
    
                    dp[i][j]=dp[i-1][j];
                }
                else if(j>0){
    
                     dp[i][j]=dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

Two 、 Different path problems ll（Leecode 63 secondary ）

1. Problem description

This is a LeetCode Upper 「63. Different paths II」, The difficulty is Medium.
A robot is in a m x n The top left corner of the grid （ The starting point is marked as “Start” ）. The robot can only move down or right one step at a time . The robot tries to reach the bottom right corner of the grid ( In the figure below, it is marked as “Finish”）. Now consider the obstacles in the grid . So how many different paths will there be from the top left corner to the bottom right corner ？ Obstacles and empty positions in the grid are used respectively 1 and 0 To express .

2. Problem analysis

 In fact, dynamic problems only need to consider how to define the data structure 、 The meaning of structure 、 Establishment of state transition equation .

2.1 Define the data structure

The question is how many different paths , In this case, you should use dp[m-1][n-1] To express the final result

2.2 Interpretation of structural meaning

In this question dp[i][j] It can be interpreted as ：i Represents the row of the map ,j Representative column

2.3 Establishment of state transition equation

In this question ：
Due to the limitation of the topic, we can only go down or to the right Move , So we follow 「 Current optional direction 」 Analyze ：
Current location can only 「 Down 」 Move , That is to say dp[i][j] = dp[i-1][j]
Current location can only 「 To the right 」 Move , That is to say dp[i][j] = dp[i][j-1]
The current position can 「 Down 」 Can also 「 To the right 」 Move , That is to say dp[i][j] =dp[i][j-1] + dp[i-1][j]
Derivation process ：
dp[i][j] It represents the arrival map grid[i][j] The number of points reaching the path , Then step up ： How to get there grid[i][j] spot , There are only two ways ： Enter this point from the front point down or to the right , So arrive at grid[i][j] The only way is to arrive dp[i][j-1] The way + arrive dp[i-1][j] The way , Of course, the difference between this problem and another problem is ： Whether the last point can be moved left or right , From this we can deduce dp[i][j] State transfer equation of ：dp[i][j] =dp[i][j-1] + dp[i-1][j], The equation of state does not change , But the conditions must be controlled ：i>0&&j>0&&obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==0

3. Code display ：

The code is as follows （ Example ）：

class Solution {
    
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
    
        int n=obstacleGrid[0].size();
        int m=obstacleGrid.size();
         vector<vector<int>> dp(m, vector<int>(n));
        dp[0][0]=1;
        if(obstacleGrid[m-1][n-1]==1)
        {
    
            return 0;
        }
        for(int i=0;i<m;i++)
        {
    
            for(int j=0;j<n;j++)
            {
    
                if(i>0&&j>0&&obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==0)
                {
    
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
                else if(i>0&&obstacleGrid[i-1][j]==0)
                {
    
                    dp[i][j]=dp[i-1][j];
                }
                else if(j>0&&obstacleGrid[i][j-1]==0){
    
                     dp[i][j]=dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

---

Two 、 Minimum path sum （Leecode 64 secondary ）

1. Problem description

Given a... That contains a nonnegative integer m x n grid grid , Please find a path from the top left corner to the bottom right corner , Make the sum of the numbers on the path the smallest .
explain ： You can only move down or right one step at a time

2. Problem analysis

 In fact, dynamic problems only need to consider how to define the data structure 、 The meaning of structure 、 Establishment of state transition equation .

2.1 Define the data structure

The question is how many different paths , In this case, you should use dp[m-1][n-1] To express the final result

2.2 Interpretation of structural meaning

In this question dp[i][j] It can be interpreted as ：i Represents the row of the map ,j Representative column

2.3 Establishment of state transition equation

In this question ：
Due to the limitation of the topic, we can only go down or to the right Move , So we follow 「 Current optional direction 」 Analyze ：
Current location can only 「 Down 」 Move , That is to say dp[i][j] = dp[i-1][j]
Current location can only 「 To the right 」 Move , That is to say dp[i][j] = dp[i][j-1]
The current position can 「 Down 」 Can also 「 To the right 」 Move , That is to say dp[i][j] =dp[i][j-1] + dp[i-1][j]
Derivation process ：
dp[i][j] It represents the arrival map grid[i][j] The sum of the numbers of points reaching the path , Then step up ： How to get there grid[i][j] spot , There are only two ways ： Enter this point from the front point down or to the right , You'll get （dp[i][j-1] The sum of the numbers +grid[i][j]）、（dp[i-1][j] The sum of the numbers of +grid[i][j]） Two ways , The result of the problem is to find the one with the smallest number , So just find the smallest one in these two ways , because dp[i][j-1]、dp[i-1][j] These two methods are the minimum value before , So the calculation is dp[i][j] Is the smallest . From this we can deduce dp[i][j] State transfer equation of ：dp[i][j]=min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])

3. Code display ：

The code is as follows （ Example ）：

class Solution {
    
public:
    int minPathSum(vector<vector<int>>& grid) {
    
        int n=grid[0].size();
        int m=grid.size();
         vector<vector<int>> dp(m, vector<int>(n));
        dp[0][0]=grid[0][0];
        for(int i=0;i<m;i++)
        {
    
            for(int j=0;j<n;j++)
            {
    
                 if(i>0&&j>0)
                {
    
                    dp[i][j]=min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
                }
                else if(i>0)
                {
    
                    dp[i][j]=dp[i-1][j]+grid[i][j];
                }
                else if(j>0){
    
                     dp[i][j]=dp[i][j-1]+grid[i][j];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

---

summary

In fact, dynamic problems only need to consider how to define the data structure 、 The meaning of structure 、 Establishment of state transition equation .
Most of the data structures are dp[i][j], It is difficult to define dp[i][j] The meaning of 、i The meaning of representation 、j The meaning of representation
State transition equation ： In fact, it's about thinking about changes ：dp[i][j] and dp[i-1][j]、dp[i][j-1] The relationship between , This needs to be analyzed according to the problem , Analyze through the results of the problem dp[i][j] How to get to the last step of dp[i][j], such as dp[i][j]–> arrive grid[i][j] The minimum sum of numbers ,dp[i-1][j]–> arrive grid[i-1][j] The minimum sum of numbers ,dp[i-1][j]–> arrive grid[i][j-1] The minimum sum of numbers , This is a recursive idea , You can't always think about how to find the smallest one step by step at the beginning , Instead, you just need to find out how to get from the last smallest to the next smallest , This is the idea of recursion .