Codeforces Round ＃804 (Div. 2)

题目链接

A  The Third Three Number Problem

题意

给你一个n，让你求满足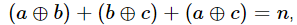的a，b，c。

 

如果不存在则输出-1.

思路

 显然任意a，b，c是不可能得到奇数。

只考虑偶数可以得到一个特殊构造 n/2 , 0 , 0 。

代码

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef long long ll;
const ll N = 1e6;
void solve()
{
    int n;
    cin >> n;
    if (n % 2 == 1)
        cout << "-1\n";
    else
        cout << n / 2 << " 0 0\n";
}
 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

 

B - Almost Ternary Matrix

题意

构造01矩阵，要求每个数的上下左右最多有两个数相同。

思路

以这个图案  为基本构造单元进行扩展，再根据题意所给的范围截出需要的图案。

 

代码

 

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef long long ll;
const ll N = 1e6;
int s[10][65];
void solve()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
            cout << s[i % 4][j] << " ";
        cout << endl;
    }
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    s[1][1] = 1, s[1][2] = 0, s[1][3] = 0, s[1][4] = 1;
    s[1][0] = 1;
    s[2][1] = 0, s[2][2] = 1, s[2][3] = 1, s[2][4] = 0;
    s[2][0] = 0;
    for (int i = 1; i <= 60; i++)
    {
        s[0][i] = s[1][i % 4];
        s[1][i] = s[1][i % 4];
        s[2][i] = s[2][i % 4];
        s[3][i] = s[2][i % 4];
    }
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}

 

 

C - The Third Problem

题意

给一个长为n的数组a，内容是0到n-1。定义一个操作MEX为集合c1,c2,.....,ck  中没有出现的最小非负数。

 例如

 

 让你求一个数组b，内容也是0到n-1。对任意 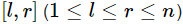都有

 

 

思路

设是s[x]为 x 在a 中的位置

首先考虑0的位置，因为MEX[0]=1,所以0的位置只能是s[0]，可以确定1的位置为s[1]。

接下来确定 2~n-1的方法相同，以 0 和 1 的索引确定区间 [L， R]，如果下一个 数x 的索在入区间 [L， R]，则更新ans为（（区间长度）-（x-1））*ans， 如果 k 的索引位于区间之外则更新L或R增加区间长度。

代码

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
typedef long long ll;
const ll N = 1e5, mod = 1e9 + 7;
void solve()
{
    int n;
    cin >> n;
    int sf[n];
    vector<int> s(n);
    for (int i = 0; i < n; i++)
    {
        cin >> sf[i];
        s[sf[i]] = i;
    }
    int l = s[0], r = s[0];
    ll ans = 1;
    for (int i = 1; i < n; i++)
    {
        if (s[i] > r)
            r = s[i];
        else if (s[i] < l)
            l = s[i];
        else
            ans = ans * (r - l + 1 - i) % mod;
    }
    cout << ans << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int t;
    cin >> t;
    while (t--)
        solve();
    return 0;
}