611. Number of effective triangles

611. The number of effective triangles

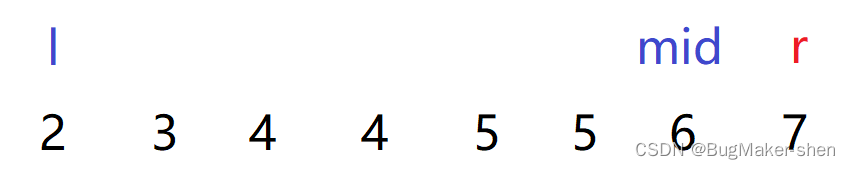
here $nums[l]+nums[mid]>nums[r]$,$l$ take $[l,mid-1]$ Any number in satisfies the condition , There are $ans+=(mid-l)$

Our current triple （2,6,7） The conditions are satisfied , Due to the inequality on the right nums[r] Fix , What we need to do is to adjust the size of the left side of the inequality , Try to satisfy the inequality

Because we let $l$ take $[l,mid-1]$ Any number within is an attempt to make the left side of the inequality larger （ Still meet the conditions ）, We should now make the left side of the inequality smaller , Continue to check whether the triangle condition is met , That is to move to the left mid, Continue looking for triples

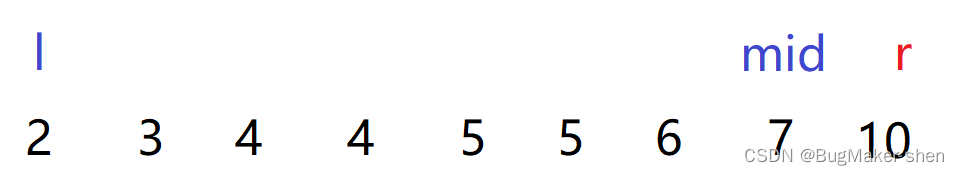
When the conditions are not met , The sum of two small numbers is too small , To make the left side of the inequality larger , There is only one choice ： To the right $l$ Take a larger number

class Solution {
    
public:
    int triangleNumber(vector<int>& nums) {
    
        sort(nums.begin(), nums.end(), less<int>());
        int n = nums.size();
        int ans = 0;
        //  Fix the maximum number in each cycle 
        for (int r = n - 1; r >= 2; r--){
    
            int l = 0;
            int mid = r - 1;
            while(l < mid){
    
                if(nums[l] + nums[mid] > nums[r]){
    
                    ans += (mid - l);
                    // mid It's from r-1 At the beginning ,mid The initial value is large , Now the triangle condition is satisfied , You need to find the number that meets the triangle condition among the smaller numbers 
                    mid--;
                }else{
    
                    //  The sum of two small numbers is too small 
                    l++;
                }
            }
        }
        return ans;
    }
};

Then we can fix the minimum value , use mid and r Looking for triples ？

In this case , Triangle condition is not satisfied , The sum of two small numbers is too small , We can adjust to the right $mid$ Give Way $nums[l]+nums[mid]$ It's worth more , Or left adjustment $r$, Give Way $nums[r]$ It's worth less , To satisfy the triangle inequality . This operation is more difficult ：

Let's adjust to the right mid,mid Point to 3, We will miss （2,2,3） This combination ; To the left r,r Point to 3, We will miss （2,3,4） This combination

So we should put two pointers for searching triples on the same side of the inequality , When triangle inequality is not satisfied, there is only one choice