当前位置:网站首页>Overview of three core areas of Mathematics: algebra
Overview of three core areas of Mathematics: algebra
2022-07-06 06:02:00 【Zhan Miao】
Mathematics has developed to the present , It has become owned in the scientific world 100 A large number of major sub disciplines “ republic ”. Generally speaking, mathematics has three core areas :
The part of mathematics that studies numbers belongs to the category of algebra ;
Study the part of form , It belongs to the fan Chou of geometry ;
The part that communicates form and number and involves limit operation , It belongs to the scope of analysis .
These three kinds of mathematics constitute the ontology and core of the whole mathematics . Around this core , Because mathematics passes the two concepts of number and shape , Permeate with other sciences , And there are many marginal and interdisciplinary disciplines . This paper briefly introduces the historical development of more than ten main branches of mathematics in the three core fields .
1. The arithmetic
Arithmetic has two meanings , One is handed down from China , Equivalent to what is generally said “ mathematics ”, Such as 《 Nine chapters on arithmetic 》 etc. . The other is translated from European Mathematics , From Greek , Yes “ Computing technology ” The meaning of . Now generally speaking “ The arithmetic ”, It often refers to the four operations of natural numbers ; If it is in Higher Mathematics , Then there are “ number theory ” The meaning of . Arithmetic as the content of modern primary school curriculum , It mainly talks about natural numbers 、 Positive fractions and their four operations , And it is consolidated by some of the simplest application problems caused by counting and measurement .

Arithmetic is the oldest branch of Mathematics , Some of its conclusions are that for thousands of years , Slowly and gradually established . They reflect the accumulation over many centuries , And constantly solidify the experience in people's consciousness .
Natural numbers are in the process of calculating a finite set of objects , The resulting abstract concepts . In daily life, people are required not only to calculate a single object , Also calculate various quantities , For example, length 、 Weight and time . To meet these simple measurement needs , Scores are needed .
The development of modern elementary arithmetic operation methods , It originated in India , The time may be 10 Century or 11 century . It was later adopted by Arabs , Then it spread to Western Europe .15 century , It was transformed into its present form . After Indian arithmetic , Obviously, there is the influence of ancient China .
19 In the middle of the century , Glassman successfully selected a basic axiom system for the first time , To define addition and multiplication ; And other propositions of arithmetic , It can be the result of logic , Derived from this system . later , Piano further improved Glassman's system .
Basic concepts of arithmetic and rules of logical inference , Based on human practical activities , It profoundly reflects the objective regularity of the world . Although it is highly abstract , But because the raw materials it summarizes are so extensive , So we can hardly leave it . meanwhile , It also constitutes the most solid foundation for other branches of Mathematics .
2. Elementary algebra
Elementary algebra, as the main content of middle school mathematics curriculum , Its central content is equation theory . The Latin original meaning of algebra is “ place ”. The theory of algebraic equations in elementary algebra is extended from univariate linear equations to two aspects : One is to increase the number of unknowns , Consider a system of binary or ternary equations consisting of several equations with several unknowns ( It is mainly a system of first-order equations ); The second is to increase the number of unknowns , Investigate the univariate quadratic equation or quasi quadratic equation . The main content of elementary algebra is 16 The century has been basically developed .
Babylon, Cuba ( B.c. 19 century ~ front 17 century ) Solve the problem of first and second order equations , Euclidean 《 Original 》( B.c. 4 century ) There is a method of solving quadratic equations in geometric form . Our country 《 Nine chapters on arithmetic 》( A.D. 1 century ) There are solutions of cubic equations and first-order simultaneous equations , And uses negative numbers .3 Diophantine of the th century is calculated once with rational numbers 、 Solutions of quadratic indefinite equations .13 Tianyuan technique appeared in China in the th century ( Li Ye 《 Round sea mirror 》) It is about the numerical solution of higher-order equations in one variable .16 In the th century, Italian mathematicians discovered the solution of cubic and quartic equations .
The history of the development of algebraic symbols , It can be divided into three stages . The first stage was three centuries ago , There is no abbreviation or symbol for the solution of the problem , Instead, write a paper , It is called literal narrative algebra . The second stage is from the third century to 16 century , Abbreviations are used for some common quantities and operations , It is called simplified algebra . One of the outstanding contributions of tifantu in the third century , Is to simplify Greek algebra , Pioneered simplified algebra . However, since then, text narrative algebra , In other parts of the world except India , It has been very common for hundreds of years , Especially in Western Europe until 15 century . The third stage is 16 After the century , The solution to the problem is mostly expressed in mathematical shorthand composed of symbols , These symbols have no obvious connection with the content they represent , It is called symbolic algebra .16 Weida's masterpiece in the century 《 Introduction to analytical methods 》, He has made many contributions to the development of symbolic algebra .16 The end of the century , Vyte pioneered symbolic algebra , It has become a modern form after Descartes' improvement .
“+”、“-” No. 1 first appeared in a math book , yes 1489 Weidman's work in . But officially recognized by everyone , As a plus 、 The sign of subtraction , That's from 1514 Started by Hoek in .1540 year , Recod started using it now “=”. To 1591 year , After Veda's extensive use in his works , It is gradually accepted by people .1600 Harryott created the greater than sign “>” And the less than sign “<”.1631 year , Autre gives “×”、“÷” As a multiplication and division operator .1637 year , Descartes used the root sign for the first time , And introduce the letters in front of the alphabet to represent known numbers 、 The following letters indicate the custom of unknown numbers . as for “≮”、“≯”、“≠” The appearance of these three symbols , That's a modern thing .
Extension of the concept of number , In history, it is not all caused by solving algebraic equations , But it is still used to put it in elementary algebra , In order to be consistent with the arrangement of this course . B.c. 4 century , The ancient Greeks discovered irrational numbers . B.c. 2 century ( In the Western Han Dynasty ), China began to use negative numbers .1545 year , Cardano of Italy began to use imaginary numbers .1614 year , Britain's nipple invented logarithm .17 The end of the century , The general concept of real number index is gradually formed .
3. Advanced algebra


In Higher Algebra , First order equations ( Linear equations ) Developed into linear algebra theory ; and —、 Quadratic equations developed into polynomial theory . The former is vector space 、 linear transformation 、 Type theory 、 Invariant theory and tensor algebra, a branch of modern algebra , The latter is a branch of modern algebra that studies equations of any degree with only one unknown quantity . Advanced algebra as a college course , Only study their basis .
1683 Nian guanxiaohe ( The Japanese ) The concept of determinant was first introduced . The most systematic discussion about Determinant Theory , Jacobi 1841 Year of 《 On the formation and nature of determinant 》 A Book . Logically , The concept of matrix precedes the concept of determinant ; And in history , The order is just the opposite . Carlyle is 1855 In, the concept of matrix was introduced , stay 1858 In, he published the first important article on this subject 《 Research Report of matrix theory 》.
19 century , Determinants and matrices have received great attention , There have been more than a thousand articles on these two topics . however , They are not big reforms in Mathematics , It's an expression of shorthand . However, they have proved to be highly useful tools .
The study of polynomial algebra began with 3、4 Exploration of the formula for finding the root of sub equation .1515 year , Filo solved the problem of being simplified to lack 2 Secondary 3 The problem of solving sub equation .1540 year , Ferrari succeeded in discovering the general 4 Algebraic solution of sub equation . People continue to seek 5 Time 、6 The formula for finding the root of an equation of degree or higher , But these efforts are 200 It has been lost for many years .
1746 year , D'Alembert first gave “ The fundamental theorem of algebra ” The proof of ( There are imperfections ). This theorem asserts : For each real coefficient or complex coefficient n Subalgebral equation , At least one solid root or compound root . therefore , Generally speaking ,n Subalgebral equations should have n A root .1799 year ,22 Gauss is writing his doctoral thesis , The first strict proof of this theorem is given .1824 year ,22 Year old Abel proved : higher than 4 The radical formula composed of all the coefficients of the general equation of degree , It can't be its root .1828 year , Years old 17 Galois, aged, founded “ Galois theory ”, It includes the necessary and sufficient conditions for the equation to be solved with the root sign .
4. number theory
Number theory with positive integers as its research object , It can be seen as part of arithmetic , But it is not from an operational point of view , But from the point of view of the structure of numbers , That is, a number can be expressed by other numbers with simpler properties . So we can say , Number theory is the science of studying the number system composed of integers in a certain form .

As early as BC 3 century , Euclidean 《 Original 》 Some properties of integers are discussed . He proved that the number of primes is infinite , He also gave a toss and turn division method for finding the common divisor of two numbers . This has nothing to do with our country 《 Nine chapters on arithmetic 》 Medium “ More derogation ” It's the same . Eratoseni gave the idea of finding a natural number no greater than a given number N All primes of “ Sieve method ”: In writing from 1 To N On the papyrus of all integers , Dig out in turn 2、3、5、7…… Multiple ( Respective 2 times ,3 times ,……) as well as 1, All that is left on this sieve of papyrus is prime .

When the difference between two integers can be positive integers m Except when , Call these two numbers for “ model ”m congruence . In our country 《 Sun Tzu's Sutra 》( A.D. 4 century ) Calculate the group of primary congruences in “ Seek a skill ”, Yes “ Chinese remainder theorem ” Known as the .13 century , Qin Jiushao has established a relatively complete congruence theory ——“ Da Yan seeks a technique ”, This is one of the contents of number theory .
Throwing pictures 《 The arithmetic 》 The solution is given in x?+y?=z? All integer solutions . Ferma points out x^n+y^n=z^n stay n>3 There is no integer solution , The research on this problem has produced 19 Number theory of the century . Then Gauss 《 Number theory research 》(1801 year ) Formed a systematic number theory .
The classical content of number theory basically does not rely on the methods of other branches of Mathematics , It is called elementary number theory .17 After the middle of the century , Algebra developed under the influence of number theory 、 The geometric 、 analysis 、 Branches of mathematics such as probability , In turn, it promoted the development of number theory , Algebraic number theory appeared ( Study the roots of polynomials with integral coefficients —“ Algebraic number ”)、 Geometric number theory ( Study all coordinates that are integers in the linear coordinate system “ On the hour ”—“ Space grid ”).19 Analytic number theory appeared in the second half of the century , Study the distribution of prime numbers by analytical methods . In the 20th century, complete number theory appeared .
5. Abstract algebra
1843 year , Hamilton invented an algebra in which the commutative law of multiplication does not hold —— Quaternion algebra . In the second year , Glassman deduces several more general types of algebra .1857 year , Carlyle designed another kind of non commutative algebra —— Matrix algebra . Their research opened up abstract algebra ( Also called modern algebra ) Gate . actually , Weaken or delete some assumptions of ordinary algebra , Or replace some assumptions with other assumptions ( Compatible with other assumptions ), You can study many algebraic systems .
1870 year , Clonic gives the abstract definition of finite Abelian group ; Didkin began to use “ body ” That's what I'm saying , And we study algebras ;1893 year , Weber defined abstract body ;1910 year , Stannitz developed the general abstract theory of body ; Didkin and clonic founded ring theory ;1910 year , Stannitz summed up the inclusion Group 、 Algebra. 、 Study of algebraic systems including fields , Created abstract algebra .
1926 year , Nott achieved his ideal ( Count ) theory ;1930 year , Bilhoff established lattice theory , It comes from 1847 Boolean algebra of ; After the Second World War , There have been theories of various algebraic systems and the bulbaki School ;1955 year , Jiadang 、 Glucindick and ellenburger established homology algebra theory .
Up to now , Mathematicians have studied 200 There are many such algebraic structures , Among them, the most important derodan algebras and Lie algebras are examples of algebras that do not obey the law of Association . Most of these jobs belong to 20 century , They make the thoughts of generalization and abstraction fully reflected in Modern Mathematics .
Abstract algebra is a mathematical discipline that studies various abstract axiomatic algebraic systems . Typical algebraic systems have groups 、 Ring 、 Domain etc , They mainly originated from 19 Group theory of the century , Including group theory 、 Ring theory 、 Galois theory 、 Case theory 、 Linear algebra and many other branches , Combined with other branches of mathematics, algebraic geometry 、 Algebraic number theory 、 Algebraic topology 、 Topological groups and other new mathematical disciplines . Abstract algebra has become the universal language of most contemporary mathematics .
Now? , Algebra can be generally interpreted as the theory of letter calculation , But the meaning of letters is constantly expanding . In elementary algebra , Letters indicate numbers ; In Higher Algebra and abstract algebra , Letters represent vectors ( or n Meta ordered array )、 matrix 、 tensor 、 Spinor 、 Hypercomplex and other forms of quantity . so to speak , Algebra has developed into a general theory of formal operations .
边栏推荐
- Clear floating mode
- Investment strategy discussion and market scale prediction report of China's solid state high power amplifier industry from 2022 to 2028
- H3C V7 switch configuration IRF
- First knowledge database
- Linux regularly backs up MySQL database
- Is it difficult for an information system project manager?
- Hongliao Technology: how to quickly improve Tiktok store
- Analysis of grammar elements in turtle Library
- Classes and objects (I) detailed explanation of this pointer
- Software test interview questions - Test Type
猜你喜欢

A master in the field of software architecture -- Reading Notes of the beauty of Architecture
Embedded point test of app
![Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)](/img/c9/56fba6054c91f090de31463a8b4705.jpg)
Buuctf-[bjdctf2020]zjctf, but so (xiaoyute detailed explanation)
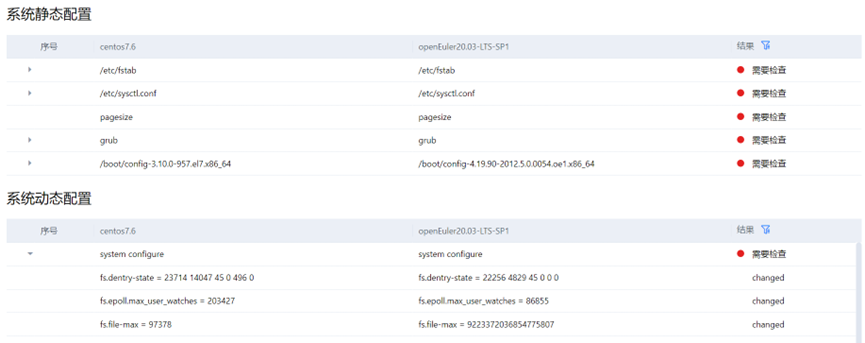
实践分享:如何安全快速地从 Centos迁移到openEuler
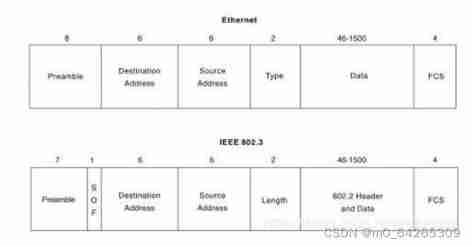
IP day 16 VLAN MPLS configuration

Report on the competition status and investment decision recommendations of Guangxi hospital industry in China from 2022 to 2028

Wib3.0 leapfrogging, in leapfrogging (ง • ̀_•́) ง
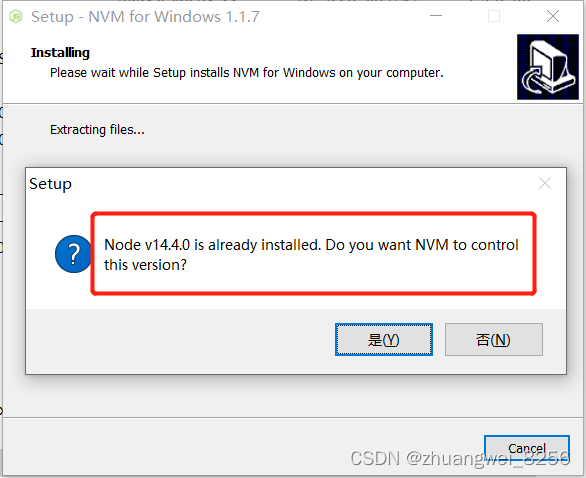
Node 之 nvm 下载、安装、使用,以及node 、nrm 的相关使用
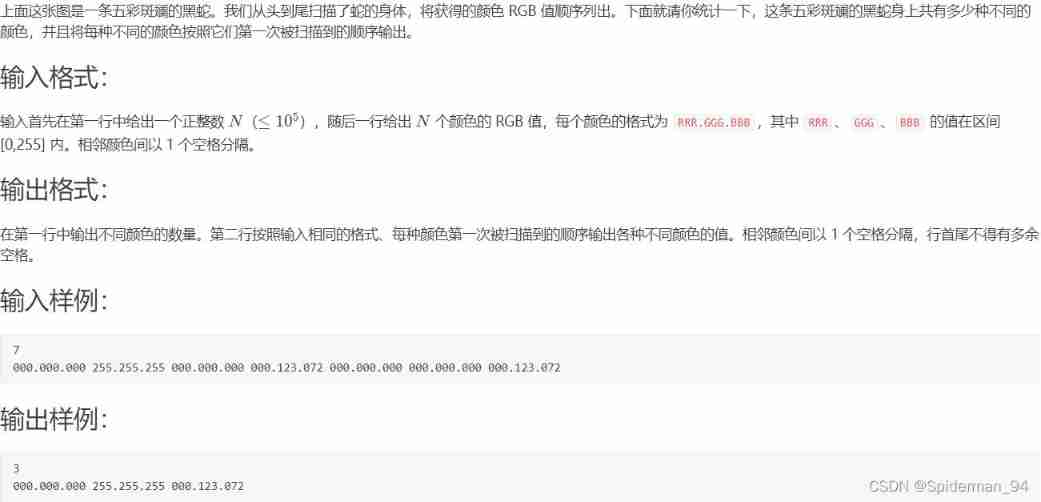
Winter 2021 pat class B problem solution (C language)
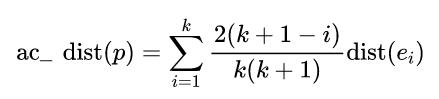
异常检测方法总结
随机推荐
Station B, Mr. Liu Er - multiple logistic regression, structure 7
c语言——冒泡排序
Jushan database appears again in the gold fair to jointly build a new era of digital economy
Go language -- language constants
Baidu online AI competition - image processing challenge: the 8th program of handwriting erasure
Report on the competition status and investment decision recommendations of Guangxi hospital industry in China from 2022 to 2028
Is it difficult for an information system project manager?
P2802 go home
请求转发与重定向
isam2运行流程
Investment strategy discussion and market scale prediction report of China's solid state high power amplifier industry from 2022 to 2028
Yygh-11-timing statistics
Processes and threads
ContentType的作用
nodejs实现微博第三方登录
查询生产订单中某个(些)工作中心对应的标准文本码
AUTOSAR from getting started to becoming proficient (10) - embedded S19 file analysis
Request forwarding and redirection
误差的基本知识
养了只小猫咪