当前位置:网站首页>Understanding of maximum likelihood estimation
Understanding of maximum likelihood estimation
2022-07-08 01:23:00 【You roll, I don't roll】
Maximum likelihood estimation It's based on Maximum likelihood principle A statistical method based on , It's the application of probability theory in statistics .
Catalog
1、 Maximum likelihood principle
2、 Maximum likelihood estimation
1、 Maximum likelihood principle
Maximum likelihood principle : In a randomized trial , Many events can happen , The probability of an event with a high probability is also high . If only one test is conducted , event A It happened. , Then we have reason to think A The probability of occurrence is higher than that of other events .
for example , There is... In a box red black Two color balls , The number of 10 And 1 individual , But I don't know which color ball is 10 A ball of that color is 1 individual , At this time, we randomly take out a ball from the box , If this ball is red Chromatic , Then we think it's in the box red Ball has 10 individual , black Ball has 1 individual .
2、 Maximum likelihood estimation
Maximum likelihood estimation (ML) Is to use the known sample results ( For example, the ball touched in the above example is red Chromatic ), Backward extrapolation is most likely ( Maximum probability ) The parameter value that causes this result ( As shown in the above example 10 red 1 black Conclusion ). This is also in Statistics Estimate the whole with samples An elaboration of .
ML A method for evaluating model parameters given observation data is provided , namely :“ The model has been set , Unknown parameter ”. Through several experiments , Observe the results , Using the test results to get a certain parameter value can make the probability of sample occurrence to be the maximum , It's called maximum likelihood estimation .
How to understand “ The model has been set , Unknown parameter ” Well ? The model here can be a Formula with undetermined parameters , It can also be thought of as a Machine learning model .
Such as exponential distribution formula
The distribution function model is known , Parameters λ That is, the required parameter , Given a set of random variables D, Find the most appropriate parameter
Under this parameter D The probability of occurrence is the highest .
Another example is , We have a model , The unknown parameters in the model are ![]() , The value range is
, The value range is ![]() . Another group contains N The data set of 2 samples D:
. Another group contains N The data set of 2 samples D:
![]()
We require a set of parameters of the model ![]() , Make the data set D The probability of occurrence is the greatest . Definition Likelihood function ( Data sets D Probability of occurrence ) as follows :
, Make the data set D The probability of occurrence is the greatest . Definition Likelihood function ( Data sets D Probability of occurrence ) as follows :
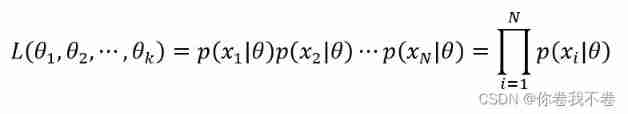
To solve the likelihood function is to find a set of parameters ![]() bring
bring ![]() To the maximum , here
To the maximum , here ![]() Namely
Namely ![]() Maximum likelihood estimator of .
Maximum likelihood estimator of .
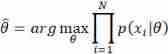
Find the maximum , Which must involve function derivation , But look at L We know that the direct derivation process may be very troublesome and the order of the result is high , And consider the function ln(L) And L Have the same trend and maximum point , Therefore, in practical application, in order to facilitate analysis , Generally used Log likelihood function H=ln(L) To solve ![]() .
.
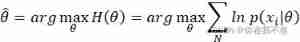
And then make it Partial derivative be equal to 0:
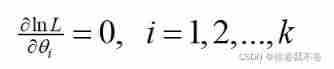
The solution of the equation is only an estimate , Only when the number of samples tends to be infinite , It will be close to the real value .
Reference resources :
Wu Chuansheng :《 Economic Mathematics - Probability theory and mathematical statistics 》
边栏推荐
- USB type-C docking design | design USB type-C docking scheme | USB type-C docking circuit reference
- C# ?,?.,?? .....
- Probability distribution
- 2021 welder (primary) examination skills and welder (primary) operation examination question bank
- General configuration tooltip
- Kuntai ch7511b scheme design | ch7511b design EDP to LVDS data | pin to pin replaces ch7511b circuit design
- The whole life cycle of commodity design can be included in the scope of industrial Internet
- swift获取url参数
- Content of one frame
- Frrouting BGP protocol learning
猜你喜欢
Basic implementation of pie chart
130. Surrounding area

How to use education discounts to open Apple Music members for 5 yuan / month and realize member sharing
Chapter 7 Bayesian classifier
Running OFDM in gnuradio_ RX error: gr:: Log: info: packet_ headerparser_ b0 - Detected an invalid packet at item ××
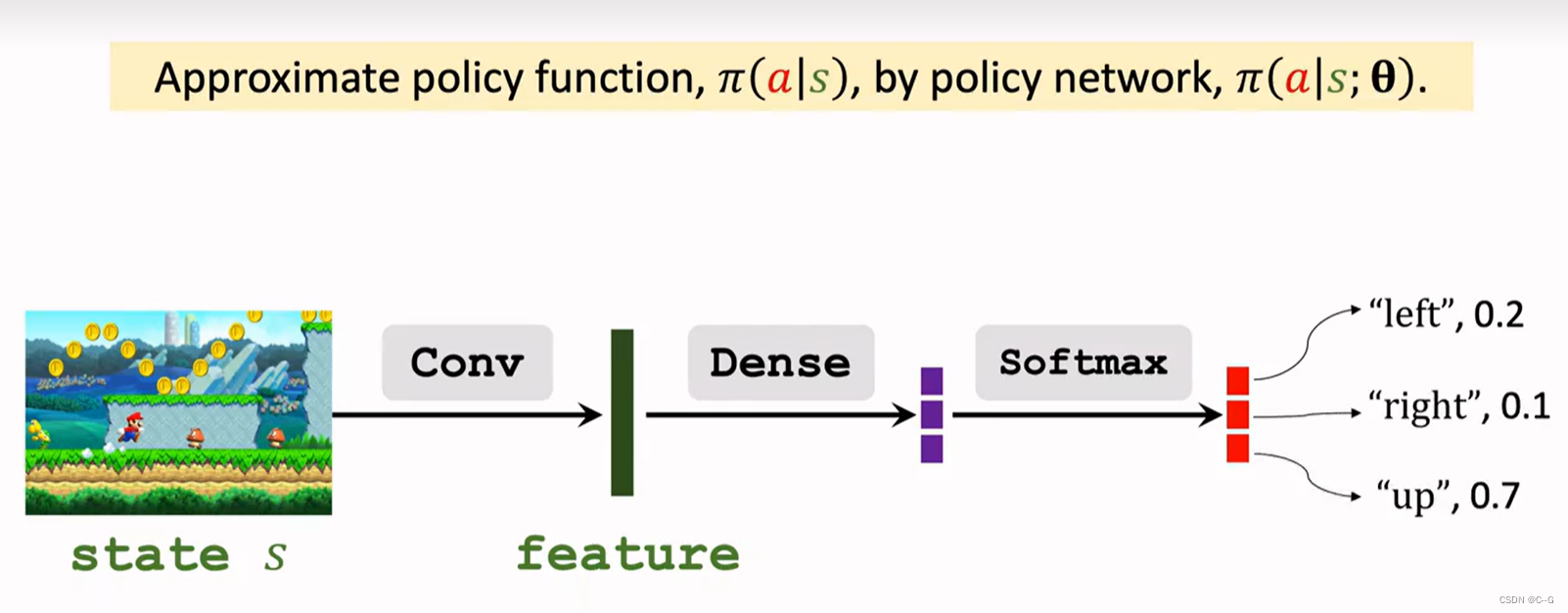
4. Strategic Learning

For the first time in China, three Tsinghua Yaoban undergraduates won the stoc best student thesis award

Vscode reading Notepad Chinese display garbled code
Led serial communication

4、策略學習
随机推荐
Understanding of sidelobe cancellation
Get started quickly using the local testing tool postman
y59.第三章 Kubernetes从入门到精通 -- 持续集成与部署(三二)
Serial port receives a packet of data
Share a latex online editor | with latex common templates
2022 low voltage electrician examination content and low voltage electrician simulation examination question bank
5、離散控制與連續控制
Ag9310meq ag9310mfq angle two USB type C to HDMI audio and video data conversion function chips parameter difference and design circuit reference
133. 克隆图
【深度学习】AI一键换天
EDP to LVDS conversion design circuit | EDP to LVDS adapter board circuit | capstone/cs5211 chip circuit schematic reference
Cross modal semantic association alignment retrieval - image text matching
130. Zones environnantes
The beauty of Mathematics -- the principle of fine Fourier transform
General configuration tooltip
FIR filter of IQ signal after AD phase discrimination
Leetcode notes No.21
Basic implementation of pie chart
Leetcode notes No.7
Redis集群