当前位置:网站首页>闇の連鎖(LCA+树上差分)
闇の連鎖(LCA+树上差分)
2022-07-06 09:18:00 【小陈同学_】
题目
传说中的暗之连锁被人们称为 D a r k Dark Dark。
D a r k Dark Dark 是人类内心的黑暗的产物,古今中外的勇者们都试图打倒它。
经过研究,你发现 D a r k Dark Dark 呈现无向图的结构,图中有 N N N 个节点和两类边,一类边被称为主要边,而另一类被称为附加边。
D a r k Dark Dark 有 N – 1 N–1 N–1 条主要边,并且 D a r k Dark Dark 的任意两个节点之间都存在一条只由主要边构成的路径。
另外, D a r k Dark Dark 还有 M M M 条附加边。
你的任务是把 D a r k Dark Dark 斩为不连通的两部分。
一开始 D a r k Dark Dark 的附加边都处于无敌状态,你只能选择一条主要边切断。
一旦你切断了一条主要边, D a r k Dark Dark 就会进入防御模式,主要边会变为无敌的而附加边可以被切断。
但是你的能力只能再切断 D a r k Dark Dark 的一条附加边。
现在你想要知道,一共有多少种方案可以击败 D a r k Dark Dark。
注意,就算你第一步切断主要边之后就已经把 D a r k Dark Dark 斩为两截,你也需要切断一条附加边才算击败了 D a r k Dark Dark。
输入格式
第一行包含两个整数 N N N 和 M M M。
之后 N – 1 N–1 N–1 行,每行包括两个整数 A A A 和 B B B,表示 A A A 和 B B B 之间有一条主要边。
之后 M M M 行以同样的格式给出附加边。
输出格式
输出一个整数表示答案。
数据范围
N ≤ 100000 N≤100000 N≤100000, M ≤ 200000 M≤200000 M≤200000,数据保证答案不超过 2 31 − 1 2^{31}−1 231−1
输入样例:
4 1
1 2
2 3
1 4
3 4
输出样例:
3
LCA+树上差分
该题目是让我们删掉一条主要边和一条附加边将图变为两部分
1. 由 于 给 出 的 图 有 n 个 点 、 n − 1 条 主 要 边 、 m 条 附 加 边 并 且 任 意 两 点 之 间 都 由 主 要 边 相 连 , 说 明 该 图 是 由 主 要 边 构 成 的 一 棵 树 1.由于给出的图有n个点、n-1条主要边、m条附加边并且任意两点之间都由主要边相连,说明该图是由主要边构成的一棵树 1.由于给出的图有n个点、n−1条主要边、m条附加边并且任意两点之间都由主要边相连,说明该图是由主要边构成的一棵树
2. x 到 y 的 路 径 中 的 附 加 边 < = 1 才 可 以 把 图 变 成 两 部 分 ( 为 什 么 ? : 因 为 主 要 边 已 经 构 成 了 一 颗 树 , 如 果 某 两 点 路 径 中 存 在 一 条 以 上 的 附 加 边 , 则 说 明 删 掉 一 条 附 加 边 , 其 他 地 方 还 是 连 通 的 , 就 不 能 把 图 变 为 两 部 分 ) 2.x到y的路径中的附加边<=1才可以把图变成两部分(为什么?:因为主要边已经构成了一颗树,如果某两点路径中存在一条以上的附加边,则说明删掉一条附加边,其他地方还是连通的,就不能把图变为两部分) 2.x到y的路径中的附加边<=1才可以把图变成两部分(为什么?:因为主要边已经构成了一颗树,如果某两点路径中存在一条以上的附加边,则说明删掉一条附加边,其他地方还是连通的,就不能把图变为两部分)
3. 需 要 统 计 该 路 径 中 有 多 少 条 附 加 边 。 该 如 何 来 处 理 路 径 中 附 加 边 的 个 数 呢 ? — > 树 上 差 分 3.需要统计该路径中有多少条附加边。该如何来处理路径中附加边的个数呢?—>树上差分 3.需要统计该路径中有多少条附加边。该如何来处理路径中附加边的个数呢?—>树上差分
4. 树 上 差 分 : 如 果 想 让 x 和 y 之 间 的 路 径 上 加 上 一 个 数 c 并 且 不 影 响 其 他 路 径 的 结 果 : x + = c , y + = c , l c a ( x , y ) − = 2 ∗ c 。 【 l c a ( x , y ) 是 x 和 y 的 最 近 公 共 祖 先 】 4.树上差分:如果想让x和y之间的路径上加上一个数c并且不影响其他路径的结果:x+=c,y+=c,lca(x,y)-=2*c。【lca(x,y)是x和y的最近公共祖先】 4.树上差分:如果想让x和y之间的路径上加上一个数c并且不影响其他路径的结果:x+=c,y+=c,lca(x,y)−=2∗c。【lca(x,y)是x和y的最近公共祖先】
5. 三 种 情 况 : ( 路 径 中 权 值 用 d 来 表 示 、 a n s 代 表 答 案 ) 5.三种情况:(路径中权值用d来表示、ans代表答案) 5.三种情况:(路径中权值用d来表示、ans代表答案)
(1)d=0:砍掉主要边之后,无论砍掉哪条附加边,图还是两部分,所以有m中方案—>ans+=m;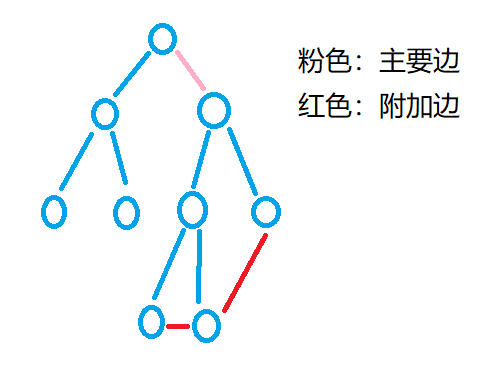
(2)d=1:砍掉主要边之后,必须要砍掉该附加边才可以使图变为两部分,所以只有一种方案—>ans++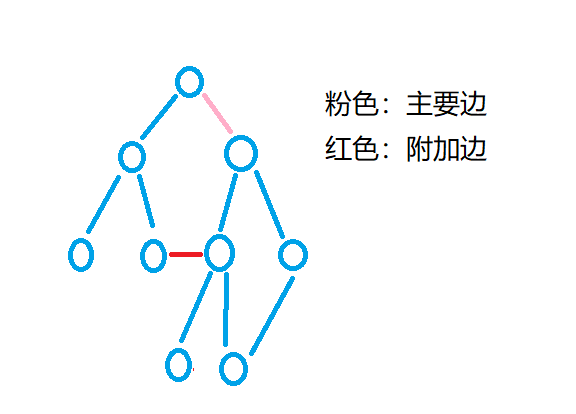
(3)d>=2:砍掉主要边之后,无论砍掉哪条附加边也不能将图变为两部分,所以此方案是不可行的—>ans+=0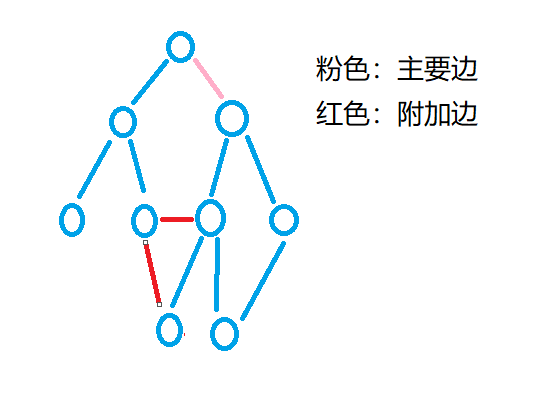
AC代码(C++)
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
using namespace std;
const int N=100010,M=N<<1;
int depth[N]; //每一个点的深度
bool st[N];
int n,m;
int f[N][20]; //f[i][j]:i点跳j次所到的点
int h[N],e[M],ne[M],idx;
int s[N]; //前缀和
int ans;
void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
//预处理每个点的深度和每个点跳k次能跳到的点
void bfs(){
queue<int> q;
memset(depth,0x3f,sizeof depth);
depth[0]=0,depth[1]=1;
q.push(1);
st[1]=true;
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(depth[j]>depth[t]+1){
depth[j]=depth[t]+1;
f[j][0]=t;
for(int k=1;k<=16;k++){
f[j][k]=f[f[j][k-1]][k-1];
}
if(!st[j]){
st[j]=true;
q.push(j);
}
}
}
}
}
//最近公共祖先
int lca(int a,int b){
if(depth[a]<depth[b]) swap(a,b);
//不同深度
for(int k=16;k>=0;k--){
if(depth[f[a][k]]>=depth[b]){
a=f[a][k];
}
}
if(a==b) return a;
//如果上面没有返回,那就说明a和b已在同一层
for(int k=16;k>=0;k--){
if(f[a][k]!=f[b][k]){
a=f[a][k];
b=f[b][k];
}
}
return f[a][0]; //此时a和b没有到最近公共祖先,需要在跳一次
}
int dfs(int u,int fa){
int res=s[u];
for(int i=h[u];i!=-1;i=ne[i]){
int j=e[i];
if(j==fa) continue;
int t=dfs(j,u);
if(t==0) ans+=m;
else if(t==1) ans++;
res+=t;
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
memset(h,-1,sizeof h);
for(int i=1;i<n;i++){
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
}
bfs();
for(int i=1;i<=m;i++){
int a,b;
scanf("%d%d",&a,&b);
int t=lca(a,b);
s[a]++,s[b]++,s[t]-=2;
}
dfs(1,-1);
printf("%d",ans);
return 0;
}
边栏推荐
- Force buckle 1189 Maximum number of "balloons"
- By v$rman_ backup_ job_ Oracle "bug" caused by details
- FairyGUI人物状态弹窗
- 服务未正常关闭导致端口被占用
- (3) Introduction to bioinformatics of R language - function, data Frame, simple DNA reading and analysis
- Acwing-116 pilot brother
- 音乐播放(Toggle && PlayerPrefs)
- Expected value (EV)
- (4) Data visualization of R language -- matrix chart, histogram, pie chart, scatter chart, linear regression and strip chart
- [offer9]用两个栈实现队列
猜你喜欢
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan

FairyGUI条子家族(滚动条,滑动条,进度条)

The master of double non planning left the real estate company and became a programmer with an annual salary of 25W. There are too many life choices at the age of 25

服务未正常关闭导致端口被占用

Latex learning
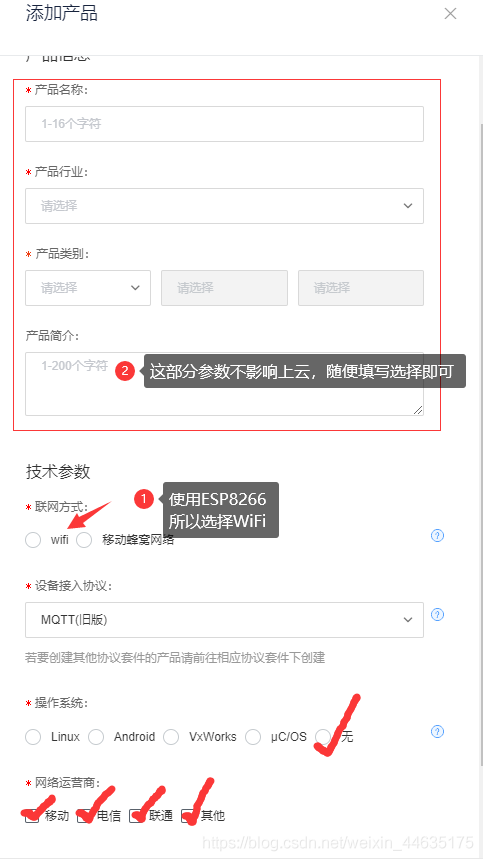
Esp8266 connect onenet (old mqtt mode)
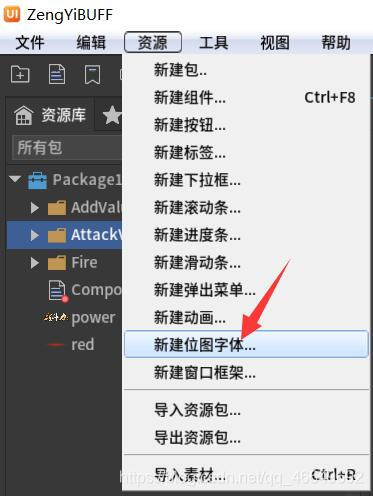
Fairygui gain buff value change display
Prove the time complexity of heap sorting
Teach you to release a DeNO module hand in hand
微信小程序开发心得
随机推荐
[算法] 剑指offer2 golang 面试题5:单词长度的最大乘积
Fairygui loop list
Database course design: college educational administration management system (including code)
(3) Introduction to bioinformatics of R language - function, data Frame, simple DNA reading and analysis
[leetcode15] sum of three numbers
(the first set of course design) 1-4 message passing interface (100 points) (simulation: thread)
Latex learning
Remember an experience of ECS being blown up by passwords - closing a small black house, changing passwords, and changing ports
Halcon knowledge: gray_ Tophat transform and bottom cap transform
Particle system for introduction to unity3d Foundation (attribute introduction + case production of flame particle system)
Unity3D制作注册登录界面,并实现场景跳转
Flink late data processing (3)
@The difference between Autowired and @resource
idea中导包方法
音乐播放(Toggle && PlayerPrefs)
MySQL performance tuning - dirty page refresh
基本Dos命令
In 2020, the average salary of IT industry exceeded 170000, ranking first
FairyGUI条子家族(滚动条,滑动条,进度条)
【GNSS】抗差估计(稳健估计)原理及程序实现