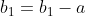1. Linear regression

The code running platform is jupyter-notebook, Code blocks in the article , According to jupyter-notebook Written in the order of division in , Run article code , Glue directly into jupyter-notebook that will do .

1. Import third-party library

import keras
import numpy as np
import matplotlib.pyplot as plt
# Sequential  Sequential model 
from keras.models import Sequential
# Dense  Fully connected layer 
from keras.layers import Dense

2. Randomly generate data sets

#  Use numpy Generate 100 A random point 
x_data = np.random.rand(100)
#  Noise shape and x_data The shape of is the same 
noise = np.random.normal(0,0.01,x_data.shape)
#  Set up w=0.1 b=0.2 
y_data = x_data*0.1+0.2+noise
# y_data_no_noisy = x_data*0.1+0.2
#  Show random points 
plt.scatter(x_data,y_data)
# plt.scatter(x_data,y_data_no_noisy)

Running effect ：
This is the case of adding noise y_data = x_data*0.1+0.2+noise：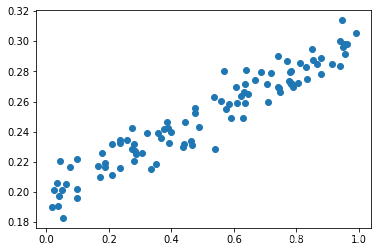

Without adding noise y_data_no_noisy = x_data*0.1+0.2（w=0.1,b=0.2）：

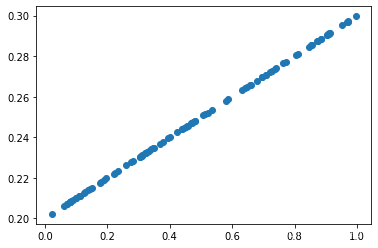
Linear regression is based on the scatter plot with added noise , Fit a straight line that is similar to the scatter diagram without adding noise .

3. Linear regression

#  Build a sequential model 
model = Sequential()
#  Add a full connection layer to the model   stay jupyter-notebook in , Press shift+tab Parameters can be displayed 
model.add(Dense(units=1,input_dim=1))
# sgd:Stochastic gradient descent ,  Random gradient descent method 
# mse:Mean Squared Error ,  Mean square error 
model.compile(optimizer='sgd',loss='mse')

#  Training 3001 Lots 
for step in range(3001):
    #  One batch at a time   The loss of 
    cost = model.train_on_batch(x_data,y_data)
    #  Every time 500 individual batch Print once cost
    if step%500==0:
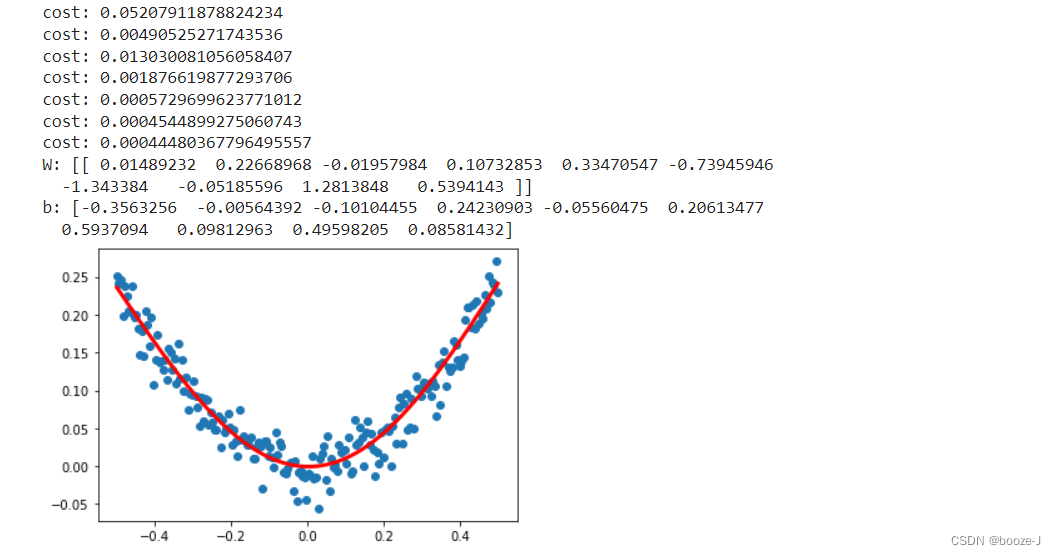
        print("cost:",cost)

#  Print weights and batch values 
W,b = model.layers[0].get_weights()
print("W:",W)
print("b:",b)

# x_data Input the predicted value in the network 
y_pred = model.predict(x_data)

#  Show random points 
plt.scatter(x_data,y_data)
#  Show forecast results 
plt.plot(x_data,y_pred,"r-",lw=3)
plt.show()

Running effect ：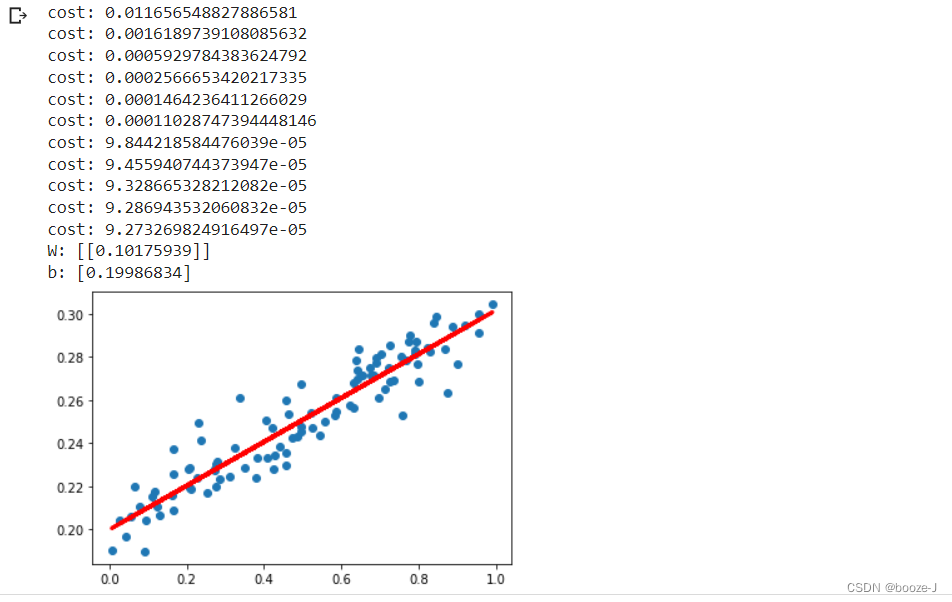

You can see the prediction w and b Are very close to what we set w and b.

Be careful

• stay jupyter-notebook in , Press shift+tab Parameters can be displayed
• train_on_batch Use
• compile Use