当前位置:网站首页>LeetCode:221. 最大正方形
LeetCode:221. 最大正方形
2022-07-06 08:44:00 【Bertil】
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
示例 1:
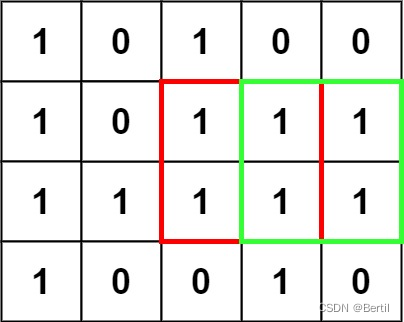
输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:
输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 300
- matrix[i][j] 为 ‘0’ 或 ‘1’
解题思路
1.首先定义一个数组dp表示以[i][j]为正方形右下角的最大边长,定义一个变量max_len表示最大正方形的边长
2.状态转移方程:dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;(取三者的最小值是因为要构成正方形)
3.注意:若左边和上边的点为’1’,则dp[i][j] = 1
代码
/** * @param {character[][]} matrix * @return {number} */
var maximalSquare = function(matrix) {
let max_len = 0;
let dp = Array.from(Array(matrix.length), () => Array(matrix[0].length).fill(0));
for (let i = 0; i < matrix.length; i++) {
for (let j = 0; j < matrix[i].length; j++) {
if (matrix[i][j] === '1') {
if (i === 0 || j === 0) {
dp[i][j] = 1;
}else {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;
}
max_len = Math.max(max_len, dp[i][j]);
}
}
}
return max_len ** 2;
};
边栏推荐
- JVM quick start
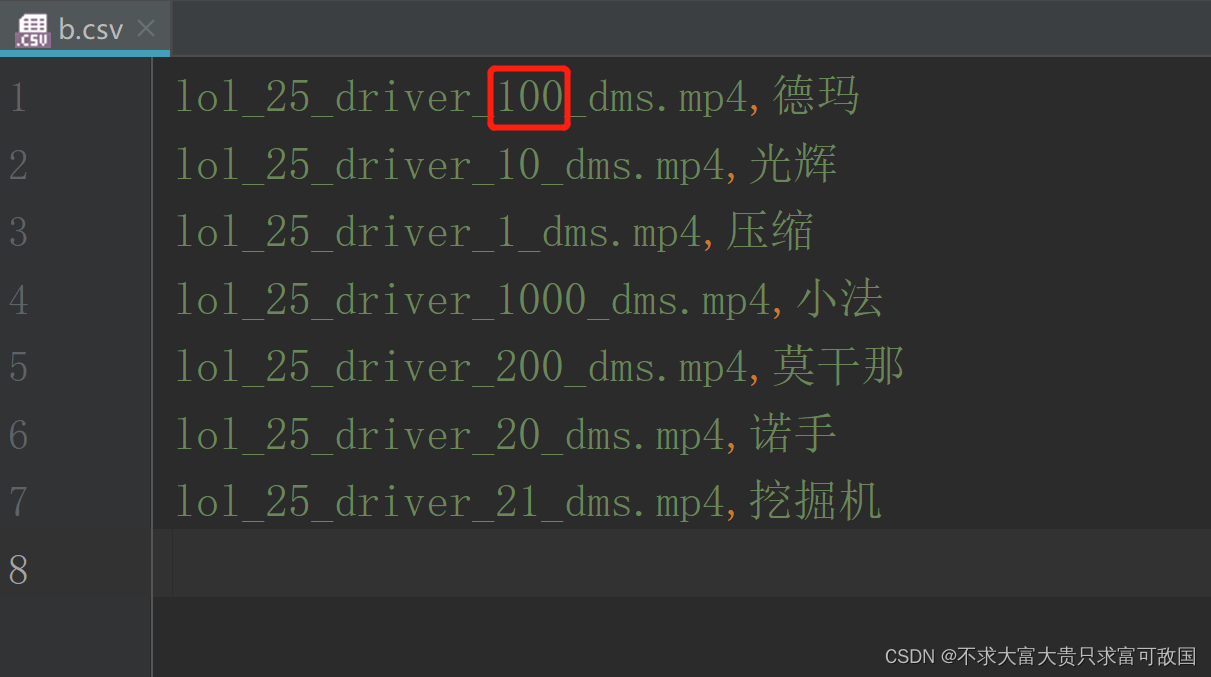
- Sort according to a number in a string in a column of CSV file
- @Jsonbackreference and @jsonmanagedreference (solve infinite recursion caused by bidirectional references in objects)
- [cloud native topic -45]:kubesphere cloud Governance - Introduction and overall architecture of enterprise container platform based on kubernetes
- ROS编译 调用第三方动态库(xxx.so)
- Indentation of tabs and spaces when writing programs for sublime text
- PLT in Matplotlib tight_ layout()
- The harm of game unpacking and the importance of resource encryption
- 2022.02.13 - 238. Maximum number of "balloons"
- Unsupported operation exception
猜你喜欢
随机推荐
Purpose of computer F1-F12
China Light conveyor belt in-depth research and investment strategy report (2022 Edition)
2022.02.13 - NC004. Print number of loops
sublime text中conda环境中plt.show无法弹出显示图片的问题
Navicat premium create MySQL create stored procedure
torch建立的网络模型使用torchviz显示
目标检测——Pytorch 利用mobilenet系列(v1,v2,v3)搭建yolov4目标检测平台
Function coritization
【嵌入式】Cortex M4F DSP库
How to effectively conduct automated testing?
TCP/IP协议
自动化测试框架有什么作用?上海专业第三方软件测试公司安利
ROS compilation calls the third-party dynamic library (xxx.so)
PC easy to use essential software (used)
Shift Operators
2022.02.13 - 238. Maximum number of "balloons"
egg. JS project deployment online server
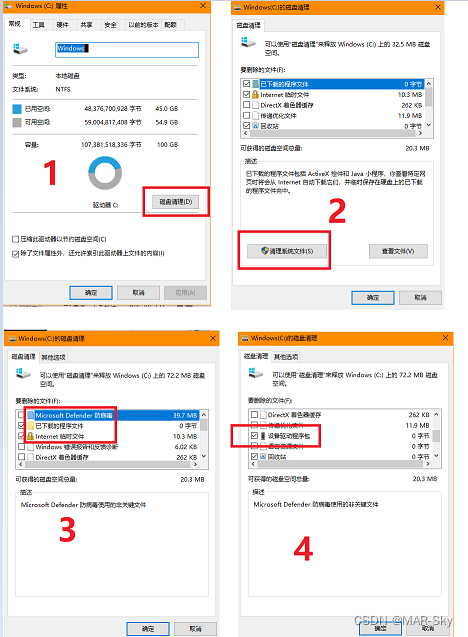
电脑清理,删除的系统文件
Roguelike游戏成破解重灾区,如何破局?
gcc动态库fPIC和fpic编译选项差异介绍