当前位置：网站首页>强化学习-学习笔记8 | Q-learning

强化学习-学习笔记8 | Q-learning

2022-07-07 16:26:00 【climerecho】

上一篇笔记认识了Sarsa，可以用来训练动作价值函数$Q_\pi$；本篇来学习Q-Learning，这是另一种 TD 算法，用来学习最优动作价值函数 Q-star，这就是之前价值学习中用来训练 DQN 的算法。

8. Q-learning

承接上一篇的疑惑，对比一下两个算法。

8.1 Sarsa VS Q-Learning

这两个都是 TD 算法，但是解决的问题不同。

Sarsa

Sarsa 训练动作价值函数 $Q_\pi(s,a)$；
TD target：$y_t = r_t + \gamma \cdot {Q_\pi(s_{t+1},a_{t+1})}$
价值网络是 $Q_\pi$ 的函数近似，Actor-Critic 方法中，用 Sarsa 更新价值网络(Critic)

Q-Learning

Q-learning 是训练最优动作价值函数 $Q^*(s,a)$
TD target :$y_t = r_t + \gamma \cdot {\mathop{max}\limits_{a}Q^*(s_{t+1},a_{t+1})}$，对 Q 求最大化
注意这里就是区别。
用Q-learning 训练DQN

个人总结区别在于Sarsa动作是随机采样的，而Q-learning是取期望最大值

下面推导 Q-Learning 算法。

8.2 Derive TD target

注意Q-learning 和 Sarsa 的 TD target 有区别。

之前 Sarsa 证明了这个等式：$Q_\pi({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot Q_\pi({S_{t+1}},{A_{t+1}})]$

等式的意思是，$Q_\pi$ 可以写成奖励以及 $Q_\pi$ 对下一时刻做出的估计；
等式两端都有 Q，并且对于所有的 $\pi$ 都成立。

所以把最优策略记作 $\pi^*$，上述公式对其也成立，有：

$Q_{\pi^*}({s_t},{a_t}) = \mathbb{E}[{R_t} + \gamma \cdot Q_{\pi^*}({S_{t+1}},{A_{t+1}})]$

通常把$Q_{\pi^*}$ 记作 $Q^*$，都可以表示最优动作价值函数，于是便得到：

$Q^*({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot Q^*({S_{t+1}},{A_{t+1}})]$

处理右侧期望中的 $Q^*$，将其写成最大化形式：

因为$A_{t+1} = \mathop{argmax}\limits_{a} Q^*({S_{t+1}},{a})$ ，A一定是最大化 $Q^*$的那个动作
解释：
给定状态$S_{t+1}$，Q* 会给所有动作打分，agent 会执行分值最高的动作。
因此 $Q^*({S_{t+1}},{A_{t+1}}) = \mathop{max}\limits_{a} Q^*({S_{t+1}},{a})$，$A_{t+1}$ 是最优动作，可以最大化 $Q^*$；
带入期望得到：$Q^({s_t},{a_t})=\mathbb{E}[{R_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({S_{t+1}},{a})]$
左边是 t 时刻的预测，等于右边的期望，期望中有最大化；期望不好求，用蒙特卡洛近似。用 $r_t \ s_{t+1}$ 代替 $R_t \ S_{t+1}$；
做蒙特卡洛近似：$\approx {r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a})$称为TD target $y_t$。
此处 $y_t$ 有一部分真实的观测，所以比左侧 Q-star 完全的猜测要靠谱，所以尽量要让左侧 Q-star 接近 $y_t$。

8.3 算法过程

a. 表格形式

观测一个transition$({s_t},{a_t},{r_t},{s_{t+1}})$
用 $s_{t+1} \ r_t$ 计算 TD target：${r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a})$
Q-star 就是下图这样的表格：

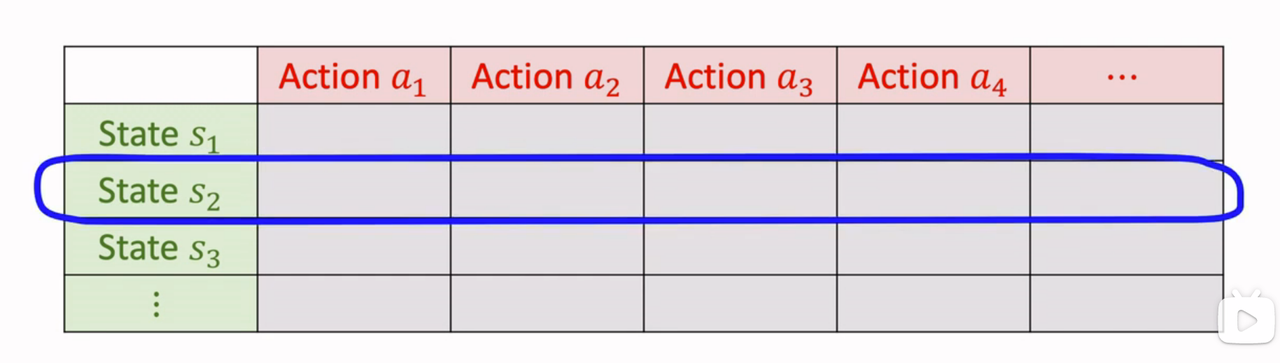
找到状态 $s_{t+1}$ 对应的行，找出最大元素，就是 $Q^*$ 关于 a 的最大值。

计算 TD error: $\delta_t = Q^*({s_t},{a_t}) - y_t$
更新$Q^*({s_t},{a_t}) \leftarrow Q^*({s_t},{a_t}) - \alpha \cdot \delta_t$，更新$(s_{t},a_t)$位置，让Q-star 值更接近 $y_t$

b. DQN形式

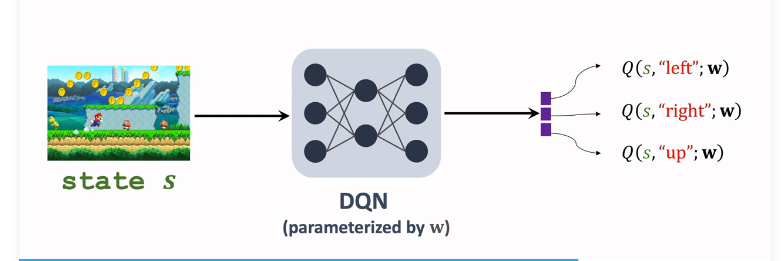
DQN $Q^*({s},{a};w)$近似 $Q^*({s},{a}) $，输入是当前状态 s，输出是对所有动作的打分；

接下来选择最大化价值的动作 ${a_t}= \mathop{argmax}\limits_{{a}} Q^*({S_{t+1}},{a},w)$，让 agent 执行 $a_t$；用收集到的 transitions 学习训练参数 w，让DQN 的打分 q 更准确；

用 Q-learning 训练DQN的过程：
观测一个transition $({s_t},{a_t},{r_t},{s_{t+1}})$
TD target: ${r_t} + \gamma \cdot \mathop{max}\limits_{a} Q^*({s_{t+1}},{a};w)$
TD error: $\delta_t = Q^*({s_t},{a_t};w) - y_t$
梯度下降，更新参数: $w \leftarrow w -\alpha \cdot \delta_t \cdot \frac{{s_t},{a_t};w}{\partial w}$