当前位置:网站首页>磁盘存储链式的B树与B+树
磁盘存储链式的B树与B+树
2022-07-07 16:03:00 【cheems~】
磁盘存储链式的B树与B+树
前言
本文介绍b树与b+树。并对b树的插入与删除做详细介绍,文末附代码。
本专栏知识点是通过零声教育的线上课学习,进行梳理总结写下文章,对c/c++linux课程感兴趣的读者,可以点击链接 C/C++后台高级服务器课程介绍 详细查看课程的服务。
磁盘结构分析与数据存储原理
我们知道常见的数据结构有链表,树,图等等,而树又可以分为二叉树,多叉树等等。对于链表来说,它可以找下一个结点在哪,而树不但可以找下一个数据结点在哪,树可以找两个,找三个,找多个(几叉),一个结点有几叉就可以找几个结点,通过一个结点可以找n个结点,这就是一个树形结构。
那么为什么要有多叉树呢?在学术上,通常解释为:树是为了降层高。那为什么要降层高呢?
对于多叉树来说,一个结点内,可能有多个key,所以多叉树是不能提高查询效率的(与二叉树相比)。但是它有一个好处,“一个结点内,可能有多个key”,这也就意味着多叉树的结点数量比较少,既然结点数量少,那么查找结点的次数就少。
注意,多叉树的作用:降低层高,使得结点数量变少,那么查找结点的次数就变少了。
我们知道cpu能直接存取内存,而不能直接存取磁盘。计算机给磁盘发送一个存取指令,磁盘通过旋转找到对应的盘面磁道扇区再读出来放入内存。磁盘为什么慢,就是因为磁盘寻址速度慢。每寻址一次,磁盘就要转一次。内存一次存取大约是10ns,磁盘一次存取是100ms。对于在内存中来说,多叉树的作用不大,但是对于磁盘来说,如果一个结点存了10个key,就可以少寻址很多次。所以多叉树的作用就是使得层高降低为了减少寻址次数。这也就是为什么磁盘的存储适合用b树或b+树的原因。
多叉树 -> 降低层高 -> 减少结点数量 -> 减少磁盘IO -> 提升性能
B树的定义
一颗M阶B树T,满足以下条件
- 每个结点至多拥有M课子树
- 根结点至少拥有两颗子树
- 除了根结点以外,其余每个分支结点至少拥有M/2课子树
- 所有的叶结点都在同一层上
- 有k棵子树的分支结点则存在k-1个关键字,关键字按照递增顺序进行排序
- 关键字数量满足 ceil( M/2 ) - 1 <= n <= M-1
B树与B+树的区别
在实际磁盘存储中往往选用的都是b+树
b+树相较于b树的优点:
- 关键字不保存数据,只用来索引,所有数据都保存在叶子结点(b树是每个关键字都保存数据)
- b+树的叶子结点是带有指针的,且叶结点本身按关键字从小到大顺序连接(适用于范围查询)
- b+树的中间结点不保存数据,所以磁盘页能容纳更多结点元素,更“矮胖”
B树插入的两种分裂
b树在插入的过程中,都会自上而下的检查当前节点是否可以分裂,如果关键字满了(k=M-1)则先分裂,再插入。并且插入都会插入到叶子结点中。b树插入会有两种分裂,一种是根结点分裂,一种是非根结点分裂。
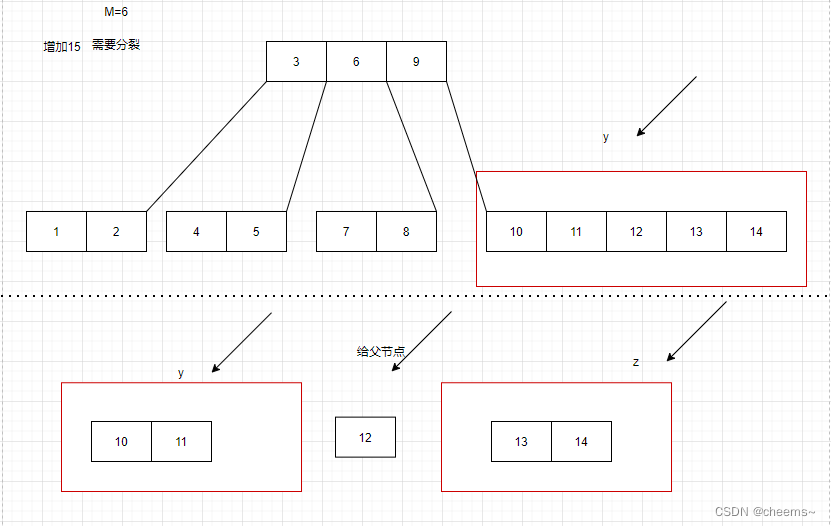
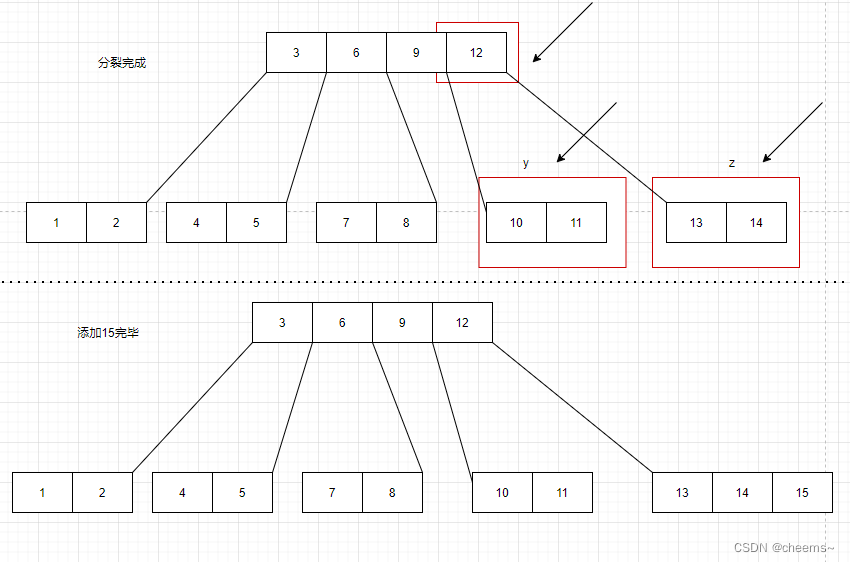
非根结点分裂
非根结点分裂过程:
1. 创建一个新结点,设为Z,原来的结点设为Y
2. 将Y的后半部分的关键字和子树赋给Z
3. 将Y中间那个关键字key给父结点
4. 父节点x增加一个关键字key和子树Z
根结点分裂
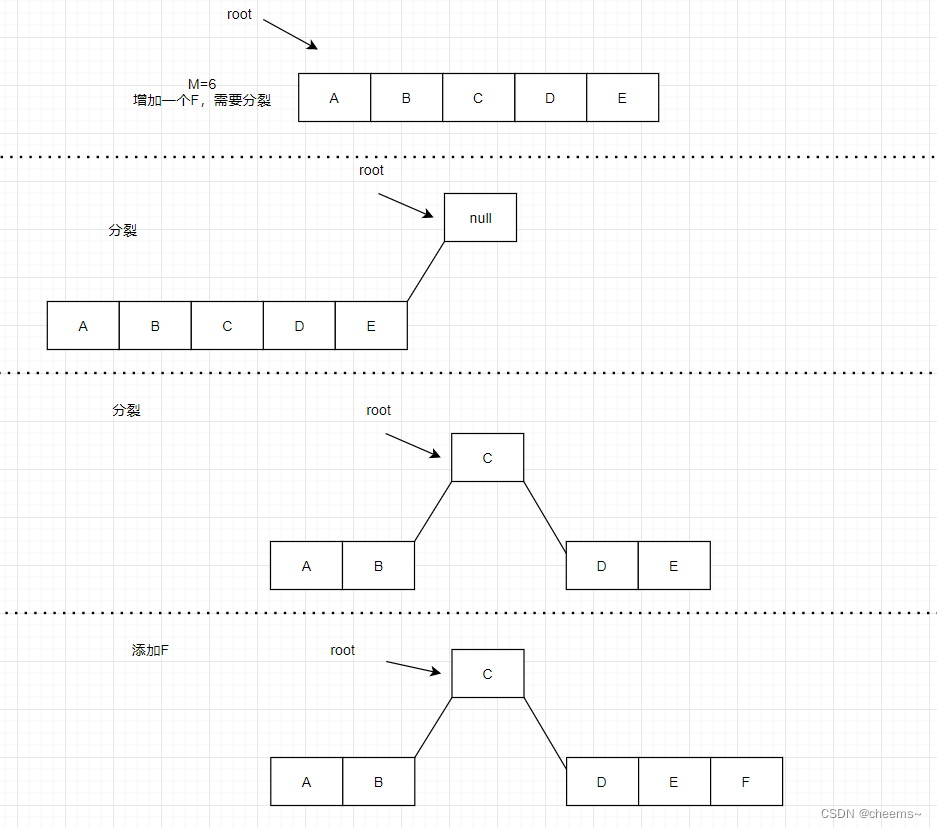
根结点分裂过程:
1. 创建一个新结点,设为node
2. 将b树的root指向node
3. node的第一个子树指向之前的根结点
4. 现在,根结点分裂就转化为了非根结点分裂
5. 执行非根结点分裂过程
插入分裂代码
//分裂
void btree_split_clild(struct btree *T, struct btree_node *x, int i) {
//y 需要分裂的结点
struct btree_node *y = x->children[i];
//新节点
struct btree_node *z = btree_create_node(T->t, y->leaf);
int j = 0;
z->num = T->t - 1;
//把y后半部分的key和子树copy到z里
for (j = 0; j < T->t - 1; j++) {
z->keys[j] = y->keys[j + T->t];
}
if (y->leaf == 0) {
for (j = 0; j < T->t; j++) {
z->children[j] = y->children[j + T->t];
}
}
//y结点修改数量
y->num = T->t - 1;
//将父节点x增加一个key和子树z
for (j = x->num; j >= i + 1; j--) {
x->children[j + 1] = x->children[j];
}
x->children[i + 1] = z;
for (j = x->num - 1; j >= i; j--) {
x->keys[j + 1] = x->keys[j];
}
x->keys[i] = y->keys[T->t - 1];
x->num++;
}
void btree_insert_nonfull(struct btree *T, struct btree_node *x, KEY_TYPE key) {
int i = x->num - 1;
if (x->leaf) {
while (i >= 0 && x->keys[i] > key) {
x->keys[i + 1] = x->keys[i];
i--;
}
x->keys[i + 1] = key;
x->num++;
}
else {
while (i >= 0 && x->keys[i] > key)i--;
if (x->children[i + 1]->num == 2 * T->t - 1) {
btree_split_clild(T, x, i + 1);
if (key > x->keys[i + 1])i++;
}
btree_insert_nonfull(T, x->children[i + 1], key);
}
}
void btree_insert(struct btree *T, KEY_TYPE key) {
struct btree_node *root = T->root;
//如果根结点满了,根节点分裂再插入
if (root->num == 2 * T->t - 1) {
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->children[0] = root;
btree_split_clild(T, node, 0);
int i = 0;
if (key > node->keys[0]) i++;
btree_insert_nonfull(T, node->children[i], key);
}
else {
btree_insert_nonfull(T, root, key);
}
}
B树删除的前后借位与节点合并
为什么删除关键字要借位或者合并呢?因为我们需要满足b树的定义
判断子树关键字的数量
- 相邻两棵子树都是M/2-1 ,则合并
- 左子树大于M/2-1,向左借位
- 右子树大于M/2-1,向右借位
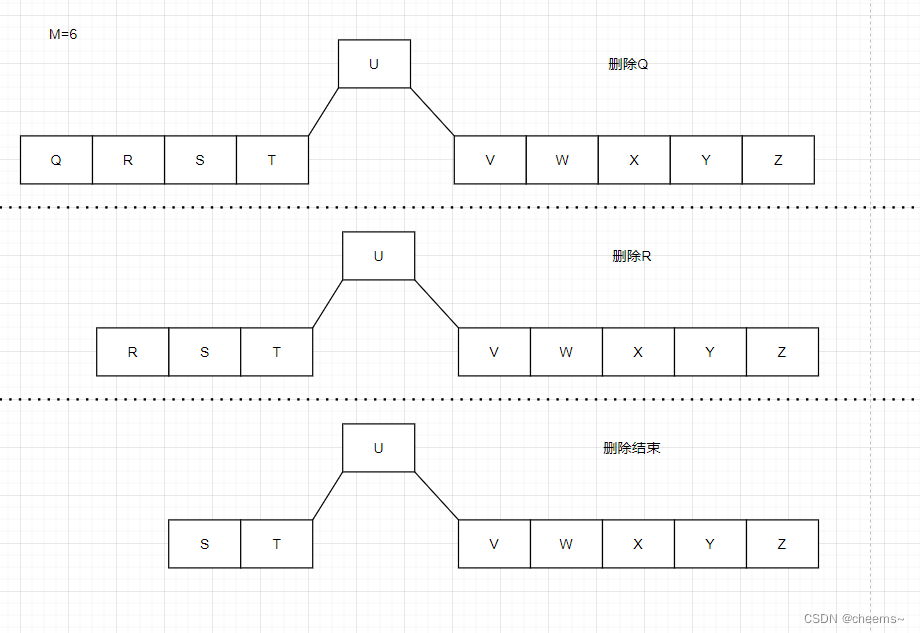
关键字在叶子结点中,直接删除
关键字在叶子结点中
- 直接删除
当前结点为内结点,且左孩子至少包含M/2个关键字,则向前借位再删除
当前结点为内结点,且左孩子至少包含M/2个关键字
- 先借位
- 在删除
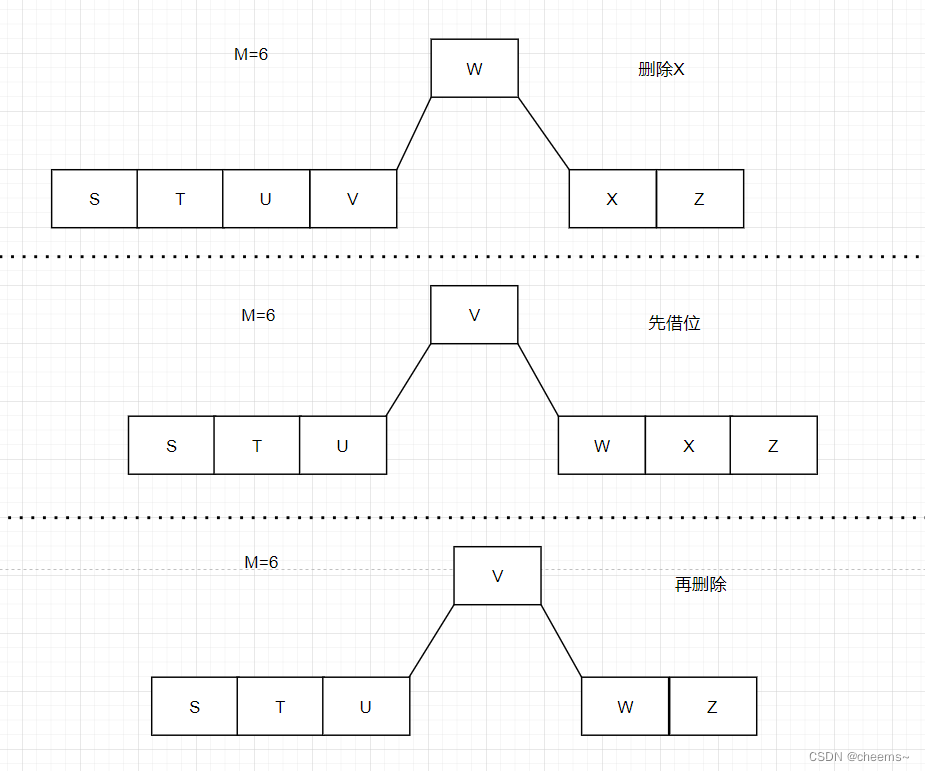
当前结点为内结点,且右孩子至少包含M/2个关键字,则向后借位再删除
当前结点为内结点,且右孩子至少包含M/2个关键字
- 先借位
- 在删除
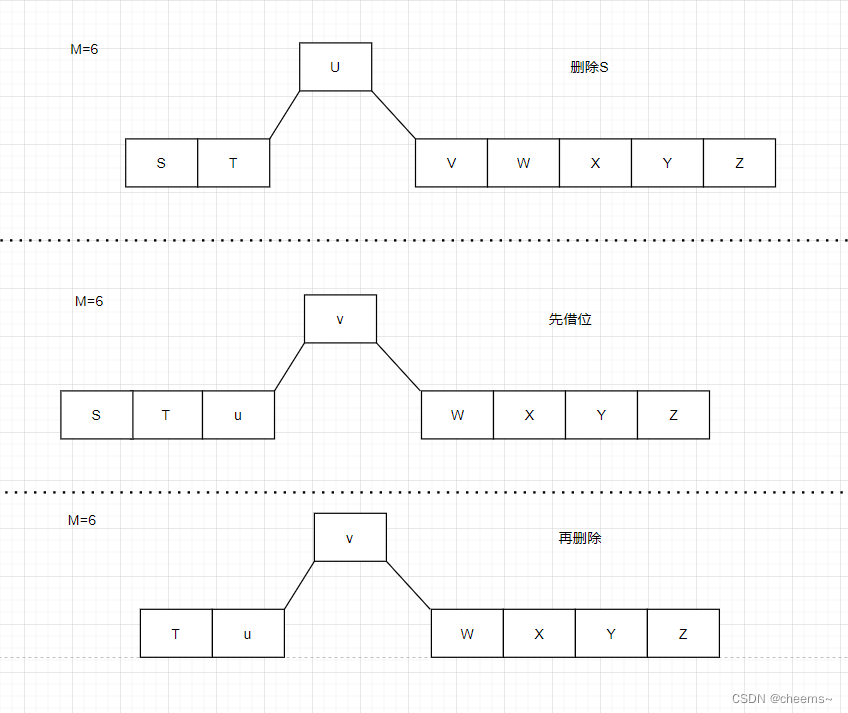
左右孩子都是M/2-1个关键字,则合并再删除
左右孩子都是M/2-1个关键
- 先合并
- 再删除
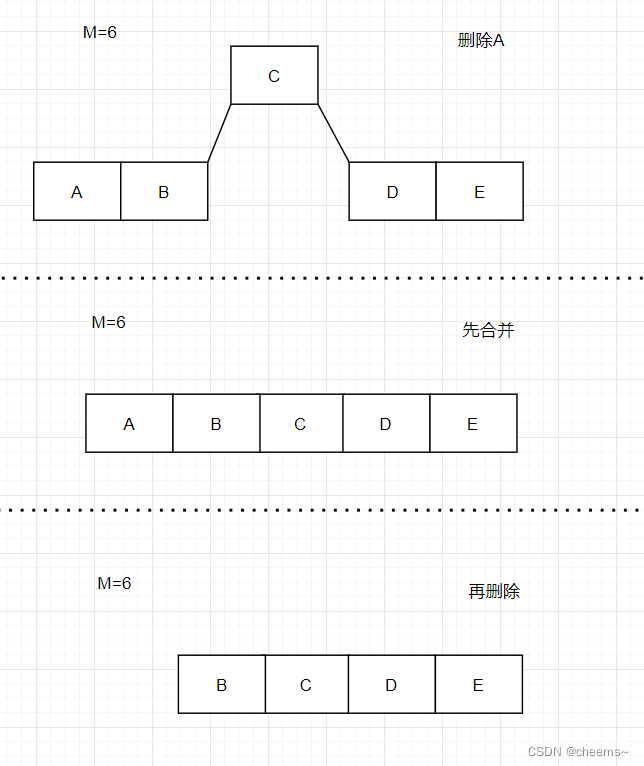
删除合并代码
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
//左右子树
btree_node *left = node->children[idx];
btree_node *right = node->children[idx + 1];
int i = 0;
//data merge
left->keys[T->t - 1] = node->keys[idx];
for (i = 0; i < T->t - 1; i++) {
left->keys[T->t + i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0; i < T->t; i++) {
left->children[T->t + i] = right->children[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx + 1; i < node->num; i++) {
node->keys[i - 1] = node->keys[i];
node->children[i] = node->children[i + 1];
}
node->children[i + 1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
void btree_delete_key(btree *T, btree_node *node, KEY_TYPE key) {
//如果删除的是null直接返回
if (node == NULL) return;
int idx = 0, i;
//找到key的位置
while (idx < node->num && key > node->keys[idx]) {
idx++;
}
//如果key是内节点
if (idx < node->num && key == node->keys[idx]) {
//如果内节点是叶子节点,直接删
if (node->leaf) {
for (i = idx; i < node->num - 1; i++) {
node->keys[i] = node->keys[i + 1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) {
//如果整个树都被删了
free(node);
T->root = NULL;
}
return;
}
//前面的结点借位
else if (node->children[idx]->num >= T->t) {
btree_node *left = node->children[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
}
//后面的结点借位
else if (node->children[idx + 1]->num >= T->t) {
btree_node *right = node->children[idx + 1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
}
else {
//合并
btree_merge(T, node, idx);//合并了一个子树上
btree_delete_key(T, node->children[idx], key);
}
}
else {
//key不在这层,进入下层
btree_node *child = node->children[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return;
}
//说明需要借位
if (child->num == T->t - 1) {
//left child right三个节点
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->children[idx - 1];
if (idx + 1 <= node->num)
right = node->children[idx + 1];
//说明有一个可以借位
if ((left && left->num >= T->t) || (right && right->num >= T->t)) {
int richR = 0;
if (right) {
richR = 1;
}
//如果右子树比左子树的key多,则richR=1
if (left && right) {
richR = (right->num > left->num) ? 1 : 0;
}
//从下一个借
if (right && right->num >= T->t && richR) {
child->keys[child->num] = node->keys[idx];//将父节点的key拿来,拿子树,右节点的第一个子树
child->children[child->num + 1] = right->children[0];
child->num++;
//父节点借右节点的第一个key
node->keys[idx] = right->keys[0];
//右节点被借位,删除一些东西
for (i = 0; i < right->num - 1; i++) {
right->keys[i] = right->keys[i + 1];
right->children[i] = right->children[i + 1];
}
right->keys[right->num - 1] = 0;
right->children[right->num - 1] = right->children[right->num];
right->children[right->num] = NULL;
right->num--;
}
//从上一个借
else {
for (i = child->num; i > 0; i--) {
child->keys[i] = child->keys[i - 1];
child->children[i + 1] = child->children[i];
}
child->children[1] = child->children[0];
//将左子树的最后一个子树拿来
child->children[0] = left->children[left->num];
//拿父节点的key
child->keys[0] = node->keys[idx - 1];
child->num++;
//父节点那左子树的key
node->keys[idx - 1] = left->keys[left->num - 1];
left->keys[left->num - 1] = 0;
left->children[left->num] = NULL;
left->num--;
}
}
//合并
else if ((!left || (left->num == T->t - 1)) && (!right || (right->num == T->t - 1))) {
//把node和left合并
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx - 1);
child = left;
}
//把node和right合并
else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
//递归下一层
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_TYPE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
B树插入,删除,遍历,查找代码
#include <stdio.h>
#include <stdlib.h>
//b tree
#define M 3//最好是偶数,易于分裂。阶
typedef int KEY_TYPE;
//btree节点
struct btree_node {
struct btree_node **children;//子树
KEY_TYPE *keys;//关键字
int num;//关键字数量
int leaf;//是否是叶子结点 1yes,0no
};
//btree
struct btree {
struct btree_node *root;
int t;
};
//创建一个结点
struct btree_node *btree_create_node(int t, int leaf) {
struct btree_node *node = (struct btree_node *) calloc(1, sizeof(struct btree_node));
if (node == NULL)return NULL;
node->num = 0;
node->keys = (KEY_TYPE *) calloc(1, (2 * t - 1) * sizeof(KEY_TYPE));
node->children = (struct btree_node **) calloc(1, (2 * t) * sizeof(struct btree_node *));
node->leaf = leaf;
return node;
}
//销毁一个结点
struct btree_node *btree_destroy_node(struct btree_node *node) {
if (node) {
if (node->keys) {
free(node->keys);
}
if (node->children) {
free(node->children);
}
free(node);
}
}
//创建一个btree
void btree_create(btree *T, int t) {
T->t = t;
struct btree_node *x = btree_create_node(t, 1);
T->root = x;
}
//分裂
void btree_split_clild(struct btree *T, struct btree_node *x, int i) {
//y 需要分裂的结点
struct btree_node *y = x->children[i];
//新节点
struct btree_node *z = btree_create_node(T->t, y->leaf);
int j = 0;
z->num = T->t - 1;
//把y后半部分的key和子树copy到z里
for (j = 0; j < T->t - 1; j++) {
z->keys[j] = y->keys[j + T->t];
}
if (y->leaf == 0) {
for (j = 0; j < T->t; j++) {
z->children[j] = y->children[j + T->t];
}
}
//y结点修改数量
y->num = T->t - 1;
//将父节点x增加一个key和子树z
for (j = x->num; j >= i + 1; j--) {
x->children[j + 1] = x->children[j];
}
x->children[i + 1] = z;
for (j = x->num - 1; j >= i; j--) {
x->keys[j + 1] = x->keys[j];
}
x->keys[i] = y->keys[T->t - 1];
x->num++;
}
void btree_insert_nonfull(struct btree *T, struct btree_node *x, KEY_TYPE key) {
int i = x->num - 1;
if (x->leaf) {
while (i >= 0 && x->keys[i] > key) {
x->keys[i + 1] = x->keys[i];
i--;
}
x->keys[i + 1] = key;
x->num++;
}
else {
while (i >= 0 && x->keys[i] > key)i--;
if (x->children[i + 1]->num == 2 * T->t - 1) {
btree_split_clild(T, x, i + 1);
if (key > x->keys[i + 1])i++;
}
btree_insert_nonfull(T, x->children[i + 1], key);
}
}
void btree_insert(struct btree *T, KEY_TYPE key) {
struct btree_node *root = T->root;
//如果根结点满了,根节点分裂
if (root->num == 2 * T->t - 1) {
btree_node *node = btree_create_node(T->t, 0);
T->root = node;
node->children[0] = root;
btree_split_clild(T, node, 0);
int i = 0;
if (key > node->keys[0]) i++;
btree_insert_nonfull(T, node->children[i], key);
}
else {
btree_insert_nonfull(T, root, key);
}
}
//{child[idx], key[idx], child[idx+1]}
void btree_merge(btree *T, btree_node *node, int idx) {
//左右子树
btree_node *left = node->children[idx];
btree_node *right = node->children[idx + 1];
int i = 0;
//data merge
left->keys[T->t - 1] = node->keys[idx];
for (i = 0; i < T->t - 1; i++) {
left->keys[T->t + i] = right->keys[i];
}
if (!left->leaf) {
for (i = 0; i < T->t; i++) {
left->children[T->t + i] = right->children[i];
}
}
left->num += T->t;
//destroy right
btree_destroy_node(right);
//node
for (i = idx + 1; i < node->num; i++) {
node->keys[i - 1] = node->keys[i];
node->children[i] = node->children[i + 1];
}
node->children[i + 1] = NULL;
node->num -= 1;
if (node->num == 0) {
T->root = left;
btree_destroy_node(node);
}
}
void btree_delete_key(btree *T, btree_node *node, KEY_TYPE key) {
//如果删除的是null直接返回
if (node == NULL) return;
int idx = 0, i;
//找到key的位置
while (idx < node->num && key > node->keys[idx]) {
idx++;
}
//如果key是内节点
if (idx < node->num && key == node->keys[idx]) {
//如果内节点是叶子节点,直接删
if (node->leaf) {
for (i = idx; i < node->num - 1; i++) {
node->keys[i] = node->keys[i + 1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) {
//如果整个树都被删了
free(node);
T->root = NULL;
}
return;
}
//前面的结点借位
else if (node->children[idx]->num >= T->t) {
btree_node *left = node->children[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
}
//后面的结点借位
else if (node->children[idx + 1]->num >= T->t) {
btree_node *right = node->children[idx + 1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
}
else {
//合并
btree_merge(T, node, idx);//合并了一个子树上
btree_delete_key(T, node->children[idx], key);
}
}
else {
//key不在这层,进入下层
btree_node *child = node->children[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return;
}
//说明需要借位
if (child->num == T->t - 1) {
//left child right三个节点
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->children[idx - 1];
if (idx + 1 <= node->num)
right = node->children[idx + 1];
//说明有一个可以借位
if ((left && left->num >= T->t) || (right && right->num >= T->t)) {
int richR = 0;
if (right) {
richR = 1;
}
//如果右子树比左子树的key多,则richR=1
if (left && right) {
richR = (right->num > left->num) ? 1 : 0;
}
//从下一个借
if (right && right->num >= T->t && richR) {
child->keys[child->num] = node->keys[idx];//将父节点的key拿来,拿子树,右节点的第一个子树
child->children[child->num + 1] = right->children[0];
child->num++;
//父节点借右节点的第一个key
node->keys[idx] = right->keys[0];
//右节点被借位,删除一些东西
for (i = 0; i < right->num - 1; i++) {
right->keys[i] = right->keys[i + 1];
right->children[i] = right->children[i + 1];
}
right->keys[right->num - 1] = 0;
right->children[right->num - 1] = right->children[right->num];
right->children[right->num] = NULL;
right->num--;
}
//从上一个借
else {
for (i = child->num; i > 0; i--) {
child->keys[i] = child->keys[i - 1];
child->children[i + 1] = child->children[i];
}
child->children[1] = child->children[0];
//将左子树的最后一个子树拿来
child->children[0] = left->children[left->num];
//拿父节点的key
child->keys[0] = node->keys[idx - 1];
child->num++;
//父节点那左子树的key
node->keys[idx - 1] = left->keys[left->num - 1];
left->keys[left->num - 1] = 0;
left->children[left->num] = NULL;
left->num--;
}
}
//合并
else if ((!left || (left->num == T->t - 1)) && (!right || (right->num == T->t - 1))) {
//把node和left合并
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx - 1);
child = left;
}
//把node和right合并
else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
//递归下一层
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_TYPE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
void btree_traverse(btree_node *x) {
int i = 0;
for (i = 0; i < x->num; i++) {
if (x->leaf == 0)
btree_traverse(x->children[i]);
printf("%C ", x->keys[i]);
}
if (x->leaf == 0) btree_traverse(x->children[i]);
}
void btree_print(btree *T, btree_node *node, int layer) {
btree_node *p = node;
int i;
if (p) {
printf("\nlayer = %d keynum = %d is_leaf = %d\n", layer, p->num, p->leaf);
for (i = 0; i < node->num; i++)
printf("%c ", p->keys[i]);
printf("\n");
#if 0
printf("%p\n", p);
for(i = 0; i <= 2 * T->t; i++)
printf("%p ", p->childrens[i]);
printf("\n");
#endif
layer++;
for (i = 0; i <= p->num; i++)
if (p->children[i])
btree_print(T, p->children[i], layer);
}
else printf("the tree is empty\n");
}
int btree_bin_search(btree_node *node, int low, int high, KEY_TYPE key) {
int mid;
if (low > high || low < 0 || high < 0) {
return -1;
}
while (low <= high) {
mid = (low + high) / 2;
if (key > node->keys[mid]) {
low = mid + 1;
}
else {
high = mid - 1;
}
}
return low;
}
int main() {
btree T = {
0};
btree_create(&T, 3);
srand(48);
int i = 0;
char key[27] = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
for (i = 0; i < 26; i++) {
//key[i] = rand() % 1000;
printf("%c ", key[i]);
btree_insert(&T, key[i]);
}
btree_print(&T, T.root, 0);
for (i = 0; i < 26; i++) {
printf("\n---------------------------------\n");
btree_delete(&T, key[25 - i]);
//btree_traverse(T.root);
btree_print(&T, T.root, 0);
}
}
边栏推荐
- Alertdialog create dialog
- Deep learning - make your own dataset
- Cf:c. factors and powers of two [DP + sort + Select Board + select several numbers equal to the minimum number of known sums]
- What skills can you master to be a "master tester" when doing software testing?
- Automated testing: a practical skill that everyone wants to know about robot framework
- yolo训练过程中批量导入requirments.txt中所需要的包
- [distributed theory] (I) distributed transactions
- Self made dataset in pytoch for dataset rewriting
- 现在网上期货开户安全吗?国内有多少家正规的期货公司?
- Pro2: modify the color of div block
猜你喜欢

Using stored procedures, timers, triggers to solve data analysis problems

备份阿里云实例-oss-browser
<代码随想录二刷>链表
Taffydb open source JS database
2021-06-28
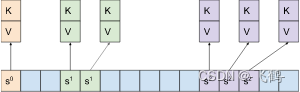
Tips of the week 136: unordered containers

More than 10000 units were offline within ten days of listing, and the strength of Auchan Z6 products was highly praised

2021年全国平均工资出炉,你达标了吗?
Supplementary instructions to relevant rules of online competition

回归测试的分类
随机推荐
yolo训练过程中批量导入requirments.txt中所需要的包
Pro2: modify the color of div block
[answer] if the app is in the foreground, the activity will not be recycled?
3分钟学会制作动态折线图!
深度学习-制作自己的数据集
Introduction to OTA technology of Internet of things
Alertdialog create dialog
Chapter 3 business function development (user login)
万字保姆级长文——Linkedin元数据管理平台Datahub离线安装指南
[re understand the communication model] the application of reactor mode in redis and Kafka
Use onedns to perfectly solve the optimization problem of office network
Chapter 3 business function development (safe exit)
mui侧边导航锚点定位js特效
【OKR目标管理】价值分析
Ten thousand words nanny level long article -- offline installation guide for datahub of LinkedIn metadata management platform
Hutool - 轻量级 DB 操作解决方案
【蓝桥杯集训100题】scratch从小到大排序 蓝桥杯scratch比赛专项预测编程题 集训模拟练习题第17题
2021-06-28
Simple loading animation
Tips of this week 135: test the contract instead of implementation