当前位置:网站首页>Quick completion guide for manipulator (IX): forward kinematics analysis
Quick completion guide for manipulator (IX): forward kinematics analysis
2022-07-05 15:44:00 【Lie on me】
Directory :
Quick completion guide of mechanical arm ( zero ): Main contents and analysis methods of the guide
Quick completion guide of mechanical arm ( One ): The development of manipulator
Quick completion guide of mechanical arm ( Two ): Application of mechanical arm
Quick completion guide of mechanical arm ( 3、 ... and ): Mechanical structure of mechanical arm
Quick completion guide of mechanical arm ( Four ): Reducer of key components of mechanical arm
Quick completion guide of mechanical arm ( 5、 ... and ): End actuators
Quick completion guide of mechanical arm ( 6、 ... and ): Stepper motor driver
Quick completion guide of mechanical arm ( 7、 ... and ): Description method of robot arm posture
Quick completion guide of mechanical arm ( 8、 ... and ): Kinematic modeling ( standard DH Law )
Quick completion guide of mechanical arm ( Nine ): Forward kinematics analysis
In chapter eight , We have got the of the manipulator used DH Parameters , As shown in the following table :
| Connecting rod number | Range of joint variables | ||||
| 1 | 64.2 | -90 | 169.77 | θ1 | (-170,+170) |
| 2 | 305 | 0 | 0 | θ2 | (-132,0) |
| 3 | 0 | 90 | 0 | θ3 | (1,141) |
| 4 | 0 | -90 | -222.63 | θ4 | (-165,+ 165) |
| 5 | 0 | 90 | 0 | θ5 | (-105,+105) |
| 6 | 0 | 0 | -36.25 | θ6 | (-155,+155) |
In determining the DH Parameters after , Use Homogeneous transformation matrix Describe the rotation between coordinate systems 、 Translation relationship , The forward kinematics equation of the manipulator is constructed by using the homogeneous transformation matrix , Based on this, the forward kinematics analysis of the six degree of freedom manipulator is carried out .
One 、 Construct the forward kinematics equation of the manipulator
From the coordinate system i To the coordinate system i-1 Homogeneous transformation matrix ![]() Is a joint variable only
Is a joint variable only ![]() Related functions , This article is written as
Related functions , This article is written as ![]() . The derivation is listed below
. The derivation is listed below ![]() The process of , In a coordinate system i And coordinate system i-1 For example , Coordinate transformation rotation of coordinate system 、 The translation process is shown in the following figure .
The process of , In a coordinate system i And coordinate system i-1 For example , Coordinate transformation rotation of coordinate system 、 The translation process is shown in the following figure .
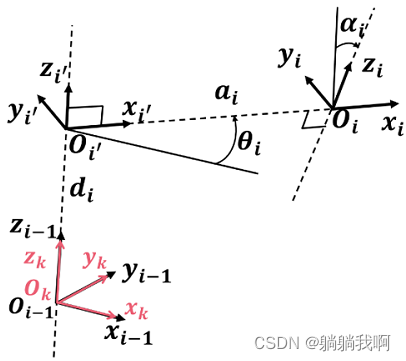
First , Set a coordinate system k And coordinate system i-1 Align , Then set the coordinate system k Along axis zi-1![]() translation di
translation di![]() And around the axis zi-1
And around the axis zi-1![]() rotate θi
rotate θi![]() . Now the coordinate system k Has been linked to the coordinate system
. Now the coordinate system k Has been linked to the coordinate system ![]() Align , The process can be described as
Align , The process can be described as
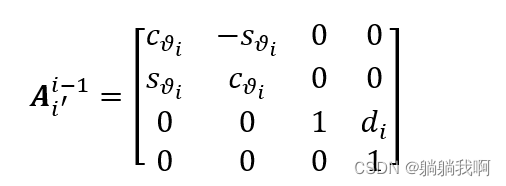
In style ![]() Express cos(n) ,
Express cos(n) ,![]() Express sin(n), It is necessary to consider the x Initial included angle between shafts θ.
Express sin(n), It is necessary to consider the x Initial included angle between shafts θ.
next , Set coordinate system k Along axis xi'![]() translation
translation ![]() And rotate around it
And rotate around it ![]() , This makes the coordinate system and Coordinate system i Align , The process can be described as
, This makes the coordinate system and Coordinate system i Align , The process can be described as
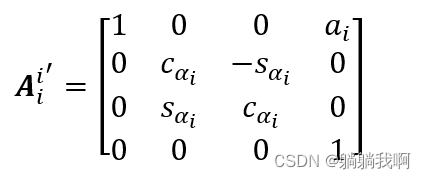
From the coordinate system i To the coordinate system i-1 The homogeneous transformation matrix of can be multiplied by a single transformation matrix ![]() And
And ![]() obtain , by
obtain , by
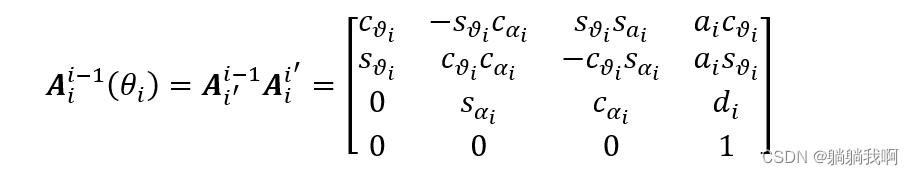
According to the above formula, a homogeneous transformation matrix representing the relative position and direction between coordinate systems can be obtained , Regard it as the homogeneous transformation matrix of each joint , The results are shown in the table below .
| Joint number | Homogeneous transformation matrix |
| 1 |  |
| 2 | 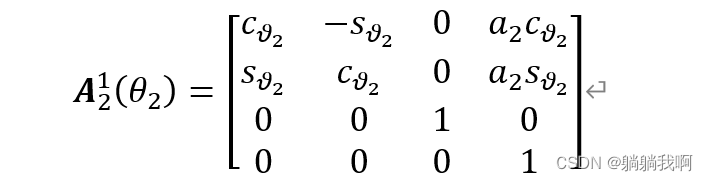 |
| 3 | 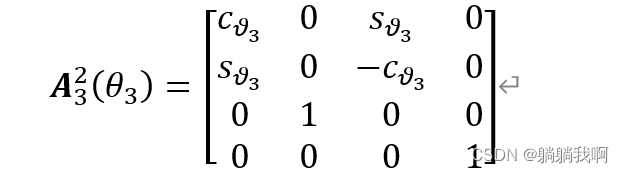 |
| 4 | 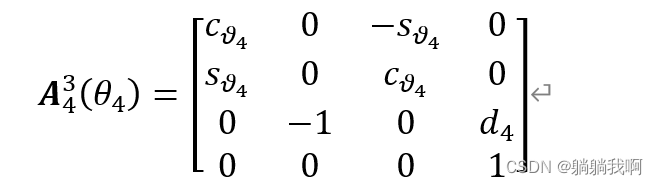 |
| 5 | 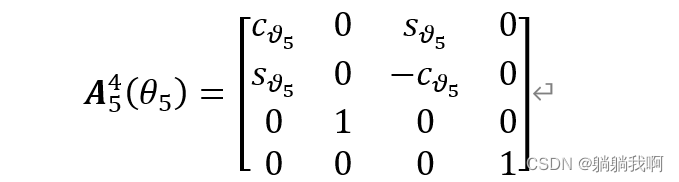 |
| 6 | 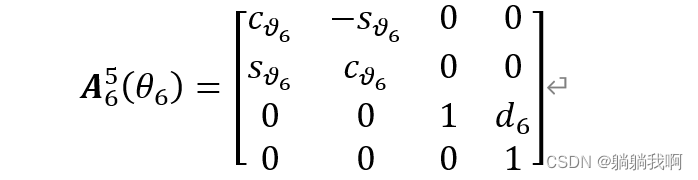 |
Because of the coordinate system 0 Coincide with the base coordinate system , And because of the coordinate system 6 That is to say Tool coordinate system , So there is
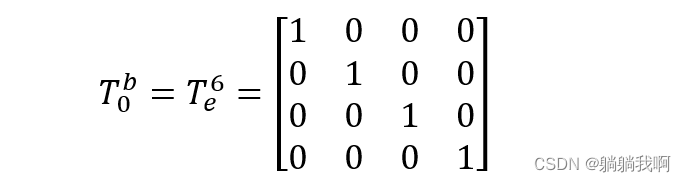
The forward kinematics equation used to represent the tool coordinate system relative to the base coordinate system can be obtained from the above table 6 A homogeneous transformation matrix is right multiplied to obtain , by
![]()
The first three joints make up Anthropomorphic arm , Then its forward kinematics equation is expressed as
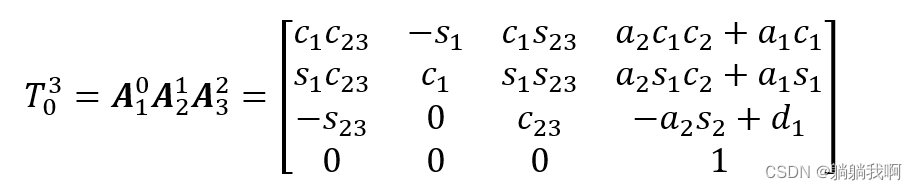
among ,![]() And
And ![]() respectively sin(qj+…+qk) and cos(qj+…+qk) .
respectively sin(qj+…+qk) and cos(qj+…+qk) .
The latter three joints form Spherical wrist , The same can be , The forward kinematics equation of spherical wrist can be expressed as
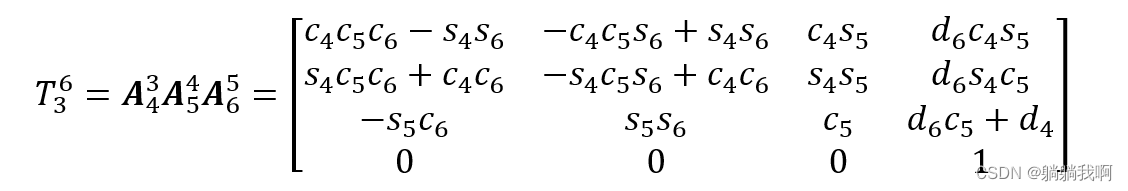
Then it can be concluded that the forward kinematics equation of the manipulator is :
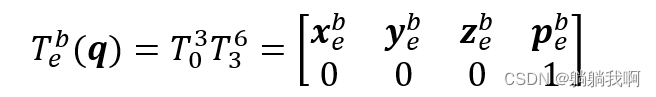
among ,![]() Is a vector composed of joint variables , vector q This space is called Joint space .
Is a vector composed of joint variables , vector q This space is called Joint space .
Calculated , The position of the end effector is expressed as
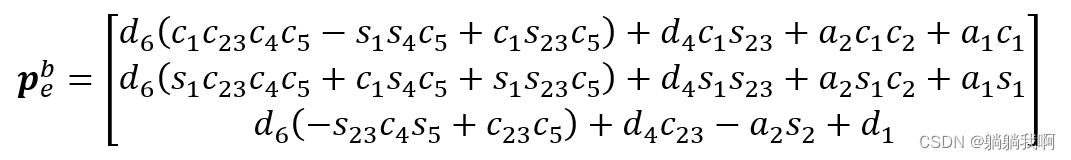
Empathy , The attitude of the end effector can be expressed as
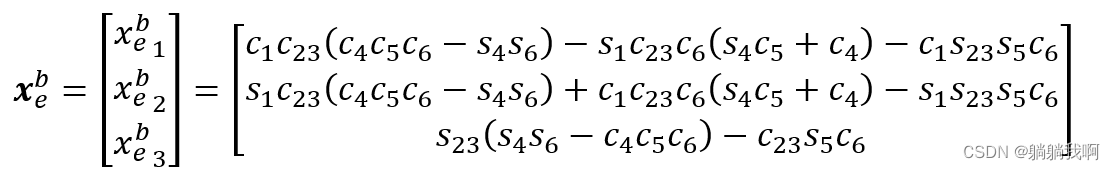
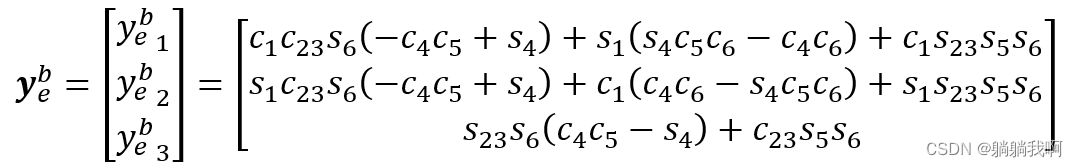
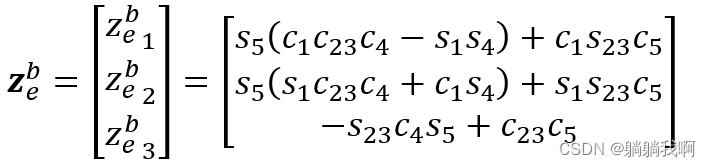
Final , End effector RPY horn It can be expressed as a transcendental function about joint variables , namely
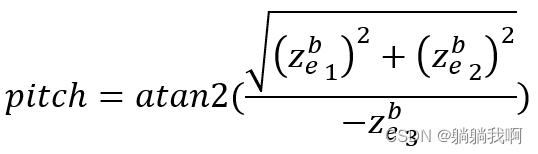


thus , The forward kinematics formula of the manipulator is solved , When we substitute joint variables into the formula, we can get the pose of the end effector .
Two 、 Programming realization of solving forward kinematics equation
Due to the large amount of computation of the forward kinematics equation , In order to improve the operation speed , We choose to use the upper computer to complete the calculation . Use Python Write the solution function of the positive motion equation of the manipulator CalcFwdKin(), Input parameter is 6 Joint variables , The output is the position and attitude of the end effector .
The forward kinematics equation of the manipulator is the transcendental function of the joint variables , There are a lot of trigonometric function calculation and matrix operation in the process of solving , So we introduce Python Self contained math Standard library , This module provides many mathematical operation functions for floating-point numbers .
![]()
In the process of solving the forward kinematics equation math.sin()、math.cos() And math.atan2() Complete the calculation of trigonometric function ; Use math.sqrt() Find the square root ; adopt math.degrees() And math.radians() Complete the conversion between radian and angle .
To use math Function must be imported first :
import math
The effect is shown below :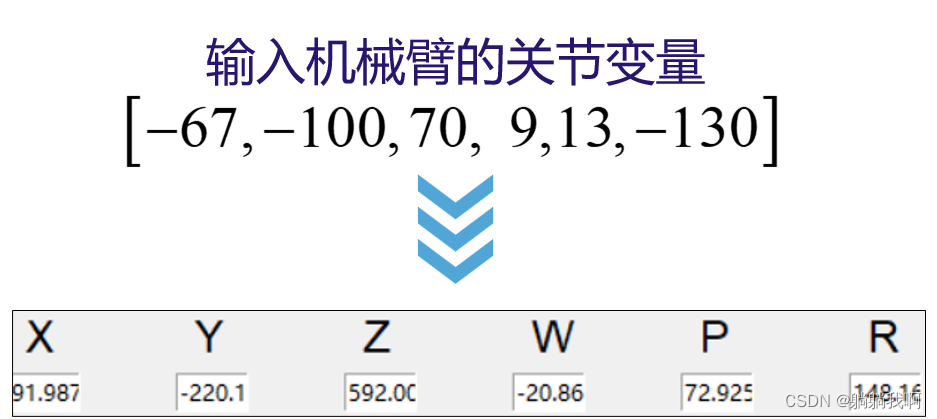
############## DH TABLE ################
############## DH Parameter table ###############
C13 = C4
C14 = C5
C15 = C6
C16 = C7
C17 = C8
C18 = C9
D13 = math.radians(DHr1)
D14 = math.radians(DHr2)
D15 = math.radians(DHr3)
D16 = math.radians(DHr4)
D17 = math.radians(DHr5)
D18 = math.radians(DHr6)
E13 = DHd1
E14 = DHd2
E15 = DHd3
E16 = DHd4
E17 = DHd5
E18 = DHd6
F13 = DHa1
F14 = DHa2
F15 = DHa3
F16 = DHa4
F17 = DHa5
F18 = DHa6
## WORK FRAME INPUT
H13 = float(UFxEntryField.get())
H14 = float(UFyEntryField.get())
H15 = float(UFzEntryField.get())
H16 = float(UFrxEntryField.get())
H17 = float(UFryEntryField.get())
H18 = float(UFrzEntryField.get())
## TOOL FRAME INPUT
J13 = float(TFxEntryField.get())
J14 = float(TFyEntryField.get())
J15 = float(TFzEntryField.get())
J16 = float(TFrxEntryField.get())
J17 = float(TFryEntryField.get())
J18 = float(TFrzEntryField.get())
## WORK FRAME TABLE
B21 = math.cos(math.radians(H18))*math.cos(math.radians(H17))
B22 = math.sin(math.radians(H18))*math.cos(math.radians(H17))
B23 = -math.sin(math.radians(H18))
B24 = 0
C21 = -math.sin(math.radians(H18))*math.cos(math.radians(H16))+math.cos(math.radians(H18))*math.sin(math.radians(H17))*math.sin(math.radians(H16))
C22 = math.cos(math.radians(H18))*math.cos(math.radians(H16))+math.sin(math.radians(H18))*math.sin(math.radians(H17))*math.sin(math.radians(H16))
C23 = math.cos(math.radians(H17))*math.sin(math.radians(H16))
C24 = 0
D21 = math.sin(math.radians(H18))*math.sin(math.radians(H16))+math.cos(math.radians(H18))*math.sin(math.radians(H17))*math.cos(math.radians(H16))
D22 = -math.cos(math.radians(H18))*math.sin(math.radians(H16))+math.sin(math.radians(H18))*math.sin(math.radians(H17))*math.cos(math.radians(H16))
D23 = math.cos(math.radians(H17))*math.cos(math.radians(H16))
D24 = 0
E21 = H13
E22 = H14
E23 = H15
E24 = 1
## J1 FRAME
B27 = math.cos(C13)
B28 = math.sin(C13)
B29 = 0
B30 = 0
C27 = -math.sin(C13)*math.cos(D13)
C28 = math.cos(C13)*math.cos(D13)
C29 = math.sin(D13)
C30 = 0
D27 = math.sin(C13)*math.sin(D13)
D28 = -math.cos(C13)*math.sin(D13)
D29 = math.cos(D13)
D30 = 0
E27 = F13*math.cos(C13)
E28 = F13*math.sin(C13)
E29 = E13
E30 = 1
## J2 FRAME
B33 = math.cos(C14)
B34 = math.sin(C14)
B35 = 0
B36 = 0
C33 = -math.sin(C14)*math.cos(D14)
C34 = math.cos(C14)*math.cos(D14)
C35 = math.sin(D14)
C36 = 0
D33 = math.sin(C14)*math.sin(D14)
D34 = -math.cos(C14)*math.sin(D14)
D35 = math.cos(D14)
D36 = 0
E33 = F14*math.cos(C14)
E34 = F14*math.sin(C14)
E35 = E14
E36 = 1
## J3 FRAME
B39 = math.cos(C15)
B40 = math.sin(C15)
B41 = 0
B42 = 0
C39 = -math.sin(C15)*math.cos(D15)
C40 = math.cos(C15)*math.cos(D15)
C41 = math.sin(D15)
C42 = 0
D39 = math.sin(C15)*math.sin(D15)
D40 = -math.cos(C15)*math.sin(D15)
D41 = math.cos(D15)
D42 = 0
E39 = F15*math.cos(C15)
E40 = F15*math.sin(C15)
E41 = 0
E42 = 1
## J4 FRAME
B45 = math.cos(C16)
B46 = math.sin(C16)
B47 = 0
B48 = 0
C45 = -math.sin(C16)*math.cos(D16)
C46 = math.cos(C16)*math.cos(D16)
C47 = math.sin(D16)
C48 = 0
D45 = math.sin(C16)*math.sin(D16)
D46 = -math.cos(C16)*math.sin(D16)
D47 = math.cos(D16)
D48 = 0
E45 = F16*math.cos(C16)
E46 = F16*math.sin(C16)
E47 = E16
E48 = 1
## J5 FRAME
B51 = math.cos(C17)
B52 = math.sin(C17)
B53 = 0
B54 = 0
C51 = -math.sin(C17)*math.cos(D17)
C52 = math.cos(C17)*math.cos(D17)
C53 = math.sin(D17)
C54 = 0
D51 = math.sin(C17)*math.sin(D17)
D52 = -math.cos(C17)*math.sin(D17)
D53 = math.cos(D17)
D54 = 0
E51 = F17*math.cos(C17)
E52 = F17*math.sin(C17)
E53 = E17
E54 = 1
## J6 FRAME
B57 = math.cos(C18)
B58 = math.sin(C18)
B59 = 0
B60 = 0
C57 = -math.sin(C18)*math.cos(D18)
C58 = math.cos(C18)*math.cos(D18)
C59 = math.sin(D18)
C60 = 0
D57 = math.sin(C18)*math.sin(D18)
D58 = -math.cos(C18)*math.sin(D18)
D59 = math.cos(D18)
D60 = 0
E57 = F18*math.cos(C18)
E58 = F18*math.sin(C18)
E59 = E18
E60 = 1
###################### TOOL FRAME ###########################
###################### Tool coordinate system ############################
B63 = math.cos(math.radians(J18))*math.cos(math.radians(J17))
B64 = math.sin(math.radians(J18))*math.cos(math.radians(J17))
B65 = -math.sin(math.radians(J18))
B66 = 0
C63 = -math.sin(math.radians(J18))*math.cos(math.radians(J16))+math.cos(math.radians(J18))*math.sin(math.radians(J17))*math.sin(math.radians(J16))
C64 = math.cos(math.radians(J18))*math.cos(math.radians(J16))+math.sin(math.radians(J18))*math.sin(math.radians(J17))*math.sin(math.radians(J16))
C65 = math.cos(math.radians(J17))*math.sin(math.radians(J16))
C66 = 0
D63 = math.sin(math.radians(J18))*math.sin(math.radians(J16))+math.cos(math.radians(J18))*math.sin(math.radians(J17))*math.cos(math.radians(J16))
D64 = -math.cos(math.radians(J18))*math.sin(math.radians(J16))+math.sin(math.radians(J18))*math.sin(math.radians(J17))*math.cos(math.radians(J16))
D65 = math.cos(math.radians(J17))*math.cos(math.radians(J16))
D66 = 0
E63 = J13
E64 = J14
E65 = J15
E66 = 1
## WF*J1
G24 = (B21*B27)+(C21*B28)+(D21*B29)+(E21*B30)
G25 = (B22*B27)+(C22*B28)+(D22*B29)+(E22*B30)
G26 = (B23*B27)+(C23*B28)+(D23*B29)+(E23*B30)
G27 = (B24*B27)+(C24*B28)+(D24*B29)+(E24*B30)
H24 = (B21*C27)+(C21*C28)+(D21*C29)+(E21*C30)
H25 = (B22*C27)+(C22*C28)+(D22*C29)+(E22*C30)
H26 = (B23*C27)+(C23*C28)+(D23*C29)+(E23*C30)
H27 = (B24*C27)+(C24*C28)+(D24*C29)+(E24*C30)
I24 = (B21*D27)+(C21*D28)+(D21*D29)+(E21*D30)
I25 = (B22*D27)+(C22*D28)+(D22*D29)+(E22*D30)
I26 = (B23*D27)+(C23*D28)+(D23*D29)+(E23*D30)
I27 = (B24*D27)+(C24*D28)+(D24*D29)+(E24*D30)
J24 = (B21*E27)+(C21*E28)+(D21*E29)+(E21*E30)
J25 = (B22*E27)+(C22*E28)+(D22*E29)+(E22*E30)
J26 = (B23*E27)+(C23*E28)+(D23*E29)+(E23*E30)
J27 = (B24*E27)+(C24*E28)+(D24*E29)+(E24*E30)
## (WF*J1)*J2
G30 = (G24*B33)+(H24*B34)+(I24*B35)+(J24*B36)
G31 = (G25*B33)+(H25*B34)+(I25*B35)+(J25*B36)
G32 = (G26*B33)+(H26*B34)+(I26*B35)+(J26*B36)
G33 = (G27*B33)+(H27*B34)+(I27*B35)+(J27*B36)
H30 = (G24*C33)+(H24*C34)+(I24*C35)+(J24*C36)
H31 = (G25*C33)+(H25*C34)+(I25*C35)+(J25*C36)
H32 = (G26*C33)+(H26*C34)+(I26*C35)+(J26*C36)
H33 = (G27*C33)+(H27*C34)+(I27*C35)+(J27*C36)
I30 = (G24*D33)+(H24*D34)+(I24*D35)+(J24*D36)
I31 = (G25*D33)+(H25*D34)+(I25*D35)+(J25*D36)
I32 = (G26*D33)+(H26*D34)+(I26*D35)+(J26*D36)
I33 = (G27*D33)+(H27*D34)+(I27*D35)+(J27*D36)
J30 = (G24*E33)+(H24*E34)+(I24*E35)+(J24*E36)
J31 = (G25*E33)+(H25*E34)+(I25*E35)+(J25*E36)
J32 = (G26*E33)+(H26*E34)+(I26*E35)+(J26*E36)
J33 = (G27*E33)+(H27*E34)+(I27*E35)+(J27*E36)
## (WF*J1*J2)*J3
G36 = (G30*B39)+(H30*B40)+(I30*B41)+(J30*B42)
G37 = (G31*B39)+(H31*B40)+(I31*B41)+(J31*B42)
G38 = (G32*B39)+(H32*B40)+(I32*B41)+(J32*B42)
G39 = (G33*B39)+(H33*B40)+(I33*B41)+(J33*B42)
H36 = (G30*C39)+(H30*C40)+(I30*C41)+(J30*C42)
H37 = (G31*C39)+(H31*C40)+(I31*C41)+(J31*C42)
H38 = (G32*C39)+(H32*C40)+(I32*C41)+(J32*C42)
H39 = (G33*C39)+(H33*C40)+(I33*C41)+(J33*C42)
I36 = (G30*D39)+(H30*D40)+(I30*D41)+(J30*D42)
I37 = (G31*D39)+(H31*D40)+(I31*D41)+(J31*D42)
I38 = (G32*D39)+(H32*D40)+(I32*D41)+(J32*D42)
I39 = (G33*D39)+(H33*D40)+(I33*D41)+(J33*D42)
J36 = (G30*E39)+(H30*E40)+(I30*E41)+(J30*E42)
J37 = (G31*E39)+(H31*E40)+(I31*E41)+(J31*E42)
J38 = (G32*E39)+(H32*E40)+(I32*E41)+(J32*E42)
J39 = (G33*E39)+(H33*E40)+(I33*E41)+(J33*E42)
## (WF*J1*J2*J3)*J4
G42 = (G36*B45)+(H36*B46)+(I36*B47)+(J36*B48)
G43 = (G37*B45)+(H37*B46)+(I37*B47)+(J37*B48)
G44 = (G38*B45)+(H38*B46)+(I38*B47)+(J38*B48)
G45 = (G39*B45)+(H39*B46)+(I39*B47)+(J39*B48)
H42 = (G36*C45)+(H36*C46)+(I36*C47)+(J36*C48)
H43 = (G37*C45)+(H37*C46)+(I37*C47)+(J37*C48)
H44 = (G38*C45)+(H38*C46)+(I38*C47)+(J38*C48)
H45 = (G39*C45)+(H39*C46)+(I39*C47)+(J39*C48)
I42 = (G36*D45)+(H36*D46)+(I36*D47)+(J36*D48)
I43 = (G37*D45)+(H37*D46)+(I37*D47)+(J37*D48)
I44 = (G38*D45)+(H38*D46)+(I38*D47)+(J38*D48)
I45 = (G39*D45)+(H39*D46)+(I39*D47)+(J39*D48)
J42 = (G36*E45)+(H36*E46)+(I36*E47)+(J36*E48)
J43 = (G37*E45)+(H37*E46)+(I37*E47)+(J37*E48)
J44 = (G38*E45)+(H38*E46)+(I38*E47)+(J38*E48)
J45 = (G39*E45)+(H39*E46)+(I39*E47)+(J39*E48)
## (WF*J1*J2*J3*J4)*J5
G48 = (G42*B51)+(H42*B52)+(I42*B53)+(J42*B54)
G49 = (G43*B51)+(H43*B52)+(I43*B53)+(J43*B54)
G50 = (G44*B51)+(H44*B52)+(I44*B53)+(J44*B54)
G51 = (G45*B51)+(H45*B52)+(I45*B53)+(J45*B54)
H48 = (G42*C51)+(H42*C52)+(I42*C53)+(J42*C54)
H49 = (G43*C51)+(H43*C52)+(I43*C53)+(J43*C54)
H50 = (G44*C51)+(H44*C52)+(I44*C53)+(J44*C54)
H51 = (G45*C51)+(H45*C52)+(I45*C53)+(J45*C54)
I48 = (G42*D51)+(H42*D52)+(I42*D53)+(J42*D54)
I49 = (G43*D51)+(H43*D52)+(I43*D53)+(J43*D54)
I50 = (G44*D51)+(H44*D52)+(I44*D53)+(J44*D54)
I51 = (G45*D51)+(H45*D52)+(I45*D53)+(J45*D54)
J48 = (G42*E51)+(H42*E52)+(I42*E53)+(J42*E54)
J49 = (G43*E51)+(H43*E52)+(I43*E53)+(J43*E54)
J50 = (G44*E51)+(H44*E52)+(I44*E53)+(J44*E54)
J51 = (G45*E51)+(H45*E52)+(I45*E53)+(J45*E54)
## (WF*J1*J2*J3*J4*J5)*J6
G54 = (G48*B57)+(H48*B58)+(I48*B59)+(J48*B60)
G55 = (G49*B57)+(H49*B58)+(I49*B59)+(J49*B60)
G56 = (G50*B57)+(H50*B58)+(I50*B59)+(J50*B60)
G57 = (G51*B57)+(H51*B58)+(I51*B59)+(J51*B60)
H54 = (G48*C57)+(H48*C58)+(I48*C59)+(J48*C60)
H55 = (G49*C57)+(H49*C58)+(I49*C59)+(J49*C60)
H56 = (G50*C57)+(H50*C58)+(I50*C59)+(J50*C60)
H57 = (G51*C57)+(H51*C58)+(I51*C59)+(J51*C60)
I54 = (G48*D57)+(H48*D58)+(I48*D59)+(J48*D60)
I55 = (G49*D57)+(H49*D58)+(I49*D59)+(J49*D60)
I56 = (G50*D57)+(H50*D58)+(I50*D59)+(J50*D60)
I57 = (G51*D57)+(H51*D58)+(I51*D59)+(J51*D60)
J54 = (G48*E57)+(H48*E58)+(I48*E59)+(J48*E60)
J55 = (G49*E57)+(H49*E58)+(I49*E59)+(J49*E60)
J56 = (G50*E57)+(H50*E58)+(I50*E59)+(J50*E60)
J57 = (G51*E57)+(H51*E58)+(I51*E59)+(J51*E60)
## (WF*J1*J2*J3*J4*J5*J6)*TF
G60 = (G54*B63)+(H54*B64)+(I54*B65)+(J54*B66)
G61 = (G55*B63)+(H55*B64)+(I55*B65)+(J55*B66)
G62 = (G56*B63)+(H56*B64)+(I56*B65)+(J56*B66)
G63 = (G57*B63)+(H57*B64)+(I57*B65)+(J57*B66)
H60 = (G54*C63)+(H54*C64)+(I54*C65)+(J54*C66)
H61 = (G55*C63)+(H55*C64)+(I55*C65)+(J55*C66)
H62 = (G56*C63)+(H56*C64)+(I56*C65)+(J56*C66)
H63 = (G57*C63)+(H57*C64)+(I57*C65)+(J57*C66)
I60 = (G54*D63)+(H54*D64)+(I54*D65)+(J54*D66)
I61 = (G55*D63)+(H55*D64)+(I55*D65)+(J55*D66)
I62 = (G56*D63)+(H56*D64)+(I56*D65)+(J56*D66)
I63 = (G57*D63)+(H57*D64)+(I57*D65)+(J57*D66)
J60 = (G54*E63)+(H54*E64)+(I54*E65)+(J54*E66)
J61 = (G55*E63)+(H55*E64)+(I55*E65)+(J55*E66)
J62 = (G56*E63)+(H56*E64)+(I56*E65)+(J56*E66)
J63 = (G57*E63)+(H57*E64)+(I57*E65)+(J57*E66)边栏推荐
- Bugku's Eval
- Ten billion massage machine blue ocean, difficult to be a giant
- sql server学习笔记
- P1451 calculate the number of cells / 1329: [example 8.2] cells
- The difference between abstract classes and interfaces in PHP (PHP interview theory question)
- SQL Server learning notes
- Redis distributed lock principle and its implementation with PHP (1)
- Misc Basic test method and knowledge points of CTF
- Common PHP interview questions (1) (written PHP interview questions)
- wxml2canvas
猜你喜欢
具有倍数关系的时钟切换
RepLKNet:不是大卷积不好,而是卷积不够大,31x31卷积了解一下 | CVPR 2022
Data communication foundation smart_ Link_&_ Monitor_ Link
【簡記】解决IDE golang 代碼飄紅報錯
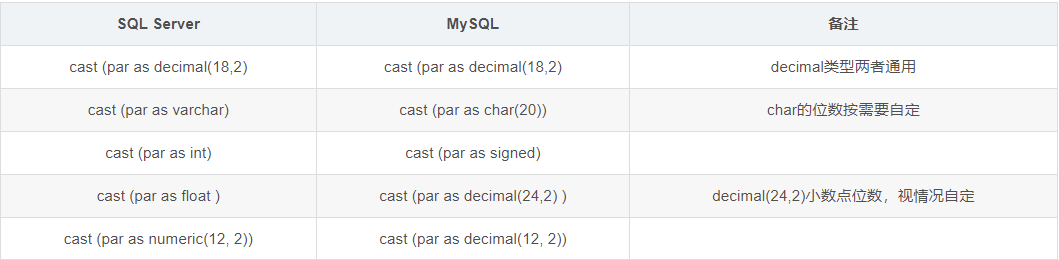
sql server学习笔记
![[brief notes] solve the problem of IDE golang code red and error reporting](/img/b6/0b2ea06eb5fbe651ff9247b109fa15.png)
[brief notes] solve the problem of IDE golang code red and error reporting

Example of lvgl display picture
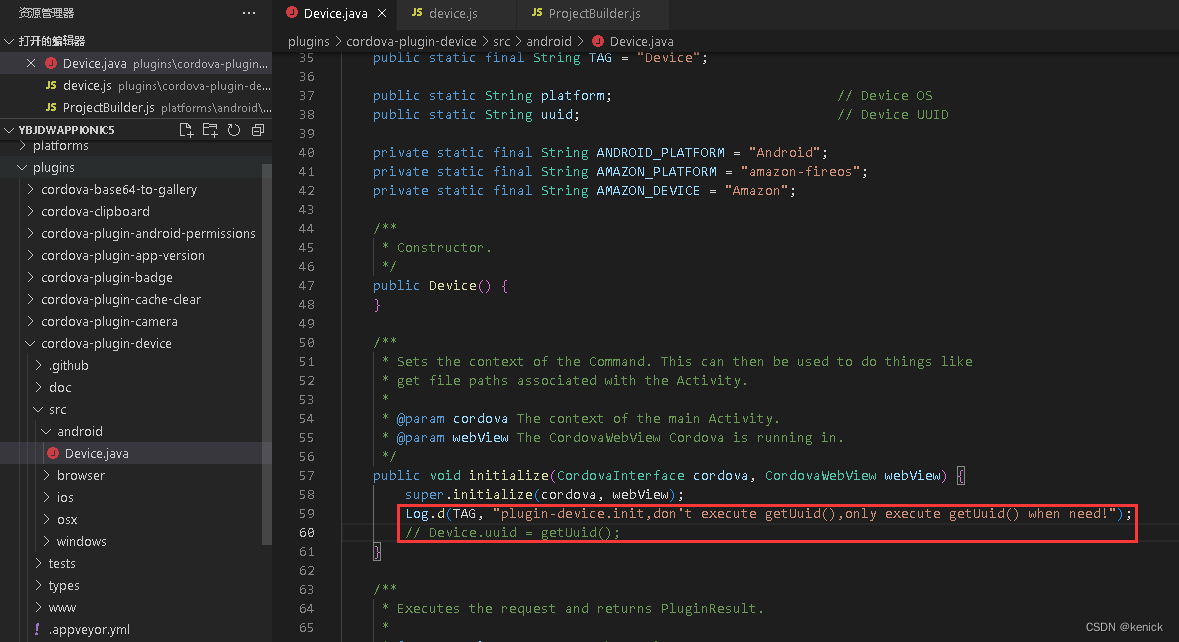
Ionic Cordova project modification plug-in
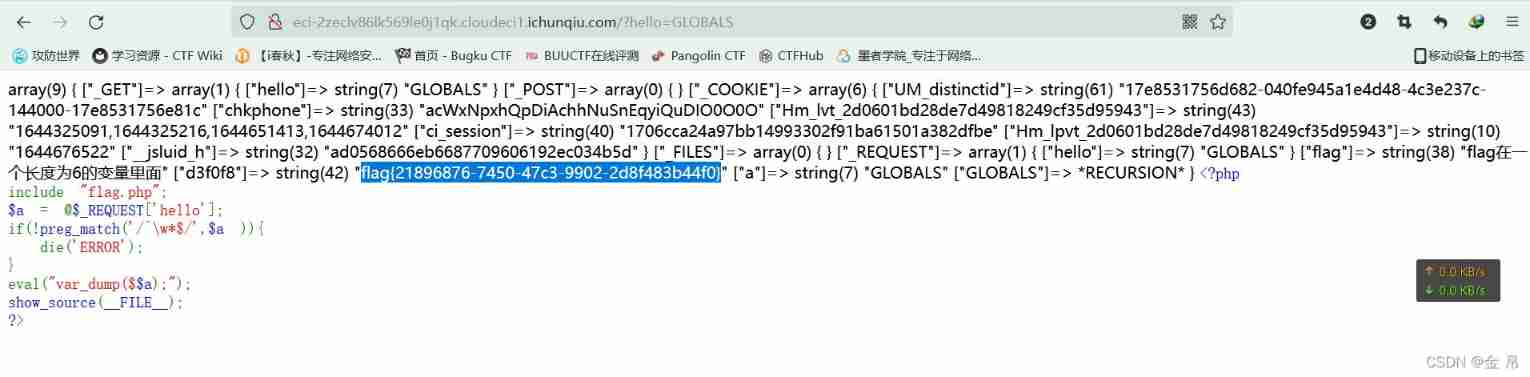
I spring and autumn blasting-1
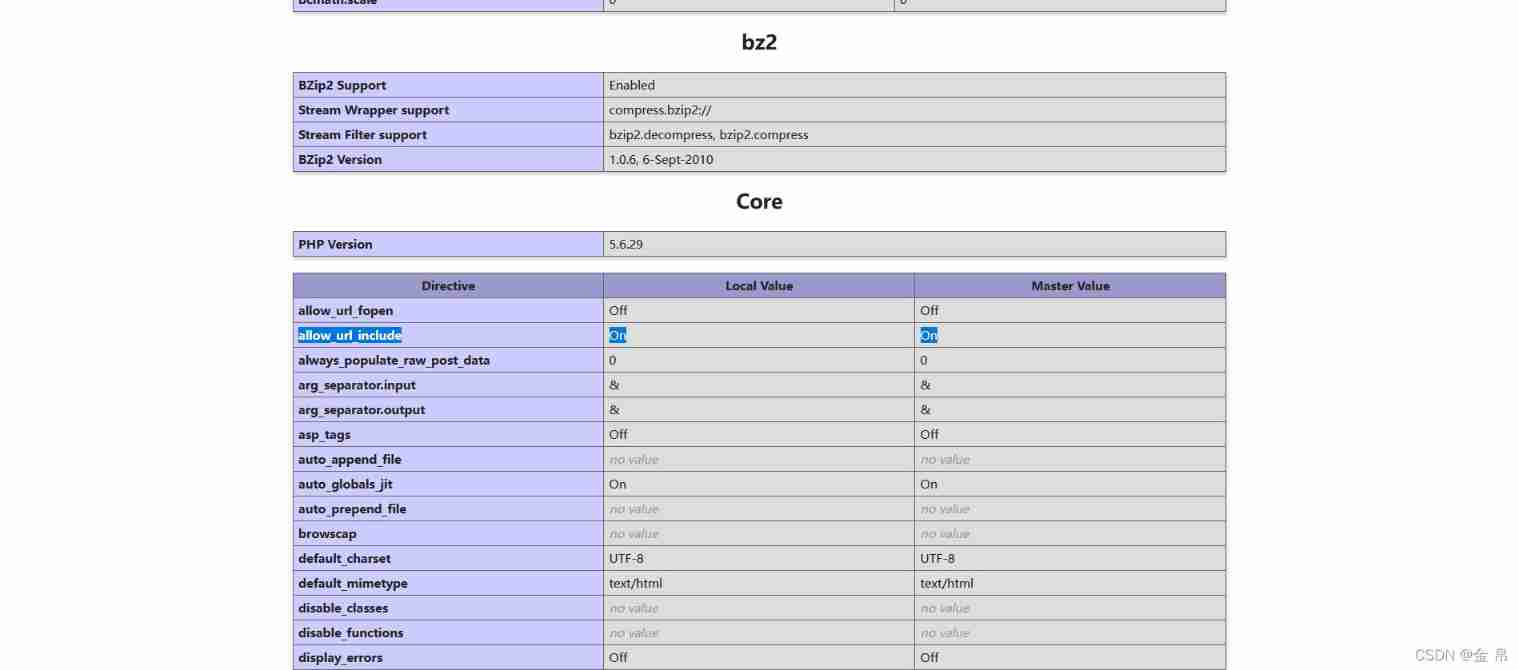
I include of spring and Autumn
随机推荐
Explanation report of the explosion
Hongmeng system -- Analysis from the perspective of business
Redis' transaction mechanism
2.3 learning content
queryRunner. Query method
18.[STM32]读取DS18B20温度传感器的ROM并实现多点测量温度
Data communication foundation - route republication
Can I pass the PMP Exam in 20 days?
【 note 】 résoudre l'erreur de code IDE golang
Noi / 1.3 01: a+b problem
六种常用事务解决方案,你方唱罢,我登场(没有最好只有更好)
Fundamentals of data communication - Principles of IP routing
Definition of episodic and batch
String modification problem solving Report
Codasip为RISC-V处理器系列增加Veridify安全启动功能
Interval DP (gravel consolidation)
16.[STM32]从原理开始带你了解DS18B20温度传感器-四位数码管显示温度
MySQL giant pit: update updates should be judged with caution by affecting the number of rows!!!
No one consults when doing research and does not communicate with students. UNC assistant professor has a two-year history of teaching struggle
verilog实现计算最大公约数和最小公倍数