当前位置:网站首页>[Blue Bridge Cup 2017 preliminary] buns make up
[Blue Bridge Cup 2017 preliminary] buns make up
2022-07-06 11:25:00 【%xiao Q】
subject
Title Description
Xiao Ming has breakfast in a bun shop almost every morning . This bun shop has N Grow steamer , Among them the first i The kind of steamer can put Ai A steamed bun
Each kind of steamer has a lot of steamers , It can be thought of as an infinite cage .
Whenever a customer wants to buy X A steamed bun , Uncle will choose some steamed buns , So that these cages happen to have X A steamed bun .
Let's say there are 3 Grow steamer , You can put 3、4 and 5 A steamed bun . When customers want to buy 11 A bun , Uncle will choose 2 Cage 3 One more 1 Cage 5 One of the ( It is also possible to elect 1 Cage 3 One more 2 Cage 4 One of the ).
Of course, sometimes uncle baozi can't figure out the quantity customers want to buy .
Let's say there are 3 Grow steamer , You can put 4、5 and 6 A steamed bun . And customers want to buy 7 A bun , Uncle can't make it out .
Xiao Ming wants to know how many kinds of numbers can't be found by Uncle baozi .
Input format
The first line contains an integer N.(1 <= N <= 100)
following N Each line contains an integer Ai.(1 <= Ai <= 100)
Output format
The output line contains an integer to represent the answer . If you can't figure out an infinite number , Output INF.
sample input Copy
2
4
5
sample output Copy
6
Data range and tips
For example , The uncountable number includes :1, 2, 3, 6, 7, 11.
analysis :
This problem needs to know a theorem , Euclidean theorem : For not completely 0 The integer of a,b So there must be integers x,y bring gcd(x,y) = a * x + b * y.
So we can assume that a * x + b * y = d, To make the equation solvable , that d % gcd(a, b) = 0 It is inevitable , If gcd(a,b) = 1, that d Can divide any number , That is to say a,b this 2 Any number can be divided by numbers ( But there can't be negative numbers in it , So there are some numbers that cannot be summed up ), On the contrary, we can't .
So the first step is to find the greatest common divisor of these numbers , If gcd = 1, Then how many numbers can't be summed up in the judgment , If gcd != 1, Then there must be countless kinds of numbers that can't be summed up , Direct output INF.
Reference code :
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 10010, M = 110;
int f[N];
int a[N];
int main()
{
int n;
cin >> n;
int g = 0;
rep(i, 1, n)
{
cin >> a[i];
g = __gcd(g, a[i]);
}
if(g != 1)
{
puts("INF");
return 0;
}
rep(i, 1, n) f[a[i]] = 1;
rep(i, 1, n)
for(int j = 0; j + a[i]<= 10000; j++) // Here to 10000 It's a little metaphysical ( mathematics , No )
{
if(f[j]) f[j + a[i]] = 1;
}
int ans = 0;
rep(i, 1, 10000)
if(!f[i]) ans++;
cout << ans << endl;
return 0;
}
边栏推荐
- 数数字游戏
- About string immutability
- Ansible practical series I_ introduction
- [AGC009D]Uninity
- Tcp/ip protocol (UDP)
- 图片上色项目 —— Deoldify
- Codeforces Round #753 (Div. 3)
- 基于apache-jena的知识问答
- When you open the browser, you will also open mango TV, Tiktok and other websites outside the home page
- How to configure flymcu (STM32 serial port download software) is shown in super detail
猜你喜欢

PHP - whether the setting error displays -php xxx When PHP executes, there is no code exception prompt
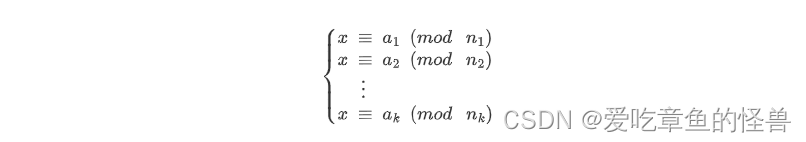
AcWing 1298. Solution to Cao Chong's pig raising problem
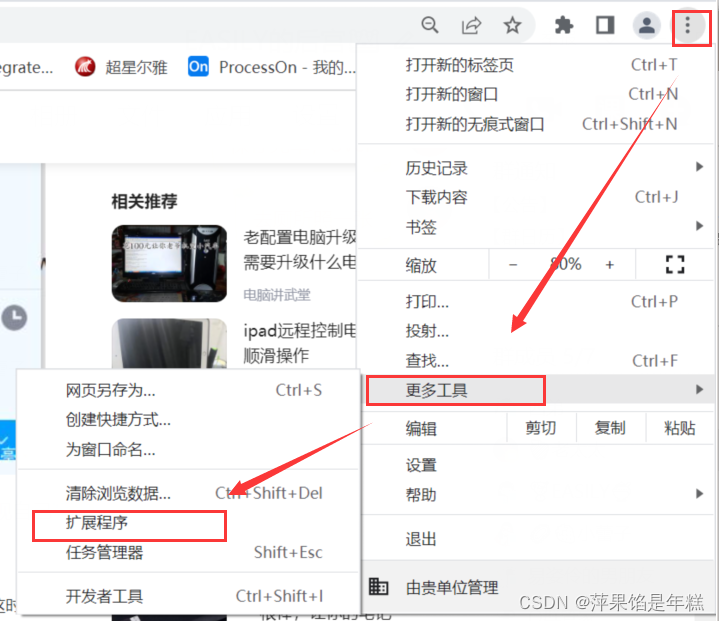
When you open the browser, you will also open mango TV, Tiktok and other websites outside the home page
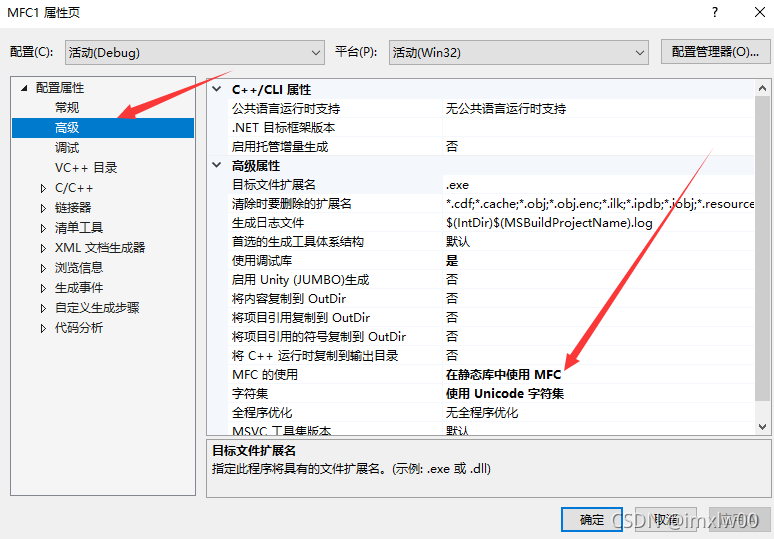
Vs2019 first MFC Application
Reading BMP file with C language

AcWing 242. A simple integer problem (tree array + difference)
![[蓝桥杯2017初赛]方格分割](/img/e9/e49556d0867840148a60ff4906f78e.png)
[蓝桥杯2017初赛]方格分割
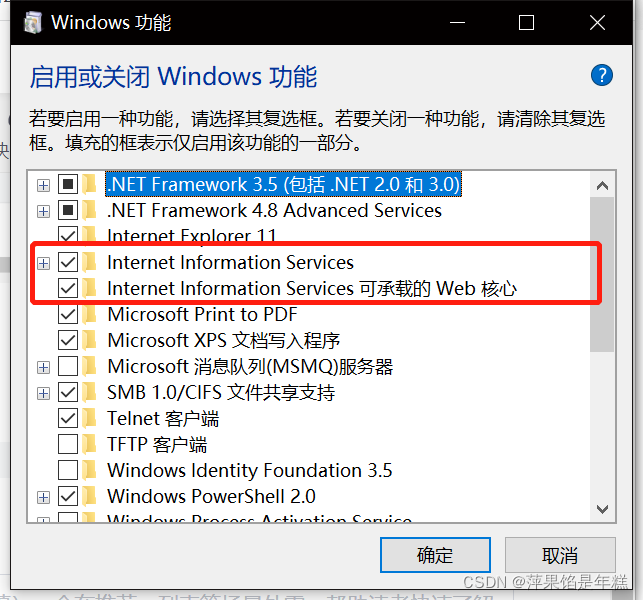
学习问题1:127.0.0.1拒绝了我们的访问
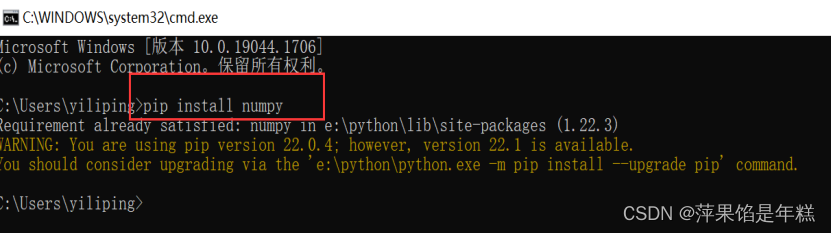
安装numpy问题总结
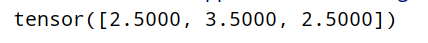
Pytorch基础
随机推荐
Codeforces Round #753 (Div. 3)
MySQL and C language connection (vs2019 version)
数据库高级学习笔记--SQL语句
Aborted connection 1055898 to db:
图像识别问题 — pytesseract.TesseractNotFoundError: tesseract is not installed or it‘s not in your path
Number game
Learning question 1:127.0.0.1 refused our visit
Machine learning -- census data analysis
Software testing and quality learning notes 3 -- white box testing
记一次某公司面试题:合并有序数组
Principes JDBC
Ansible practical series I_ introduction
QT creator uses Valgrind code analysis tool
Database advanced learning notes -- SQL statement
QT creator custom build process
vs2019 桌面程序快速入门
Test objects involved in safety test
AI benchmark V5 ranking
AcWing 179.阶乘分解 题解
[ahoi2009]chess Chinese chess - combination number optimization shape pressure DP