LeetCode 1557. The minimum number of points that can reach all points

1557. The minimum number of points that can reach all points

To give you one Directed acyclic graph , n Node number is 0 To n-1 , And an array of edges edges , among edges[i] = [fromi, toi] Represents a slave point fromi point-to-point toi The directed side of .

Find the smallest set of points so that all points in the graph can be reached from these points . The problem guarantees that the solution exists and is unique .

You can return these node numbers in any order .

Example 1：

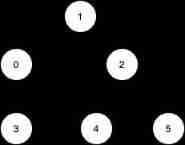
 Input ：n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
 Output ：[0,3]
 explain ： All nodes cannot be reached from a single node . from  0  We can get to  [0,1,2,5] . from  3  We can get to  [3,4,2,5] . So we output  [0,3] .

Example 2：

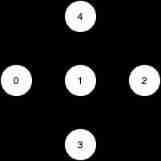
 Input ：n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
 Output ：[0,2,3]
 explain ： Note the node  0,3  and  2  Unable to reach... From other nodes , So we have to include them in the result point set , These points can reach the node  1  and  4 .

Tips ：

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• All point pairs (fromi, toi) Different from each other .

Two 、 Method 1

Looking for penetration 0 The node of is

class Solution {
    
    public List<Integer> findSmallestSetOfVertices(int n, List<List<Integer>> edges) {
    
        List<Integer> res = new ArrayList<>();
        Set<Integer> set = new HashSet<>();
        for (List<Integer> edge : edges) {
    
            set.add(edge.get(1));
        }
        for (int i = 0; i < n; i++) {
    
            if (!set.contains(i)) {
    
                res.add(i);
            }
        }
        return res;
    }
}

Complexity analysis

• Time complexity ：O(m+n), among m Is the number of edges in the graph ,n Is the number of nodes in the graph . You need to traverse all the edges to get nodes with non-zero penetration , Then traverse all nodes and keep the nodes with zero penetration .

• Spatial complexity ：O(n), among n Is the number of nodes in the graph . You need to use a collection to store nodes with non-zero penetration , The number of nodes in the collection will not exceed n.