当前位置:网站首页>Detailed explanation of diffusion model
Detailed explanation of diffusion model
2022-07-07 09:40:00 【Ghost road 2022】
1 introduction
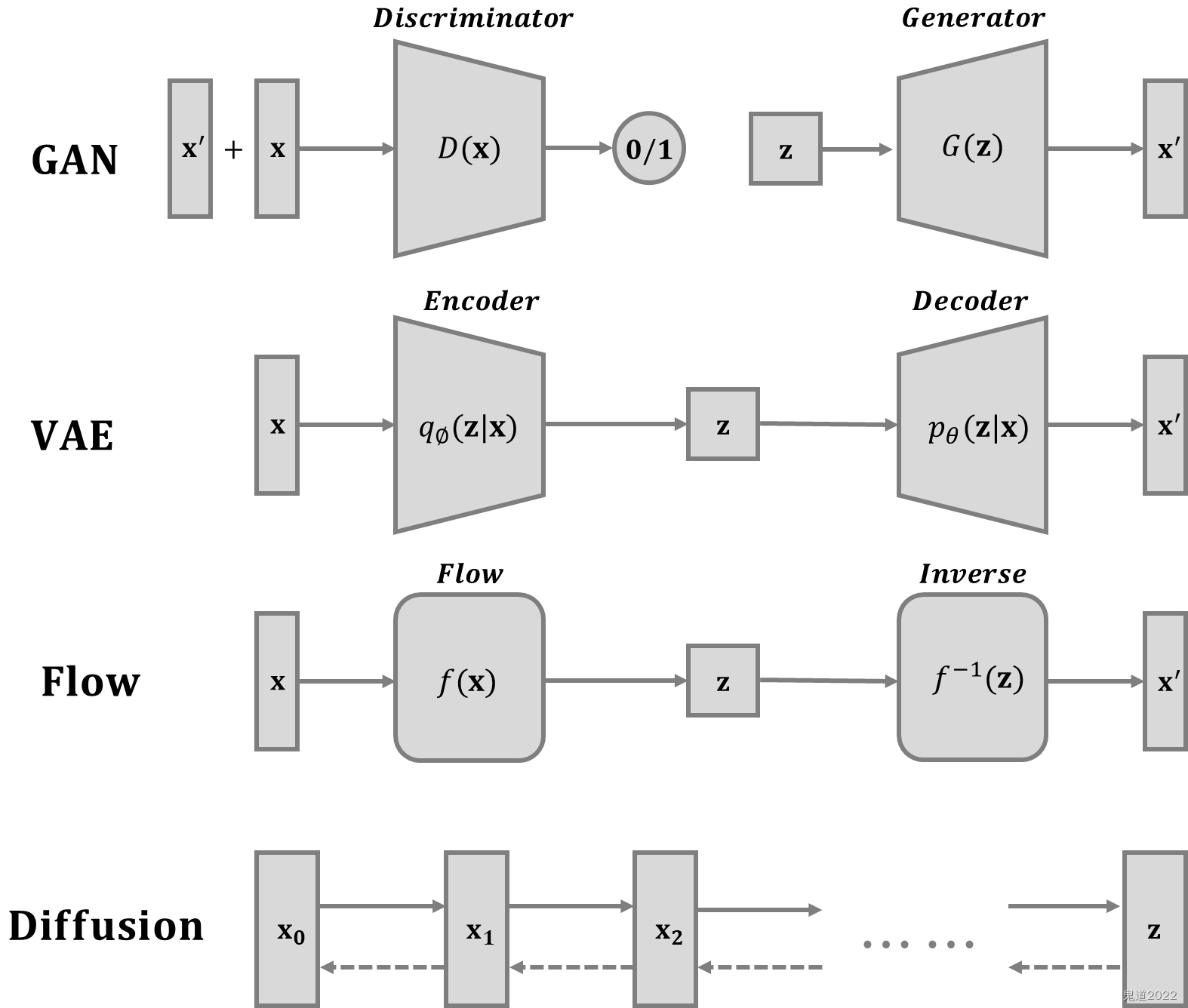
In the last article 《 Depth generation model based on flow 》 The theory and method of flow generation model are introduced in detail . So far, , be based on GAN Generate models , be based on VAE The generation model of , And based on flow All of them can generate high-quality samples , But each method has its limitations .GAN In the process of confrontation training, there will be problems of mode collapse and unstable training ;VAE It depends heavily on the target loss function ; The flow model must use a special framework to build reversible transformations . This paper mainly introduces the diffusion model , Its inspiration comes from non-equilibrium thermodynamics . They define Markov chains of diffusion steps , Slowly add random noise to the data , Then learn the reverse diffusion process to construct the required data samples from the noise . And VAE Or different flow models , The diffusion model is learned through a fixed process , And the hidden variables in the middle have high dimensions with the original data .
- advantage : The diffusion model is both easy to analyze and flexible . Be aware that manageability and flexibility are two conflicting goals in Generative modeling . Easy to handle models can be used to analyze, evaluate and fit data , But they cannot easily describe the structure of rich data sets . The flexible model can fit any structure in the data , But evaluate from these models 、 The cost of training or sampling can be high .
- shortcoming : The diffusion model relies on a long Markov diffusion step chain to generate samples , Therefore, the cost in terms of time and calculation will be very high . At present, new methods have been proposed to make the process faster , But the overall process of sampling is still better than GAN slow .
2 Forward diffusion process
Given the distribution from real data x 0 ∼ q ( x ) {\bf{x}}_0\sim q({\bf{x}}) x0∼q(x) Data points sampled in , In a forward diffusion process , stay T T T Step by step, add a small amount of Gaussian noise to the sample , Thus, a series of noise samples are generated x 1 , ⋯ , x T {\bf{x}}_1,\cdots,{\bf{x}}_T x1,⋯,xT, Its step length is planned by variance { β t ∈ ( 0 , 1 ) } t = 1 T \{\beta_t\in(0,1)\}_{t=1}^T { βt∈(0,1)}t=1T To control , Then there are q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β x t − 1 , β t I ) q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) q({\bf{x}}_t|{\bf{x}}_{t-1})=\mathcal{N}({\bf{x}}_t;\sqrt{1-\beta}{\bf{x}}_{t-1},\beta_t {\bf{I}})\quad q({\bf{x}}_{1:T}|{\bf{x}}_0)=\prod_{t=1}^Tq({\bf{x}}_t|{\bf{x}}_{t-1}) q(xt∣xt−1)=N(xt;1−βxt−1,βtI)q(x1:T∣x0)=t=1∏Tq(xt∣xt−1) During the diffusion process , With the time step t t t The increase of , Data samples x 0 {\bf{x}}_0 x0 Gradually lose its distinguishing features . Final , When T → ∞ T\rightarrow \infty T→∞, x T {\bf{x}}_T xT Equivalent to isotropic Gaussian distribution ( Isotropic Gaussian distribution is called spherical Gaussian distribution , In particular, it refers to the multi-dimensional Gaussian distribution with the same variance in all directions , The covariance is a positive real number multiplied by the identity matrix ).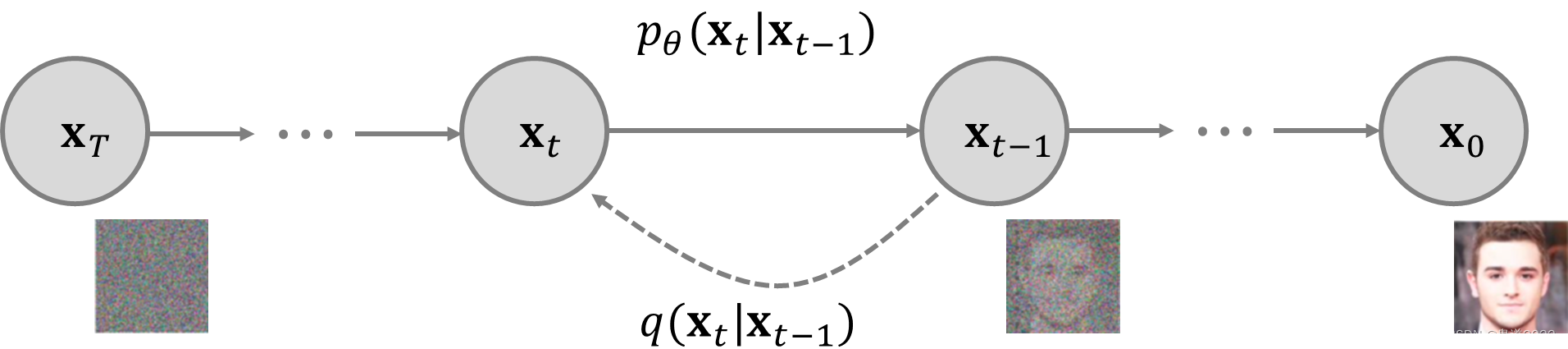
A good feature of the above process is that the reparameterization technique can be used in a closed form at any time step t t t Yes x t {\bf{x}}_t xt sampling . Make α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt and α ˉ t = ∏ i = 1 T α i \bar{\alpha}_t=\prod_{i=1}^T \alpha_i αˉt=∏i=1Tαi, Then there are : x t = α t x t − 1 + 1 − α t z t − 1 = α t α t − 1 x t − 2 + 1 − α t α t − 1 z ˉ t − 2 = ⋯ = α ˉ t x 0 + 1 − α ˉ t z q ( x t ∣ x 0 ) = N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) \begin{aligned}{\bf{x}}_t&=\sqrt{\alpha_t}{\bf{x}}_{t-1}+\sqrt{1-\alpha_t}{\bf{z}}_{t-1}\\&=\sqrt{\alpha_t\alpha_{t-1}}{\bf{x}}_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}{\bf{\bar{z}}}_{t-2}\\&=\cdots\\&=\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}{\bf{z}}\\q({\bf{x}}_t|{\bf{x}}_0)&=\mathcal{N}({\bf{x}}_t;\sqrt{\bar{\alpha}_t}{\bf{x}}_0,(1-\bar{\alpha}_t){\bf{I}})\end{aligned} xtq(xt∣x0)=αtxt−1+1−αtzt−1=αtαt−1xt−2+1−αtαt−1zˉt−2=⋯=αˉtx0+1−αˉtz=N(xt;αˉtx0,(1−αˉt)I) among z t − 1 , z t − 2 , ⋯ ∼ N ( 0 , I ) {\bf{z}}_{t-1},{\bf{z}}_{t-2},\cdots \sim\mathcal{N}({\bf{0}},{\bf{I}}) zt−1,zt−2,⋯∼N(0,I), z ˉ t − 2 {\bar{\bf{z}}}_{t-2} zˉt−2 Fuse two Gaussian distributions . When merging two with different variances N ( 0 , σ 1 2 I ) \mathcal{N}({\bf{0}},\sigma^2_1{\bf{I}}) N(0,σ12I) and N ( 0 , σ 2 2 I ) \mathcal{N}({\bf{0}},\sigma^2_2{\bf{I}}) N(0,σ22I) When the Gaussian distribution of , The new Gaussian distribution obtained is N ( 0 , ( σ 1 2 , σ 2 2 ) I ) \mathcal{N}({\bf{0}},(\sigma^2_1,\sigma_2^2){\bf{I}}) N(0,(σ12,σ22)I), The combined standard deviation is ( 1 − α t ) + α t ( 1 − α t − 1 ) = 1 − α t α t − 1 \sqrt{(1-\alpha_t)+\alpha_t(1-\alpha_{t-1})}=\sqrt{1-\alpha_{t}\alpha_{t-1}} (1−αt)+αt(1−αt−1)=1−αtαt−1 Usually , The larger the noise is, the larger the update step will be , Then there are β 1 < β 2 ⋯ < β T \beta_1<\beta_2\cdots<\beta_T β1<β2⋯<βT, therefore α ˉ 1 > ⋯ > α ˉ T \bar{\alpha}_1>\cdots>\bar{\alpha}_T αˉ1>⋯>αˉT.
3 The update process
Langevin Dynamics is a concept in Physics , For statistical modeling of molecular systems . Combined with random gradient descent , Random gradient Langevin dynamics can only use the gradient in the Markov update chain ∇ x log p ( x ) \nabla_{\bf{x}} \log p({\bf{x}}) ∇xlogp(x) From the probability density p ( x ) p({\bf{x}}) p(x) Generated samples : x t = x t − 1 + ϵ 2 ∇ x log p ( x t − 1 ) + ϵ z t , z t ∼ N ( 0 , I ) {\bf{x}}_t={\bf{x}}_{t-1}+\frac{\epsilon}{2}\nabla_{\bf{x}} \log p({\bf{x}}_{t-1})+\sqrt{\epsilon}{\bf{z}}_t,\quad {\bf{z}}_t\sim\mathcal{N}({\bf{0}},{\bf{I}}) xt=xt−1+2ϵ∇xlogp(xt−1)+ϵzt,zt∼N(0,I) among ϵ \epsilon ϵ Step length . When T → ∞ T\rightarrow \infty T→∞ when , ϵ → 0 \epsilon\rightarrow 0 ϵ→0, x {\bf{x}} x_T Is equal to the true probability density p ( x ) p({\bf{x}}) p(x). With the standard SGD comparison , Random gradient Langevin Dynamics injects Gaussian noise into parameter update , To avoid falling into the local minimum .
4 Reverse diffusion process
If the above process is reversed and the probability distribution q ( x t − 1 ∣ x t ) q({\bf{x}}_{t-1}|{\bf{x}}_t) q(xt−1∣xt) Sampling in , Can be input from Gaussian noise x T ∼ N ( 0 , I ) {\bf{x}}_T\sim \mathcal{N}({\bf{0}},{\bf{I}}) xT∼N(0,I) Reconstruct the real sample . It should be noted that if β t \beta_t βt Small enough , q ( x t − 1 , x t ) q({\bf{x}}_{t-1},{\bf{x}}_t) q(xt−1,xt) It will also be Gaussian distribution . But this needs to be estimated using the entire data set , So we need to learn a model p θ p_\theta pθ To approximate these conditional probabilities , In order to carry out the reverse diffusion process p θ ( x 0 : T ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta({\bf{x}}_{0:T})=p({\bf{x}}_T)\prod_{t=1}^T p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)\quad p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)=\mathcal{N}({\bf{x}}_{t-1};\boldsymbol{\mu}_\theta({\bf{x}}_t,t),{ {\bf{\Sigma}}_\theta({\bf{x}}_t,t)}) pθ(x0:T)=p(xT)t=1∏Tpθ(xt−1∣xt)pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)) When conditions are x 0 {\bf{x}}_0 x0 when , The inverse conditional probability is easy to estimate : q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ( x t , x 0 ) , β ~ t I ) q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)=\mathcal{N}({\bf{x}}_{t-1};\boldsymbol{\mu}({\bf{x}}_t,{\bf{x}}_0),\tilde{\beta}_t{\bf{I}}) q(xt−1∣xt,x0)=N(xt−1;μ(xt,x0),β~tI) Using Bayesian law, we can get q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) ∝ exp [ − 1 2 ( ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ] = exp [ − 1 2 ( x t 2 − 2 α t x t x t − 1 + α t x t − 1 2 β t + x t − 1 2 − 2 α ˉ t − 1 x 0 x t − 1 + α ˉ t − 1 x 0 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ] = exp [ − 1 2 ( ( α t β t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ) ] \begin{aligned}q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)&=q({\bf{x}}_{t}|{\bf{x}}_{t-1},{\bf{x}}_0)\frac{q({\bf{x}}_{t-1}|{\bf{x}}_0)}{q({\bf{x}}_t|{\bf{x}}_0)}\\&\propto\exp\left[-\frac{1}{2}\left(\frac{({\bf{x}}_t-\sqrt{\alpha_t}{\bf{x}}_{t-1})^2}{\beta_t}+\frac{({\bf{x}}_{t-1}-\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0)^2}{1-\bar{\alpha}_{t-1}}-\frac{({\bf{x}}_t-\sqrt{\bar{\alpha}_t}{\bf{x}}_0)^2}{1-\bar{\alpha}_t}\right)\right]\\&=\exp\left[-\frac{1}{2}\left(\frac{ {\bf{x}}^2_t-2\sqrt{\alpha_t}{\bf{x}}_t{\bf{x}}_{t-1}+\alpha_t{\bf{x}}_{t-1}^2}{\beta_t}+\frac{ {\bf{x}}_{t-1}^2-2\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0{\bf{x}}_{t-1}+\bar{\alpha}_{t-1}{\bf{x}}_0}{1-\bar{\alpha}_{t-1}}-\frac{({\bf{x}}_t-\sqrt{\bar{\alpha}_t}{\bf{x}}_0)^2}{1-\bar{\alpha}_t}\right)\right]\\&=\exp\left[-\frac{1}{2}\left(\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right){\bf{x}}^2_{t-1}-\left(\frac{2\sqrt{\alpha_t}}{\beta_t}{\bf{x}}_t+\frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}{\bf{x}}_0\right){\bf{x}}_{t-1}+C({\bf{x}}_t,{\bf{x}}_0)\right)\right]\end{aligned} q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)∝exp[−21(βt(xt−αtxt−1)2+1−αˉt−1(xt−1−αˉt−1x0)2−1−αˉt(xt−αˉtx0)2)]=exp[−21(βtxt2−2αtxtxt−1+αtxt−12+1−αˉt−1xt−12−2αˉt−1x0xt−1+αˉt−1x0−1−αˉt(xt−αˉtx0)2)]=exp[−21((βtαt+1−αˉt−11)xt−12−(βt2αtxt+1−αˉt−12αˉt−1x0)xt−1+C(xt,x0))] among C ( x t , x 0 ) C({\bf{x}}_t,{\bf{x}}_0) C(xt,x0) Function and x t − 1 {\bf{x}}_{t-1} xt−1 irrelevant . According to the standard Gaussian density function , The mean and variance can be parameterized as follows β ~ t = 1 / ( α t β t + 1 1 − α ˉ t − 1 ) = 1 / ( α t − α ˉ t + β t β t ( 1 − α ˉ t − 1 ) ) = 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t μ ~ t ( x t , x 0 ) = ( α t β t x t + α ˉ t − 1 1 − α ˉ t − 1 x 0 ) / ( α t β t + 1 1 − α ˉ t − 1 ) = ( α t β t x t + α ˉ t − 1 1 − α ˉ t − 1 x 0 ) 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \begin{aligned}\tilde{\beta}_t&=1\left/\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)\right.=1\left/\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t(1-\bar{\alpha}_{t-1})}\right)\right.=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot \beta_t\\\tilde{\boldsymbol{\mu}}_t({\bf{x}}_t,{\bf{x}}_0)&=\left(\frac{\sqrt{\alpha}_t}{\beta_t}{\bf{x}}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}{\bf{x}}_0\right)\left/\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)\right.\\&=\left(\frac{\sqrt{\alpha}_t}{\beta_t}{\bf{x}}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}{\bf{x}}_0\right)\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot\beta_t\\&=\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}{\bf{x}}_t+\frac{\sqrt{\bar{\alpha}_{t-1}\beta_t}}{1-\bar{\alpha}_t}{\bf{x}}_0\end{aligned} β~tμ~t(xt,x0)=1/(βtαt+1−αˉt−11)=1/(βt(1−αˉt−1)αt−αˉt+βt)=1−αˉt1−αˉt−1⋅βt=(βtαtxt+1−αˉt−1αˉt−1x0)/(βtαt+1−αˉt−11)=(βtαtxt+1−αˉt−1αˉt−1x0)1−αˉt1−αˉt−1⋅βt=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtx0 take x 0 = 1 α ˉ t ( x t − 1 − α ˉ t z t ) {\bf{x}}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}({\bf{x}}_t-\sqrt{1-\bar{\alpha}_t}{\bf{z}}_t) x0=αˉt1(xt−1−αˉtzt) Brought into the above formula is μ ~ t = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t 1 α ˉ t ( x t − 1 − α ˉ t z t ) = 1 α t ( x t − β t 1 − α ˉ t z t ) \begin{aligned}\boldsymbol{\tilde{\mu}}_t&=\frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}{\bf{x}}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1-\bar{\alpha}_t}\frac{1}{\sqrt{\bar{\alpha}_t}}({\bf{x}}_t-\sqrt{1-\bar{\alpha}_t}{\bf{z}}_t)\\&=\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}{\bf{z}}_t\right)\end{aligned} μ~t=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1βtαˉt1(xt−1−αˉtzt)=αt1(xt−1−αˉtβtzt) This setting is similar to VAE Very similar , Therefore, the variational lower bound can be used to optimize the negative log likelihood , Then there are − log p θ ( x 0 ) ≤ − log p θ ( x 0 ) + D K L ( q ( x 1 : T ) ∣ x 0 ∣ ∣ p θ ( x 1 : T ∣ x 0 ) ) = − log p θ ( x θ ) + E 1 : T ∼ q ( x 1 : T ∣ x 0 ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) / p θ ( x 0 ) ] = − log p θ ( x 0 ) + E q [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) + log p θ ( x 0 ) ] = E q [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] L V L B = E q ( x 0 : T ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] ≥ − E q ( x 0 ) log p θ ( x 0 ) \begin{aligned}-\log p_\theta({\bf{x}}_0)&\le -\log p_\theta({\bf{x}}_0)+D_{\mathrm{KL}}(q({\bf{x}}_{1:T})|{\bf{x}}_0||p_\theta({\bf{x}}_{1:T}|{\bf{x}}_0))\\&=-\log p_\theta({\bf{x}}_\theta)+\mathbb{E}_{1:T\sim q({\bf{x}}_{1:T}|{\bf{x}}_0)}\left[\log \frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})/p_\theta({\bf{x}}_0)}\right]\\&=-\log p_\theta({\bf{x}}_0)+\mathbb{E}_q\left[\log \frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})}+\log p_\theta ({\bf{x}}_0)\right]\\&=\mathbb{E}_q\left[\log \frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})}\right]\\L_{\mathrm{VLB}}&=\mathbb{E}_{q({\bf{x}}_{0:T})}\left[\log \frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})}\right]\ge -\mathbb{E}_{q({\bf{x}}_0)}\log p_\theta({\bf{x}}_0)\end{aligned} −logpθ(x0)LVLB≤−logpθ(x0)+DKL(q(x1:T)∣x0∣∣pθ(x1:T∣x0))=−logpθ(xθ)+E1:T∼q(x1:T∣x0)[logpθ(x0:T)/pθ(x0)q(x1:T∣x0)]=−logpθ(x0)+Eq[logpθ(x0:T)q(x1:T∣x0)+logpθ(x0)]=Eq[logpθ(x0:T)q(x1:T∣x0)]=Eq(x0:T)[logpθ(x0:T)q(x1:T∣x0)]≥−Eq(x0)logpθ(x0) Use Jensen Inequality can easily get the same result . Suppose we want to minimize cross entropy as the learning goal , Then there are L C E = − E q ( x 0 ) log p θ ( x 0 ) = − E q ( x 0 ) log ( ∫ p θ ( x 0 : T ) d x 1 : T ) = − E q ( x 0 ) log ( ∫ q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) d x 1 : T ) = − E q ( x 0 ) log ( E q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) ≤ − E q ( x 0 : T ) log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) = E q ( x 0 : T ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] = L V T B \begin{aligned}L_{\mathrm{CE}}&=-\mathbb{E}_{q({\bf{x}}_0)}\log p_\theta({\bf{x}}_0)\\&=-\mathbb{E}_{q({\bf{x}}_0)}\log\left(\int p_\theta({\bf{x}}_{0:T})d {\bf{x}}_{1:T}\right)\\&=-\mathbb{E}_{q({\bf{x}}_0)}\log\left(\int q({\bf{x}}_{1:T}|{\bf{x}}_0)\frac{p_\theta({\bf{x}}_{0:T})}{q({\bf{x}}_{1:T}|{\bf{x}}_0)}d{\bf{x}}_{1:T}\right)\\&=-\mathbb{E}_{q({\bf{x}}_0)}\log\left(\mathbb{E}_{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\frac{p_\theta({\bf{x}}_{0:T})}{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\right)\\ &\le -\mathbb{E}_{q({\bf{x}}_{0:T})}\log\frac{p_\theta({\bf{x}}_{0:T})}{q({\bf{x}}_{1:T}|{\bf{x}}_0)}\\&=\mathbb{E}_{q({\bf{x}}_{0:T})}\left[\log\frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})}\right]=L_{\mathrm{VTB}}\end{aligned} LCE=−Eq(x0)logpθ(x0)=−Eq(x0)log(∫pθ(x0:T)dx1:T)=−Eq(x0)log(∫q(x1:T∣x0)q(x1:T∣x0)pθ(x0:T)dx1:T)=−Eq(x0)log(Eq(x1:T∣x0)q(x1:T∣x0)pθ(x0:T))≤−Eq(x0:T)logq(x1:T∣x0)pθ(x0:T)=Eq(x0:T)[logpθ(x0:T)q(x1:T∣x0)]=LVTB In order to convert each term in the equation into analytically calculable , The goal can be further rewritten into several KL The combination of divergence and entropy L T V B = E q ( x 0 : T ) [ log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] = E q [ log ∏ t = 1 T q ( x t ∣ x t − 1 ) p θ ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ p ( x t ) ) ] = E q [ − log p θ ( x T ) + ∑ t = 1 T log q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) ] = E q [ − log p θ ( x T ) + ∑ t = 2 T log q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) + log q ( x 1 ∣ x 0 ) p θ ( x 0 ∣ x 1 ) ] = E q [ − log p θ ( x T ) + ∑ t = 2 T log ( q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) ⋅ q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) ) + log q ( x 1 ∣ x 0 ) p θ ( x 0 ∣ x 1 ) ] = E q [ − log p θ ( x T ) + ∑ t = 2 T log q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + ∑ t = 2 T log q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) + log q ( x 1 ∣ x 0 ) p θ ( x 0 ∣ x 1 ) ] = E q [ − log p θ ( x T ) + ∑ t = 2 T log q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + log q ( x T ∣ x 0 ) q ( x 1 ∣ x 0 ) + log q ( x 1 ∣ x 0 ) p θ ( x ∣ x 1 ) ] = E q [ log q ( x T ∣ x 0 ) p θ ( x T ) + ∑ t = 2 T log q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) − log p θ ( x 0 ∣ x 1 ) ] = E q [ D K L ( q ( x T ∣ x 0 ) ∣ ∣ p θ ( x T ) ) + ∑ t = 2 T D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) − log p θ ( x 0 ∣ x 1 ) ] \begin{aligned}L_{\mathrm{TVB}}&=\mathbb{E}_{q({\bf{x}}_{0:T})}\left[\log \frac{q({\bf{x}}_{1:T}|{\bf{x}}_0)}{p_\theta({\bf{x}}_{0:T})}\right]\\&=\mathbb{E}_q\left[\log\frac{\prod_{t=1}^T q({\bf{x}}_t|{\bf{x}}_{t-1})}{p_\theta({\bf{x}}_T)\prod_{t=1}^T p_\theta({\bf{x}}_{t-1}|p({\bf{x}}_t))}\right]\\&=\mathbb{E}_q\left[-\log p_\theta({\bf{x}}_T)+\sum\limits_{t=1}^T\log \frac{q({\bf{x}}_t|{\bf{x}}_{t-1})}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)}\right]\\&=\mathbb{E}_q\left[-\log p_\theta({\bf{x}}_T)+\sum\limits_{t=2}^T \log\frac{q({\bf{x}}_{t}|{\bf{x}}_{t-1})}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_{t})}+\log\frac{q({\bf{x}}_1|{\bf{x}}_0)}{p_\theta({\bf{x}}_0|{\bf{x}}_1)}\right]\\&=\mathbb{E}_q\left[-\log p_\theta({\bf{x}}_T)+\sum\limits_{t=2}^T\log\left(\frac{q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)}\cdot\frac{q({\bf{x}}_t|{\bf{x}}_0)}{q({\bf{x}}_{t-1}|{\bf{x}}_0)}\right)+\log\frac{q({\bf{x}}_1|{\bf{x}}_0)}{p_\theta({\bf{x}}_0|{\bf{x}}_1)}\right]\\&=\mathbb{E}_q\left[-\log p_\theta({\bf{x}}_T)+\sum\limits_{t=2}^T\log \frac{q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)}+\sum\limits_{t=2}^T\log \frac{q({\bf{x}}_t|{\bf{x}}_0)}{q({\bf{x}}_{t-1}|{\bf{x}}_0)}+\log \frac{q({\bf{x}}_1|{\bf{x}}_0)}{p_\theta({\bf{x}}_0|{\bf{x}}_1)}\right]\\&=\mathbb{E}_q\left[-\log p_\theta({\bf{x}}_T)+\sum\limits_{t=2}^T\log \frac{q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)}+\log\frac{q({\bf{x}}_T|{\bf{x}}_0)}{q({\bf{x}}_1|{\bf{x}}_0)}+\log \frac{q({\bf{x}}_1|{\bf{x}}_0)}{p_\theta({\bf{x}}|{\bf{x}}_1)}\right]\\&=\mathbb{E}_q\left[\log \frac{q({\bf{x}}_T|{\bf{x}}_0)}{p_\theta({\bf{x}}_T)}+\sum\limits_{t=2}^T\log \frac{q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)}{p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)}-\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\right]\\&=\mathbb{E}_q\left[D_{\mathrm{KL}}(q({\bf{x}}_T|{\bf{x}}_0)||p_\theta({\bf{x}}_T))+\sum\limits_{t=2}^T D_{\mathrm{KL}}(q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)||p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t))-\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\right]\end{aligned} LTVB=Eq(x0:T)[logpθ(x0:T)q(x1:T∣x0)]=Eq[logpθ(xT)∏t=1Tpθ(xt−1∣p(xt))∏t=1Tq(xt∣xt−1)]=Eq[−logpθ(xT)+t=1∑Tlogpθ(xt−1∣xt)q(xt∣xt−1)]=Eq[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt∣xt−1)+logpθ(x0∣x1)q(x1∣x0)]=Eq[−logpθ(xT)+t=2∑Tlog(pθ(xt−1∣xt)q(xt−1∣xt,x0)⋅q(xt−1∣x0)q(xt∣x0))+logpθ(x0∣x1)q(x1∣x0)]=Eq[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+t=2∑Tlogq(xt−1∣x0)q(xt∣x0)+logpθ(x0∣x1)q(x1∣x0)]=Eq[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+logq(x1∣x0)q(xT∣x0)+logpθ(x∣x1)q(x1∣x0)]=Eq[logpθ(xT)q(xT∣x0)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)−logpθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∣∣pθ(xT))+t=2∑TDKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))−logpθ(x0∣x1)] Mark each component in the lower bound loss of variation as L V L B = L T + L T − 1 + ⋯ + L 0 L T = D K L ( q ( x T ∣ x 0 ) ∣ ∣ p θ ( x T ) ) L t = D K L ( q ( x t ∣ x t + 1 , x 0 ) ∣ ∣ p θ ( x t ∣ x t + 1 ) ) L 0 = − log p θ ( x 0 ∣ x 1 ) \begin{aligned}L_{\mathrm{VLB}}&=L_T+L_{T-1}+\cdots+L_{0}\\L_T&=D_{\mathrm{KL}}(q({\bf{x}}_T|{\bf{x}}_0)||p_\theta({\bf{x}}_T))\\L_t&=D_{\mathrm{KL}}(q({\bf{x}}_t|{\bf{x}}_{t+1},{\bf{x}}_0)||p_\theta({\bf{x}}_t|{\bf{x}}_{t+1}))\\L_0&=-\log p_\theta({\bf{x}}_0|{\bf{x}}_1)\end{aligned} LVLBLTLtL0=LT+LT−1+⋯+L0=DKL(q(xT∣x0)∣∣pθ(xT))=DKL(q(xt∣xt+1,x0)∣∣pθ(xt∣xt+1))=−logpθ(x0∣x1) L V L B L_{\mathrm{VLB}} LVLB Each of the KL term ( except L 0 L_0 L0) Measure the distance between two Gaussian distributions , Therefore, they can be calculated with closed form solutions . L T L_T LT Is constant , It can be ignored in the training process , And the reason is that q q q There are no parameters to learn and x T {\bf{x}}_T xT It's Gaussian noise , L 0 L_0 L0 It can be downloaded from N ( x 0 , μ θ ( x 1 , 1 ) , Σ θ ( x 1 , 1 ) \mathcal{N({\bf{x}}_0,\boldsymbol{\mu}_\theta({\bf{x}}_1,1),{\bf{\Sigma}}_\theta({\bf{x}}_1,1)} N(x0,μθ(x1,1),Σθ(x1,1) It's derived from .
5 Parameterization of training loss
When it is necessary to learn a neural network to approximate the conditional probability distribution in the reverse diffusion process p θ ( x t − 1 ∣ x t ) = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta({\bf{x}}_{t-1}|{\bf{x}}_t)=\mathcal{N}({\bf{x}}_{t-1};\boldsymbol{\mu}_\theta({\bf{x}}_t,t),{\bf{\Sigma}}_\theta({\bf{x}}_t,t)) pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)) when , I want to train μ θ \boldsymbol{\mu}_\theta μθ forecast μ ~ t = 1 α t ( x − β t 1 − α ˉ t z t ) \tilde{\boldsymbol{\mu}}_t=\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}{\bf{z}}_t\right) μ~t=αt1(x−1−αˉtβtzt). because x t {\bf{x}}_t xt It can be used as input during training , The Gaussian noise term can be re parameterized , So that it changes from time step t t t The input of x t {\bf{x}}_t xt Medium forecast z t {\bf{z}}_t zt:
μ θ ( x t , t ) = 1 α t ( x t − β t 1 − α ˉ t z θ ( x t , t ) ) x t − 1 = N ( x t − 1 ; 1 α t ( x t − β t 1 − α ˉ t z θ ( x t , t ) ) , Σ θ ( x t , t ) ) \begin{aligned}{\boldsymbol{\mu}}_\theta({\bf{x}}_t,t)&=\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}{\bf{z}}_\theta({\bf{x}}_t,t)\right)\\{\bf{x}}_{t-1}&=\mathcal{N}\left({\bf{x}}_{t-1};\frac{1}{\sqrt{\alpha_t}}\left({\bf{x}}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}{\bf{z}}_\theta({\bf{x}}_t,t)\right),{\bf{\Sigma}}_\theta({\bf{x}}_t,t)\right)\end{aligned} μθ(xt,t)xt−1=αt1(xt−1−αˉtβtzθ(xt,t))=N(xt−1;αt1(xt−1−αˉtβtzθ(xt,t)),Σθ(xt,t)) Loss item L t L_t Lt Is parameterized in order to minimize from μ ~ \tilde{\boldsymbol{\mu}} μ~ The difference of L t = E x 0 , z [ 1 2 ∥ Σ θ ( x t , t ) ∥ 2 2 ∥ μ ~ t ( x t , x 0 ) − μ θ ( x t , t ) ∥ 2 ] = E x 0 , z [ 1 2 ∥ Σ θ ∥ 2 2 ∥ 1 α t ( x t − β t 1 − α ˉ z ) − 1 α t ( x t − β t 1 − α ˉ z θ ( x t , t ) ) ∥ ] = E x 0 , z [ β t 2 2 α t ( 1 − α ˉ t ) ∥ Σ θ ∥ 2 2 ∥ z t − z θ ( x t , t ) ∥ 2 ] = E x 0 , z [ β t 2 2 α t ( 1 − α ˉ t ) ∥ Σ θ ∥ 2 2 ∥ z t − z θ ( α ˉ t x 0 + 1 − α ˉ t z t , t ) ∥ 2 ] \begin{aligned}L_t&=\mathbb{E}_{ {\bf{x}}_0,{\bf{z}}}\left[\frac{1}{2\|{\bf{\Sigma}}_\theta({\bf{x}}_t,t)\|_2^2}\|\tilde{\boldsymbol{\mu}}_t({\bf{x}}_t,{\bf{x}}_0)-{\boldsymbol{\mu}}_\theta({\bf{x}}_t,t)\|^2\right]\\&=\mathbb{E}_{ {\bf{x}}_0,{\bf{z}}}\left[\frac{1}{2\|{\bf{\Sigma}}_\theta\|_2^2}\left\|\frac{1}{\sqrt{\alpha}_t}\left({\bf{x}}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}}}{\bf{z}}\right)-\frac{1}{\sqrt{\alpha}_t}\left({\bf{x}}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}}}{\bf{z}}_\theta({\bf{x}}_t,t)\right)\right\|\right]\\&=\mathbb{E}_{ {\bf{x}}_0,{\bf{z}}}\left[\frac{\beta^2_t}{2\alpha_t(1-\bar{\alpha}_t)\|{\bf{\Sigma}}_\theta\|_2^2}\|{\bf{z}}_t-{\bf{z}}_\theta({\bf{x}}_t,t)\|^2\right]\\&=\mathbb{E}_{ {\bf{x}}_0,{\bf{z}}}\left[\frac{\beta^2_t}{2\alpha_t(1-\bar{\alpha}_t)\|{\bf{\Sigma}}_\theta\|_2^2}\|{\bf{z}}_t-{\bf{z}}_\theta(\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}{\bf{z}}_t,t)\|^2\right]\end{aligned} Lt=Ex0,z[2∥Σθ(xt,t)∥221∥μ~t(xt,x0)−μθ(xt,t)∥2]=Ex0,z[2∥Σθ∥221∥∥∥∥αt1(xt−1−αˉβtz)−αt1(xt−1−αˉβtzθ(xt,t))∥∥∥∥]=Ex0,z[2αt(1−αˉt)∥Σθ∥22βt2∥zt−zθ(xt,t)∥2]=Ex0,z[2αt(1−αˉt)∥Σθ∥22βt2∥zt−zθ(αˉtx0+1−αˉtzt,t)∥2] Based on experience Ho The experience of others , It is found that under the simplification goal of ignoring the weighted term , The effect of training diffusion model is better : L t s i m p l e = E x 0 , z t [ ∥ z t − z θ ( α ˉ t x 0 + 1 − α ˉ t z t , t ) ∥ 2 ] L^{\mathrm{simple}}_t=\mathbb{E}_{ {\bf{x}}_0,{\bf{z}}_t}\left[\|{\bf{z}}_t-{\bf{z}}_\theta(\sqrt{\bar{\alpha}_t}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_t}{\bf{z}}_t,t)\|^2\right] Ltsimple=Ex0,zt[∥zt−zθ(αˉtx0+1−αˉtzt,t)∥2] So the final simplified objective function is : L s i m p l e = L s i m p l e + C L_{\mathrm{simple}}=L^{\mathrm{simple}}+C Lsimple=Lsimple+C among C C C Whether it depends on θ \theta θ The constant .
6 Noise rating condition network (NCSN)
Song and Ermon Et al. Proposed a fraction based generation modeling method , The sample is passed Langevin Dynamics is generated using the gradient of data distribution estimated by fractional matching . Each sample x \bf{x} x The density probability score of is defined as its gradient ∇ x log p ( x ) \nabla_{\bf{x}}\log p({\bf{x}}) ∇xlogp(x). Train a score network s θ : R D → R D s_\theta:\mathbb{R}^D\rightarrow\mathbb{R}^D sθ:RD→RD To estimate it . In order to use high-dimensional data in deep learning settings to make it scalable , Some studies suggest using denoising score matching ( Add pre specified small noise to the data ) Or slice score matching .Langevin Dynamics can sample data points from the probability density distribution using only the fraction in the iteration process ∇ x log p ( x ) \nabla_{\bf{x}}\log p({\bf{x}}) ∇xlogp(x). However , According to the manifold hypothesis , Most of the data is expected to be concentrated in low dimensional manifolds , Even the observed data may seem to be of arbitrary high dimensions . Because data points cannot cover the whole space R D \mathbb{R}^D RD, Therefore, it has a negative impact on score estimation . In areas with low data density , The score estimation is not reliable . Add a small Gaussian noise to make the disturbed data distribution cover the whole space , The training of score evaluation network becomes more stable . Song and Ermon Et al. Improved it by disturbing data with different levels of noise , A noise condition scoring network is trained to jointly estimate the scores of all disturbed data under different noise levels .
7 β t \beta_t βt and Σ θ {\bf{\Sigma}}_\theta Σθ Parameterization of
A parameterized β t \beta_t βt In the process of ,Ho Et al. Set the forward variance as a series of linearly increasing constants , from β 1 = 1 0 − 4 \beta_1=10^{-4} β1=10−4 To β T = 0.02 \beta_T=0.02 βT=0.02. And [ − 1 , 1 ] [-1,1] [−1,1] Between normalized image pixel values , They are relatively small . Under this setting, the diffusion model in the experiment generates high-quality samples , But it still can't be competitive like other generation models .Nichol and Dhariwal Et al. Proposed several improved techniques to help the diffusion model achieve lower NLL. One of the improvements is the use of cosine based variance plans . The choice of scheduling function can be arbitrary , As long as it provides a near linear descent and surround in the middle of the training process t = 0 t=0 t=0 and t = T t=T t=T Subtle changes in β t = c l i p ( 1 − α ˉ t α t − 1 , 0.999 ) α ˉ t = f ( t ) f ( 0 ) w h e r e f ( t ) = cos ( t / T + s 1 + s ⋅ π 2 ) \beta_t=\mathrm{clip}(1-\frac{\bar{\alpha}_t}{\alpha_{t-1}},0.999)\quad \bar{\alpha}_t=\frac{f(t)}{f(0)} \quad \mathrm{where}\text{ } f(t)=\cos(\frac{t/T+s}{1+s}\cdot \frac{\pi}{2}) βt=clip(1−αt−1αˉt,0.999)αˉt=f(0)f(t)where f(t)=cos(1+st/T+s⋅2π) Among them t = 0 t=0 t=0 Small offset s s s To prevent β t \beta_t βt Too small when approaching .
A parameterized Σ θ {\bf{\Sigma}}_\theta Σθ In the process of ,Ho Others choose to fix β t \beta_t βt For constant , Instead of making them learnable and settable Σ θ ( x t , t ) = σ t 2 I {\bf{\Sigma}}_\theta({\bf{x}}_t,t)=\sigma^2_t{\bf{I}} Σθ(xt,t)=σt2I, among σ t \sigma_t σt You can't learn . The experiment found that learning diagonal variance Σ θ {\bf{\Sigma}}_\theta Σθ It will lead to unstable training and decreased sample quality .Nichol and Dhariwal Others proposed to learn Σ θ ( x t , t ) {\bf{\Sigma}}_\theta({\bf{x}}_t,t) Σθ(xt,t) As β \beta β and β ~ t \tilde{\beta}_t β~t Interpolation between , Predict the mixing vector through the model v {\bf{v}} v, Then there are : Σ θ ( x t , t ) = exp ( v log β t + ( 1 − v ) log β ~ t ) {\bf{\Sigma}}_\theta({\bf{x}}_t,t)=\exp({\bf{v}}\log \beta_t+(1-{\bf{v}})\log\tilde{\beta}_t) Σθ(xt,t)=exp(vlogβt+(1−v)logβ~t) Simple goals L s i m p l e L_{\mathrm{simple}} Lsimple It doesn't depend on Σ θ {\bf{\Sigma}}_\theta Σθ. To increase dependency , They built a hybrid goal L h y b r i d = L s i m p l e + λ L V L B L_{\mathrm{hybrid}}=L_{\mathrm{simple}}+\lambda L_{\mathrm{VLB}} Lhybrid=Lsimple+λLVLB, among λ = 0.001 \lambda=0.001 λ=0.001 It's small and stops at μ θ \boldsymbol{\mu}_\theta μθ Gradient of , In order to L V L B L_{\mathrm{VLB}} LVLB Guidance only Σ θ {\bf{\Sigma}}_\theta Σθ Learning from . Can be observed , Due to gradient noise , Optimize L V L B L_{\mathrm{VLB}} LVLB It's very difficult , Therefore, they suggest using a time averaged smoothing version of importance sampling .
8 Accelerated diffusion model sampling
By following the Markov chain of the reverse diffusion process from DDPM Generating samples is very slow , It may take one or thousands of steps . from DDPM In the sample 50000 50000 50000 Size is 32 × 32 32\times32 32×32 The image of needs about 20 20 20 Hours , But from Nvidia 2080 Ti GPU Upper GAN In less than a minute . A simple method is to run a step sampling plan , Sample and update each step , To reduce the intermediate sampling process . For the other way , Need to rewrite q σ ( x t ∣ x t , x 0 ) q_\sigma({\bf{x}}_t|{\bf{x}}_t,{\bf{x}}_0) qσ(xt∣xt,x0) To pass the required standard deviation σ t \sigma_t σt Parameterize : x t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t − 1 z t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t − 1 − σ t 2 z t + σ t z = α ˉ t − 1 x 0 + 1 − α ˉ t − 1 − σ t 2 x t − α ˉ t x 0 1 − α ˉ t + σ t z q σ ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; α ˉ t − 1 x 0 + 1 − α ˉ t − 1 − σ t 2 x t − α ˉ t x 0 1 − α ˉ t , σ t 2 I ) \begin{aligned}{\bf{x}}_{t-1}&=\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}}{\bf{z}}_{t-1}\\&=\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2_t{\bf{z}}_t}+\sigma_t{\bf{z}}\\&=\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2_t}\frac{ {\bf{x}}_t-\sqrt{\bar{\alpha}_t}{\bf{x}}_0}{\sqrt{1-\bar{\alpha}_t}}+\sigma_t{\bf{z}}\\q_\sigma&({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)=\mathcal{N}\left({\bf{x}}_{t-1};\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}-\sigma^2_t}\frac{ {\bf{x}}_t-\sqrt{\bar{\alpha}_t}{\bf{x}}_0}{1-\bar{\alpha}_t},\sigma^2_t{\bf{I}}\right)\end{aligned} xt−1qσ=αˉt−1x0+1−αˉt−1zt−1=αˉt−1x0+1−αˉt−1−σt2zt+σtz=αˉt−1x0+1−αˉt−1−σt21−αˉtxt−αˉtx0+σtz(xt−1∣xt,x0)=N(xt−1;αˉt−1x0+1−αˉt−1−σt21−αˉtxt−αˉtx0,σt2I) because q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; μ ~ ( x t , x 0 , β ~ t I ) ) q({\bf{x}}_{t-1}|{\bf{x}}_t,{\bf{x}}_0)=\mathcal{N}({\bf{x}}_{t-1};\tilde{\boldsymbol{\mu}}({\bf{x}}_t,{\bf{x}}_0,\tilde{\beta}_t{\bf{I}})) q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0,β~tI)), So there is β ~ t = σ t 2 = 1 − α ˉ t − 1 1 − α ˉ t ⋅ β t \tilde{\beta}_t=\sigma^2_t=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}\cdot \beta_t β~t=σt2=1−αˉt1−αˉt−1⋅βt Make σ t 2 = η ⋅ β ~ t \sigma^2_t=\eta \cdot \tilde{\beta}_t σt2=η⋅β~t, Then it can be adjusted to a super parameter η ∈ R + \eta\in \mathbb{R}^{+} η∈R+ To control the randomness of sampling . η = 0 \eta=0 η=0 The special situation of makes the sampling process deterministic , Such a model is named denoising diffusion implicit model (DDIM).DDIM Have the same marginal noise distribution , But the noise is definitely mapped back to the original data sample . In the process of generation , Only for a subset of diffusion steps S S S Sampling is { τ 1 , ⋯ , τ S } \{\tau_1,\cdots,\tau_S\} { τ1,⋯,τS}, The reasoning process becomes : q σ , τ ( x τ i − 1 ∣ x τ t , x 0 ) = N ( x τ i − 1 ; α ˉ t − 1 x 0 + 1 − α ˉ t − 1 − σ t 2 x τ i − α ˉ t x 0 1 − α ˉ t , σ t 2 I ) q_{\sigma,\tau}({\bf{x}}_{\tau_{i-1}}|{\bf{x}}_{\tau_t},{\bf{x}}_0)=\mathcal{N}({\bf{x}}_{\tau_{i-1}};\sqrt{\bar{\alpha}_{t-1}}{\bf{x}}_0+\sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}\frac{ {\bf{x}}_{\tau_i}-\sqrt{\bar{\alpha}_t}{\bf{x}}_0}{\sqrt{1-\bar{\alpha}_t}},\sigma^2_t{\bf{I}}) qσ,τ(xτi−1∣xτt,x0)=N(xτi−1;αˉt−1x0+1−αˉt−1−σt21−αˉtxτi−αˉtx0,σt2I) Can be observed DDIM In the case of a small number of samples, the best quality samples can be produced , and DDPM The performance is much worse with a small number of samples . Use DDIM The diffusion model can be trained to any number of forward steps , However, only a subset of steps in the generation process can be sampled . In conclusion , And DDPM comparison ,DDIM Advantages as follows :
- Use fewer steps to generate higher quality samples .
- Because the generation process is deterministic , Therefore has “ Uniformity ” attribute , This means that multiple samples with the same implicit variable as the condition should have similar high-level characteristics .
- Because of consistency ,DDIM Semantically meaningful interpolation can be carried out in implicit variables .
9 Conditional generation
stay ImageNet When training and generating models on data , Samples that are conditional on class labels are usually generated . In order to explicitly incorporate category information into the diffusion process ,Dhariwal and Nichol For noisy images x t {\bf{x}}_t xt Trained a classifier f ϕ ( y ∣ x t , t ) f_\phi(y|{\bf{x}}_t,t) fϕ(y∣xt,t), And use gradients ∇ x log f ϕ ( y ∣ x t , t ) \nabla_{ {\bf{x}}} \log f_{\phi}(y|{\bf{x}}_t,t) ∇xlogfϕ(y∣xt,t) To guide the diffusion sampling process towards the target category label y y y. Ablation diffusion model (ADM) And a model with additional classifier guidance (ADM-G) Can get the best generation model than the current (BigGAN) Better results . Besides ,Dhariwal and Nichol And so on UNet Make some changes to the architecture , It shows that... With diffusion model GAN Better performance . Model architecture modifications include greater model depth / Width 、 More attention head 、 Multiresolution attention 、 Used for the / Down sampled BigGAN Residual block 、 Residual connection rescaling and adaptive group normalization (AdaGN).
边栏推荐
- [cloud native] Devops (I): introduction to Devops and use of code tool
- [4G/5G/6G专题基础-147]: 6G总体愿景与潜在关键技术白皮书解读-2-6G发展的宏观驱动力
- Integer or int? How to select data types for entity classes in ORM
- Jenkins modifies the system time
- ViewPager2和VIewPager的区别以及ViewPager2实现轮播图
- thinkphp3.2信息泄露
- Jenkins automated email
- Mysql database index study notes
- 信息安全实验四:Ip包监视程序实现
- How to use clipboard JS library implements copy and cut function
猜你喜欢
Jmeters use
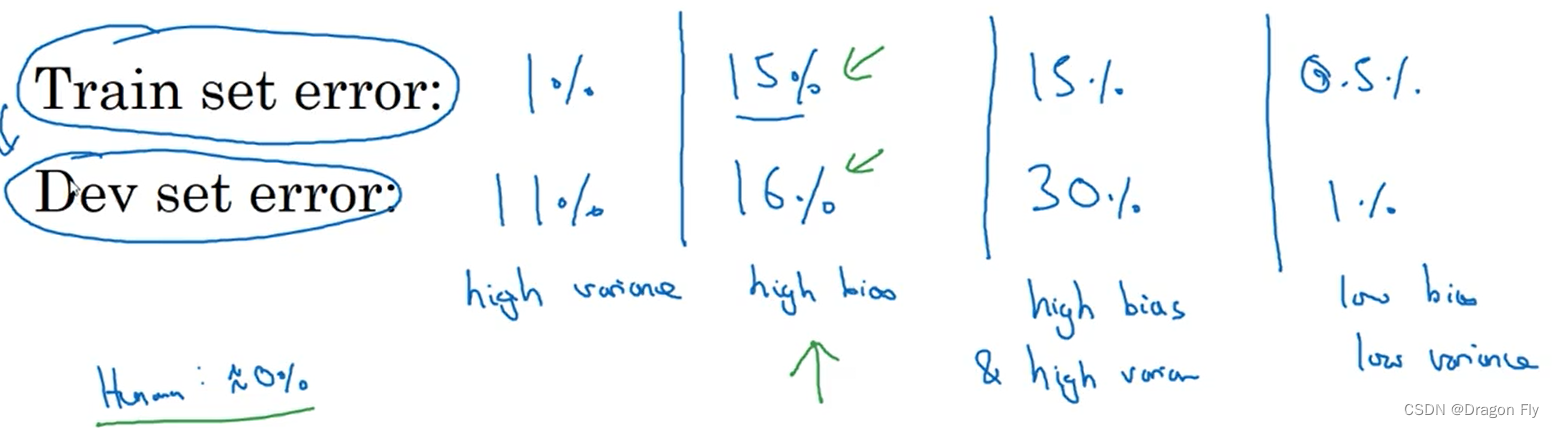
四、机器学习基础
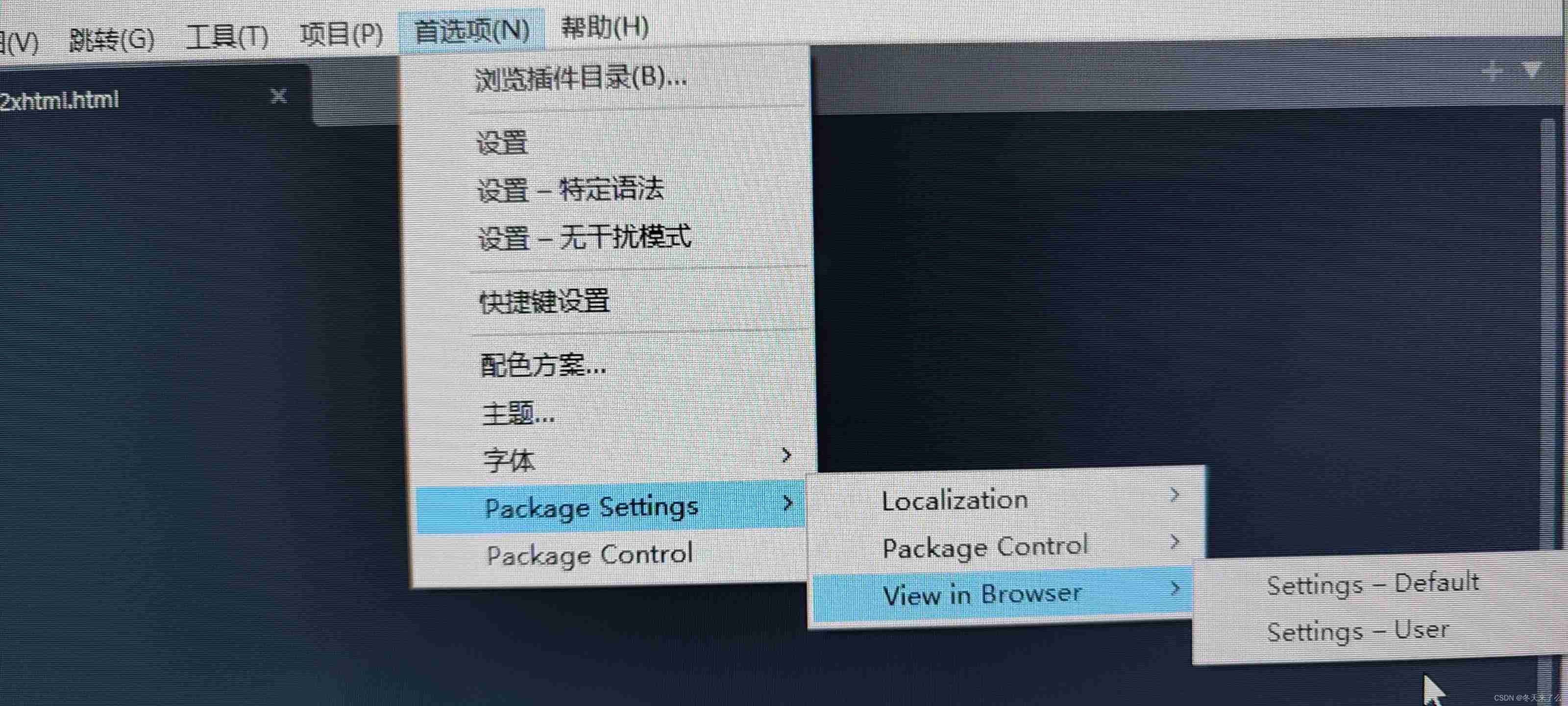
Sublime Text4 download the view in bower and set the shortcut key
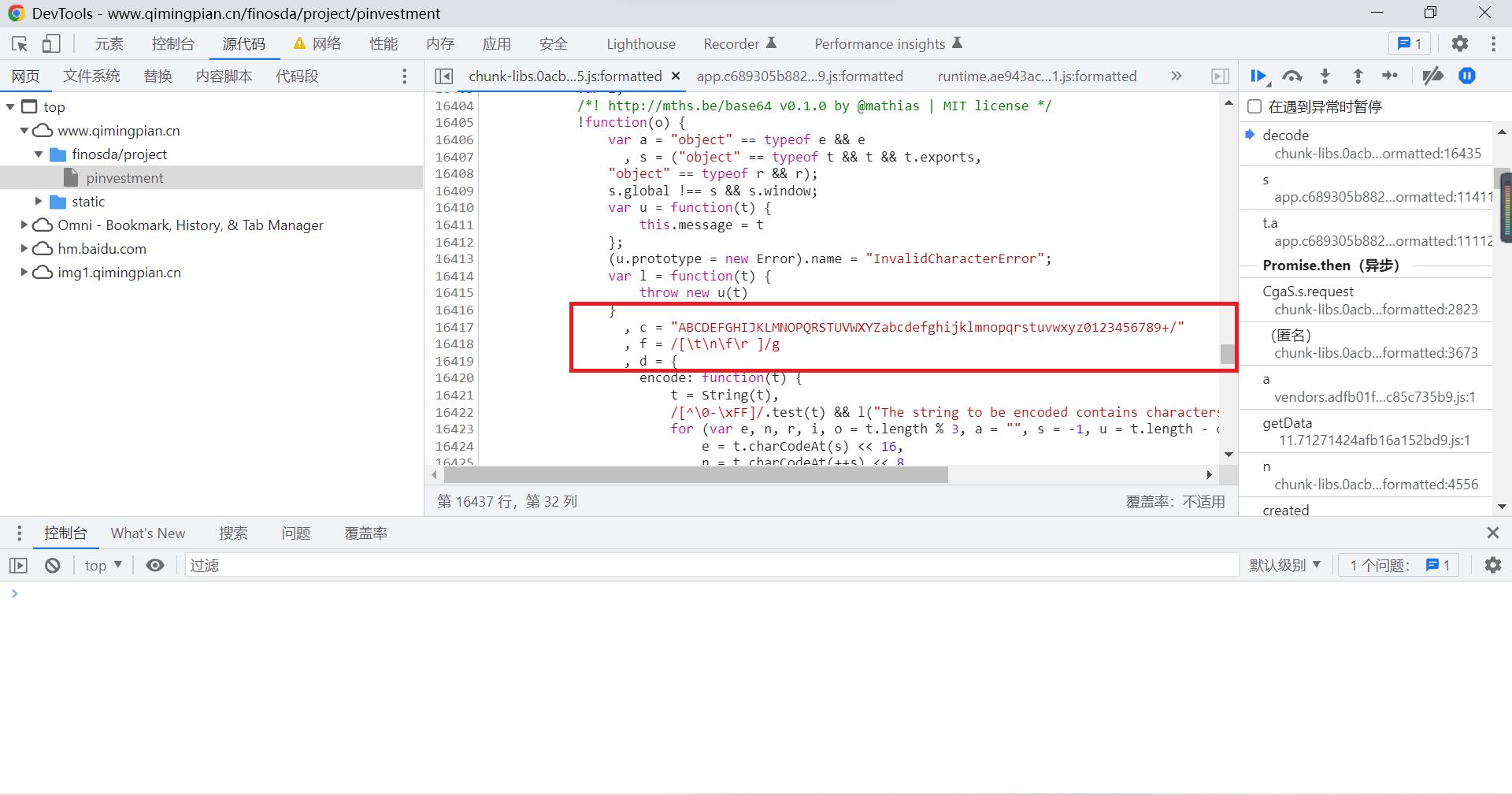
JS逆向教程第一发
![[4g/5g/6g topic foundation-146]: Interpretation of white paper on 6G overall vision and potential key technologies-1-overall vision](/img/fd/5e8f74da25d9c5f7bd69dd1cfdcd61.png)
[4g/5g/6g topic foundation-146]: Interpretation of white paper on 6G overall vision and potential key technologies-1-overall vision

Integer or int? How to select data types for entity classes in ORM
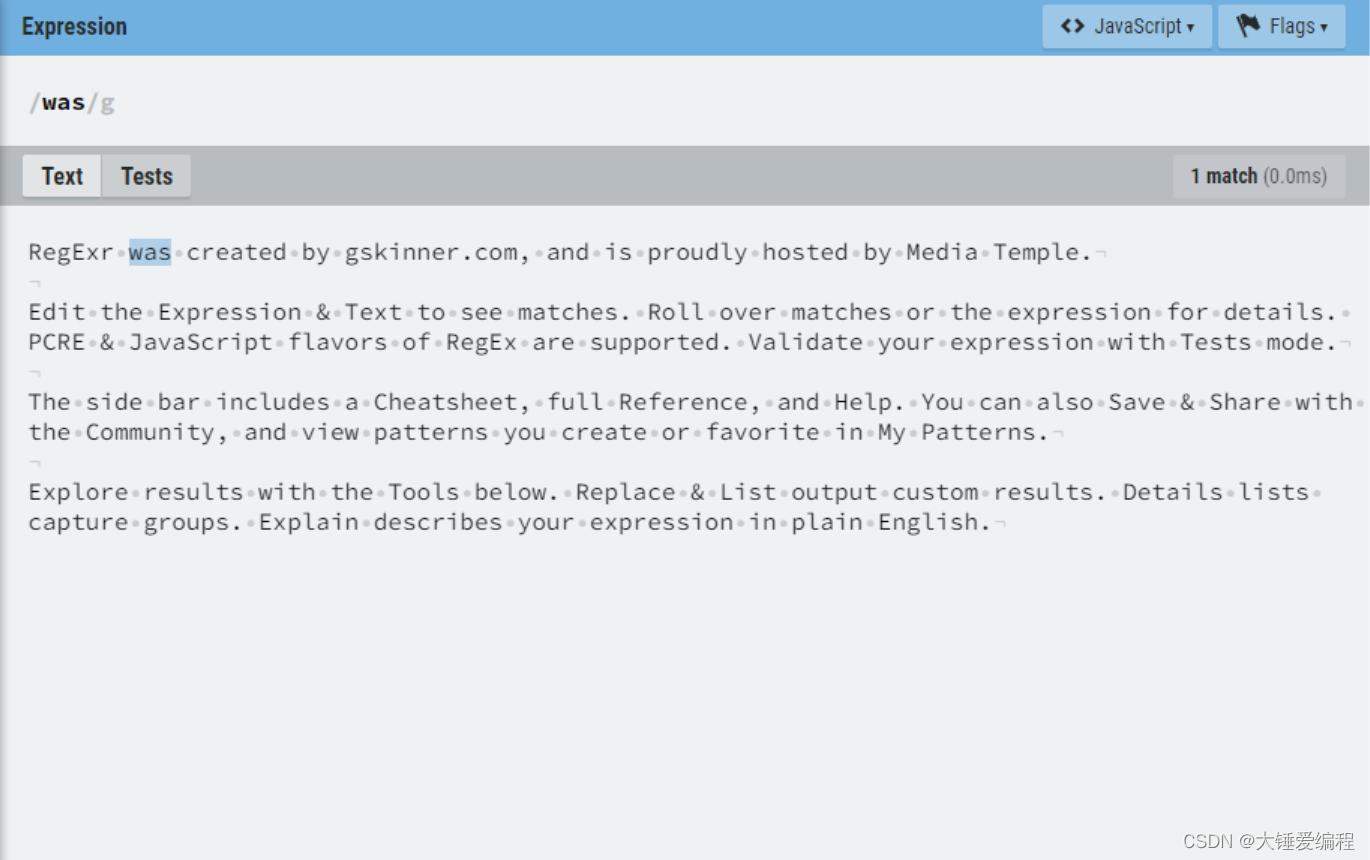
正则匹配以XXX开头的,XXX结束的
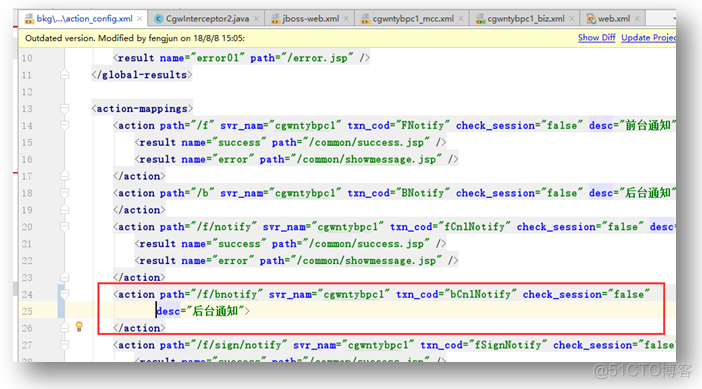
Where is the answer? action config/Interceptor/class/servlet
Unity uses mesh to realize real-time point cloud (I)

ComputeShader
随机推荐
scrapy爬虫mysql,Django等
Connecting mobile phone with ADB
**Grafana installation**
Niuke - Huawei question bank (61~70)
Variable parameter of variable length function
二叉树高频题型
Unittest simple project
How to become a senior digital IC Design Engineer (1-6) Verilog coding Grammar: Classic Digital IC Design
Where is the answer? action config/Interceptor/class/servlet
NATAPP内网穿透
JS judge whether checkbox is selected in the project
JS逆向教程第一发
[cloud native] Devops (I): introduction to Devops and use of code tool
How to solve the problem of golang select mechanism and timeout
Create an int type array with a length of 6. The values of the array elements are required to be between 1-30 and are assigned randomly. At the same time, the values of the required elements are diffe
沙龙预告|GameFi 领域的瓶颈和解决方案
Liunx command
Unity shader (basic concept)
flinkcdc 用sqlclient可以指定mysqlbinlog id执行任务吗
Oracle安装增强功能出错