当前位置:网站首页>LeetCode_Nov_4th_Week
LeetCode_Nov_4th_Week
2022-08-04 05:30:00 【KuoGavin】
November 22nd : 384. 打乱数组
November 23rd : 859. 亲密字符串
November 24th : 423. 从英文中重建数字
November 25th : 458. 可怜的小猪
November 26th : 700. 二叉搜索树中的搜索
November 27th : 519. 随机翻转矩阵
November 28th : 438. 找到字符串中所有字母异位词
November 22nd : 384. 打乱数组
① 依次从待选数字(要打乱的数组的数字)中随机选出一个,然后放入 s h u f f l e shuffle shuffle 数组的当前位置上,位置再逐次后移,同时把所选出的数字从要打乱的数组中删掉,这样遍历操作一遍即可得到等概率的打乱数组。对于原数组中的数字,移动到第 i i i 个位置的概率是 1 n \frac{1}{n} n1:
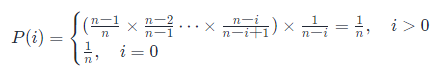
对于删掉要打乱的数组中所随机选取的元素,可采用链表的数据结构,搭配哈希表, O ( 1 ) O(1) O(1) 时间复杂度查找和删除数字。
② ①的思路可以经过整理变形,先把要打乱的数组复制为 s h u f f l e shuffle shuffle 数组,再把 s h u f f l e shuffle shuffle 数组第 i i i 个数字换至数组中的一个随机位置。也即是从排列的方式思考一下从 n ! n! n! 中选随机数的方案, n ! = n ∗ ( n − 1 ) ! n! = n * (n-1)! n!=n∗(n−1)! 这里的 n n n 就是你先挑选出第一个元素的种类数;然后 ( n − 1 ) ! (n-1)! (n−1)! 就是对其他元素的排列。所以我们要选一种洗牌方案,就可以先等概率的从 n n n 个元素中挑选一个作为第一个元素;然后再对剩下的 ( n − 1 ) (n-1) (n−1) 个元素作类似的选择。这样就相当于把 n ! n! n! 分成 n n n 段,先选择其中一段,里面有 ( n − 1 ) ! (n-1)! (n−1)! 个元素,我们把这 ( n − 1 ) ! (n-1)! (n−1)! 个情况分成 ( n − 1 ) (n-1) (n−1) 段,再随机选一个,以此类推。 这样的策略是可以做到从 ( n − 1 ) ! (n-1)! (n−1)! 中随机选数的。
//version 2②
class Solution {
public:
Solution(vector<int>& nums) {
Elements = nums;
}
vector<int> reset() {
return Elements;
}
vector<int> shuffle() {
vector<int> vShuffle = Elements;
for(int i = 1; i < vShuffle.size(); ++i) {
int r = rand() % (i + 1);
swap(vShuffle[r], vShuffle[i]);
}
return vShuffle;
}
private:
vector<int> Elements;
};
November 23rd : 859. 亲密字符串
满足以下两个条件,两字符串互为亲密字符串:
① 两字符串字符频次相同(可以使用异或的方法,在 O ( n ) O(n) O(n)时间复杂度下计算频次是否相同,但是步骤②还需要字符的频次数目,所以使用数组计数方法);
② 有两个位置两字符串对应的字符不一致,或都对应一致但是有字符的频次大于等于 2 2 2;
时间复杂度 O ( n + C ) O(n+C) O(n+C),空间复杂度 O ( C ) O(C) O(C);根据数据规模, O ( n 2 ) O(n^2) O(n2)的计算量在 4 ∗ 1 0 8 4*10^8 4∗108,要超时,暴力方法不能通过。
class Solution {
public:
bool buddyStrings(string s, string goal) {
if(s.size() != goal.size()) return false;
vector<int> cnt1 = vector<int>(26, 0);
vector<int> cnt2 = vector<int>(26, 0);
int chLocDiff = 0; //同一位置字符不同的数目
for(int i = 0; i < s.size(); ++i) {
cnt1[s[i] - 'a']++;
cnt2[goal[i] - 'a']++;
if(s[i] != goal[i]) chLocDiff++;
}
bool hasSame = false; //是否有频次大于2的字符
for(int i = 0; i < 26; ++i) {
//同一字符频次不同,直接返回假
if(cnt1[i] != cnt2[i]) return false;
if(cnt1[i] > 1) hasSame = true;
}
//频次相同,不同数目为2,
//或不同数目为0且有频次大于2字符则为真
return chLocDiff == 2 || (hasSame && chLocDiff == 0);
}
};
November 24th : 423. 从英文中重建数字
统计各个字母在不同数字当中出现的频次,一些特定的数字对应的有特定的唯一的字母,根据唯一字母数先确定这些特定数字个数,再进一步推断出剩余数字的个数。
class Solution {
public:
string originalDigits(string s) {
int dict[26] = {
0};
int nums[10] = {
0};
for(int i = 0; i < s.size(); ++i) dict[s[i]-'a']++;
nums[0] = dict['z'-'a']; //zero,只有0含字母z
nums[2] = dict['w'-'a']; //two,只有2含字母w
nums[4] = dict['u'-'a']; //four,只有4含字母u
nums[6] = dict['x'-'a']; //six,只有6含字母x
nums[8] = dict['g'-'a']; //eight,只有8含字母g
nums[3] = dict['h'-'a'] - nums[8]; //含h的只有3,8
nums[5] = dict['f'-'a'] - nums[4]; //含f的只有4,5
nums[7] = dict['v'-'a'] - nums[5]; //含v的只有5,7
nums[9] = dict['i'-'a'] - nums[5] - nums[6] - nums[8]; //含i的只有5,6,8,9,且均只含一个
nums[1] = dict['o'-'a'] - nums[0] - nums[2] - nums[4]; //含o的只有0,1,2,4,且均只含一个
string ret = "";
for(int i = 0; i < 10; ++i)
for(int j = 0; j < nums[i]; ++j)
ret += to_string(i);
return ret;
}
};
November 25th : 458. 可怜的小猪
可怜的小猪,可用 d p dp dp,最好用数学方法,可怜的小猪。
class Solution {
public:
int poorPigs(int buckets, int minutesToDie, int minutesToTest) {
int states = minutesToTest / minutesToDie + 1;
int pigs = ceil(log(buckets) / log(states));
return pigs;
}
};
November 26th : 700. 二叉搜索树中的搜索
没啥讲的,BST的概念有掌握的话,挺简单的一道题。
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while(root) {
if(root->val < val) root = root->right;
else if(root->val > val) root = root->left;
else return root;
}
return nullptr;
}
};
/******************************************************************/
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while(root && root->val != val) {
root = root->val > val ? root->left : root->right;
}
return root;
}
};
November 27th : 519. 随机翻转矩阵
- m , n m,n m,n的值可以达到 1 0 4 10^4 104,时间复杂度和空间复杂度若是使用数组来模拟的话会很高;
- 用一个哈希表来存储哪些下标的矩阵元素置为 1 1 1了,也即哈希表用来存储记录映射关系的改变情况,若是矩阵当前有 k k k个 1 1 1,那么 m p mp mp的 [ m ∗ n − k , m ∗ n ) [m*n-k,m*n) [m∗n−k,m∗n)范围的键值对应的映射关系为实际的置为 1 1 1的矩阵下标位置;
- 随机下标的取值范围在 [ 0 , m ∗ n − k ) [0,m*n-k) [0,m∗n−k)范围,随着 k k k( 1 1 1的个数)越来越多,也意味着范围在不断缩小,在该范围内取一哈希下标,并映射到实际的矩阵当中,再将映射置换到 m ∗ n − k − 1 m*n-k-1 m∗n−k−1的位置,同时用哈希表进行记录映射关系的改变情况,这样就可以保证范围内映射到的矩阵下标的元素值均为 0 0 0;
- 这样空间复杂度和 f i l p filp filp次数成正比,也即是 O ( F ) O(F) O(F), F F F是次数,详情见:随机翻转矩阵;
class Solution {
public:
Solution(int m, int n) : m(m), n(n) {
total = m * n;
}
vector<int> flip() {
vector<int> ret;
//0到total-1当中取一等概率随机数
int x = rand() % total;
total--;
//判断x是否是已经更改过映射关系,是则取mp中真实值,不是则映射关系未曾变化
if(mp.count(x)) ret = {
mp[x]/m, mp[x]%n};
else ret = {
x/m, x%n};
//更新x的映射关系,将其和total(m*n-k-1)的位置进行调换
//如果边界值已经在mp里,则改为真实映射值,若不在,则直接更改
if(mp.count(total)) mp[x] = mp[total];
else mp[x] = total;
return ret;
}
void reset() {
total = r*c;
mp.clear();
}
private:
int m, n;
int total;
// 记录哪些被选中的点,而且指向它没被选中的数值,可以用来输出
unordered_map<int, int> mp;
};
November 28th : 438. 找到字符串中所有字母异位词
滑动窗口,统计字符串字母频次并比照。异或方法同样不能够解决偶数次频次只有一个字母的串的匹配。
//异或的错误版本,若是碰见类如"aa","bb"这种就会判断相同了
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
if(p.size() == 0) return {
};
int winXor = 0, pXor = 0;
for(int i = 0; i < p.size(); ++i) {
winXor ^= s[i];
pXor ^= p[i];
}
vector<int> ret;
if(winXor == pXor) ret.push_back(0);
for(int i = 1; i <= s.size()-p.size(); ++i) {
//cout << i << endl;
winXor ^= s[i-1];
winXor ^= s[i+p.size()-1];
if(winXor == pXor) ret.push_back(i);
}
return ret;
}
};
/*************************************************************************************/
//version1 使用固定大小的数组来存储各个字母的频次,空间复杂度一定
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
if(s.size() < p.size()) return {
};
int l = 0, r = -1;
vector<int> freq_s(26, 0), freq_p(26, 0), res;
// 初始化代码值
for(int i = 0; i < p.size(); i++){
freq_p[p[i]-'a']++;
freq_s[s[++r]-'a']++;
}
if(freq_s == freq_p) res.push_back(l);
// 固定长度的滑动窗口
while(r < s.size()-1){
freq_s[s[++r]-'a']++;
freq_s[s[l++]-'a']--;
if(freq_s == freq_p) res.push_back(l);
}
return res;
}
};
/*************************************************************************************/
//version2 使用map来存储窗口和p的字母频次,对比时只需要把map遍历一遍即可,更省空间和时间(看取用效率)
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
if(p.size() > s.size()) return {
};
map<char, pair<int, int>> mp;
for(int i = 0; i < p.size(); ++i) {
mp[s[i]].first++;
mp[p[i]].second++;
}
vector<int> ret;
bool flag = true;
for(int i = 0; i < s.size()-p.size(); ++i) {
for(auto it = mp.begin(); it != mp.end(); ++it) {
if(it->second.first != it->second.second) {
flag = false;
break;
}
}
if(flag) ret.push_back(i);
else flag = true;
mp[s[i]].first--;
mp[s[i+p.size()]].first++;
}
for(auto it = mp.begin(); it != mp.end(); ++it) {
if(it->second.first != it->second.second) {
flag = false;
break;
}
}
if(flag) ret.push_back(s.size()-p.size());
return ret;
}
};
边栏推荐
- 典型CCN网络——efficientNet(2019-Google-已开源)
- 亚马逊云科技Build On-Amazon Neptune基于知识图谱的推荐模型构建心得
- 代码庆端午--粽你心意
- AWS使用EC2降低DeepRacer的训练成本:DeepRacer-for-cloud的实践操作
- The second official example analysis of the MOOSE platform - about creating a Kernel and solving the convection-diffusion equation
- MFC读取点云,只能正常显示第一个,显示后面时报错
- Code to celebrate the Dragon Boat Festival - Zongzi, your heart
- 投稿相关
- (Navigation page) OpenStack-M version - manual construction of two nodes - with video from station B
- 【论文阅读】Multi-View Spectral Clustering with Optimal Neighborhood Laplacian Matrix
猜你喜欢
动手学深度学习_多层感知机

MOOSE平台官方第二个例子分析——关于创建Kernel,求解对流扩散方程

MNIST Handwritten Digit Recognition - Image Analysis Method for Binary Classification
makefile基础学习
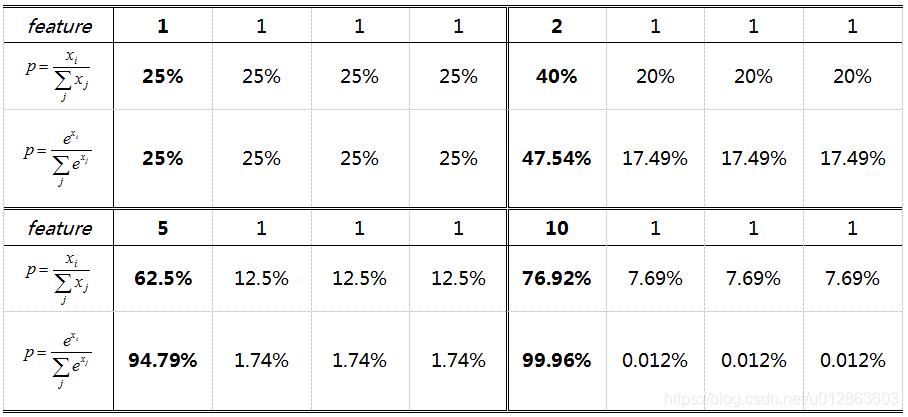
度量学习(Metric learning)—— 基于分类损失函数(softmax、交叉熵、cosface、arcface)
Vision Transformer 论文 + 详解( ViT )
【Copy攻城狮日志】飞浆学院强化学习7日打卡营-学习笔记

深度学习理论 —— 初始化、参数调节

中国联通、欧莱雅和钉钉都在争相打造的秘密武器?虚拟IP未来还有怎样的可能
Pytest常用插件
随机推荐
fuser 使用—— YOLOV5内存溢出——kill nvidai-smi 无pid 的 GPU 进程
关于DG(域泛化)领域的PCL方法的代码实例
tensorRT5.15 使用中的注意点
(TensorFlow) - detailed explanation of tf.variable_scope and tf.name_scope
Pytest常用插件
Attention Is All You Need(Transformer)
PCL窗口操作
Qt日常学习
BatchNorm&&LayerNorm
Cut the hit pro subtitles export of essays
Endnote编辑参考文献
MNIST手写数字识别 —— Lenet-5首个商用级别卷积神经网络
YOLOV4流程图(方便理解)
[CV-Learning] Convolutional Neural Network Preliminary Knowledge
No matching function for call to 'RCTBridgeModuleNameForClass'
Rules.make-适合在编辑模式下看
【论文阅读】SPANET: SPATIAL PYRAMID ATTENTION NETWORK FOR ENHANCED IMAGE RECOGNITION
动手学深度学习_卷积神经网络CNN
图像线性融合
TensorFlow2 study notes: 8. tf.keras implements linear regression, Income dataset: years of education and income dataset